
- •Механика
- •Механика
- •Оглавление
- •Предисловие
- •Введение
- •Глава 1. Кинематика
- •Механическое движение
- •1.2. Некоторые сведения о векторах
- •1.3. Скорость
- •1.4. Ускорение
- •1.5. Угловая скорость и угловое ускорение
- •Глава 2. Динамика материальной точки
- •2.1. Первый закон Ньютона. Инерциальные системы отсчета
- •2.2. Второй закон Ньютона
- •2.3. Третий закон Ньютона
- •2.4. Сила. Силы трения
- •2.5. Импульс. Закон сохранения импульса
- •2.6. Центр масс. Движение тела переменной массы
- •Глава 3. Работа и энергия
- •3.1. Понятие о работе и энергии. Мощность. Консервативные
- •Кинетическая энергия
- •Потенциальная энергия
- •Закон сохранения механической энергии
- •Графическое представление энергии.
- •3.6. Применение законов сохранения энергии и импульса
- •Используя (3.32), получаем
- •Движение в центральном поле сил
- •Глава 4. Механика твердого тела
- •4.1. Движение твердого тела
- •4.2. Момент силы
- •4.3. Центр масс твердого тела и его движение
- •4.4. Момент импульса и закон его сохранения
- •4.5. Основное уравнение динамики вращательного движения
- •4.6. Момент инерции
- •4.7. Кинетическая энергия твердого тела
- •4.7.1. Вращение тела вокруг неподвижной оси
- •4.7.2. Работа внешних сил при вращении твердого тела
- •4.7.3. Кинетическая энергия тела при плоском движении
- •Глава 5. Тяготение. Неинерциальные системы
- •5.1. Развитие представлений о природе тяготения
- •5.2. Законы Кеплера. Закон всемирного тяготения
- •5.3. Гравитационное поле и его характеристики
- •5.4. Сила тяжести и вес. Невесомость
- •5.5. Космические скорости
- •5.6. Неинерциальные системы отсчета. Силы инерции
- •5.6.1. Силы инерции при ускоренном поступательном
- •5.6.2. Центробежная сила инерции
- •5.6.3. Сила Кориолиса
- •Глава 6. Элементы механики сплошных сред
- •6.1. Гидроаэростатика
- •6.1.1. Давление
- •6.1.2. Распределение давления в покоящихся жидкости и газе
- •6.1.3. Выталкивающая сила
- •6.2. Гидроаэродинамика
- •6.2.1. Линии и трубки тока. Неразрывность струи
- •6.2.2. Уравнение Бернулли
- •6.2.3. Измерение давления в текущей жидкости
- •6.2.4. Применение к движению жидкости закона сохранения
- •6.2.5. Силы внутреннего трения
- •6.2.6. Ламинарное и турбулентное течение
- •6.2.7. Движение тел в жидкостях и газах
- •6.2.8. Подъемная сила
- •Глава 7. Элементы специальной теории
- •7.1. Принцип относительности Галилея.
- •7.2. Постулаты специальной теории относительности
- •7.3. Преобразования Лоренца
- •7.4. Следствия из преобразований Лоренца
- •7.4.1. Одновременность событий в разных системах отсчета
- •7.4.2. Длительность событий в разных системах отсчета
- •7.4.3. Длина тел в разных системах отсчета
- •7.4.4. Релятивистский закон сложения скоростей
- •7.5. Интервал между событиями
- •7.6. Релятивистская динамика. Релятивистский импульс
- •7.7. Закон взаимосвязи массы и энергии
- •7.7.1. Кинетическая энергия релятивистской частицы
- •7.7.2. Закон взаимосвязи массы и энергии
- •7.7.3. Связь между энергией и импульсом частицы
- •Глава 8. Свободные гармонические колебания
- •8.1. Гармонические колебания и их характеристика
- •8.2. Механические гармонические колебания
- •8.3. Гармонический осциллятор. Пружинный, математический
- •8.4. Графическое изображение гармонических колебаний.
- •8.5. Сложение колебаний одинакового направления
- •8.6. Сложение взаимно перпендикулярных колебаний
- •Глава 9. Свободные Затухающие колебания
- •9.1. Дифференциальное уравнение свободных затухающих
- •9.2. Основные характеристики затухающих колебаний
- •Глава 10. Вынужденные колебания
- •10.1. Дифференциальное уравнение вынужденных колебаний
- •10.2. Решение дифференциального уравнения вынужденных
- •10.3. Резонанс. Примеры резонансных явлений
- •Глава 11. Волны в упругой среде
- •11.1. Упругие волны
- •11.2. Уравнение плоской и сферической волн
- •11.3. Уравнение плоской волны, распространяющейся
- •11.4. Волновое уравнение
- •11.5. Скорость распространения упругих волн
- •11.6. Энергия упругой волны
- •11.6.1. Плотность энергии упругой волны
- •11.6.2. Плотность потока энергии
- •11.7. Стоячие волны
- •11.7.1. Уравнение стоячей волны
- •11.7.2. Энергия стоячей волны
- •11.8. Эффект Доплера для звуковых волн
- •Литература
- •Механика
- •302020, Г. Орел, Наугорское шоссе, 29.
6.2.8. Подъемная сила
Для возникновения подъемной силы вязкость жидкости не имеет существенного значения. На рис. 6.23 показаны линии тока при обтекании идеальной жидкостью полуцилиндра.

Рис. 6.23. Линии тока при обтекании
идеальной жидкостью полуцилиндра
Вследствие
полного обтекания линии тока будут
симметричны относительно прямой СD.
Однако
относительно прямой АВ
картина
будет несимметричной. Линии тока
сгущаются вблизи точки С,
поэтому
давление здесь будет меньше, чем вблизи
точки D,
и
возникает подъемная сила
![]() .
Аналогичным образом возникает подъемная
сила и в вязкой жидкости. Силой,
поддерживающей самолет в воздухе, служит
подъемная сила, действующая на его
крылья. Лобовое сопротивление играет
при полете самолета вредную роль. Поэтому
крыльям самолета и его фюзеляжу придают
хорошо обтекаемую форму. Профиль крыла
должен вместе с тем обеспечивать
достаточную по величине подъемную силу.
Оптимальным для крыла является показанный
на рис. 6.24 профиль, найденный великим
русским ученым Н.Е.
Жуковским
(1847—1921).
.
Аналогичным образом возникает подъемная
сила и в вязкой жидкости. Силой,
поддерживающей самолет в воздухе, служит
подъемная сила, действующая на его
крылья. Лобовое сопротивление играет
при полете самолета вредную роль. Поэтому
крыльям самолета и его фюзеляжу придают
хорошо обтекаемую форму. Профиль крыла
должен вместе с тем обеспечивать
достаточную по величине подъемную силу.
Оптимальным для крыла является показанный
на рис. 6.24 профиль, найденный великим
русским ученым Н.Е.
Жуковским
(1847—1921).

Рис. 6.24. Оптимальный профиль крыла самолета
Трудами Н.Е. Жуковского и его ученика С.А. Чаплыгина положено начало современной аэродинамики. Н.Е. Жуковский является отцом русской авиации, он, в частности, вывел формулу для определения подъемной силы, которая является основой всех аэродинамических расчетов самолетов.
Глава 7. Элементы специальной теории
ОТНОСИТЕЛЬНОСТИ.
РЕЛЯТИВИСТСКАЯ МЕХАНИКА
7.1. Принцип относительности Галилея.
Классическая механика. Границы применимости
Пусть имеется несколько систем отсчета, которые движутся равномерно и прямолинейно относительно друг друга. Если в одной из систем справедливы законы динамики Ньютона, то все эти системы являются инерциальными. Механический принцип относительности (принцип относительности Галилея) утверждает, что законы классической динамики имеют одинаковую форму во всех инерциальных системах отсчета.
Для доказательства рассмотрим две системы отсчета, движущиеся с постоянной скоростью v0 относительно друг друга (рис. 7.1). Будем условно считать одну из систем неподвижной. Обозначим ее К. В этом случае система К/ будет двигаться равномерно и прямолинейно относительно системы К. Выберем координатные оси x, y, z системы К и оси x/, y/, z/ системы К/ таким образом, чтобы оси x и x/ совпадали, а оси y и y/ , z и z/ были параллельны друг другу.
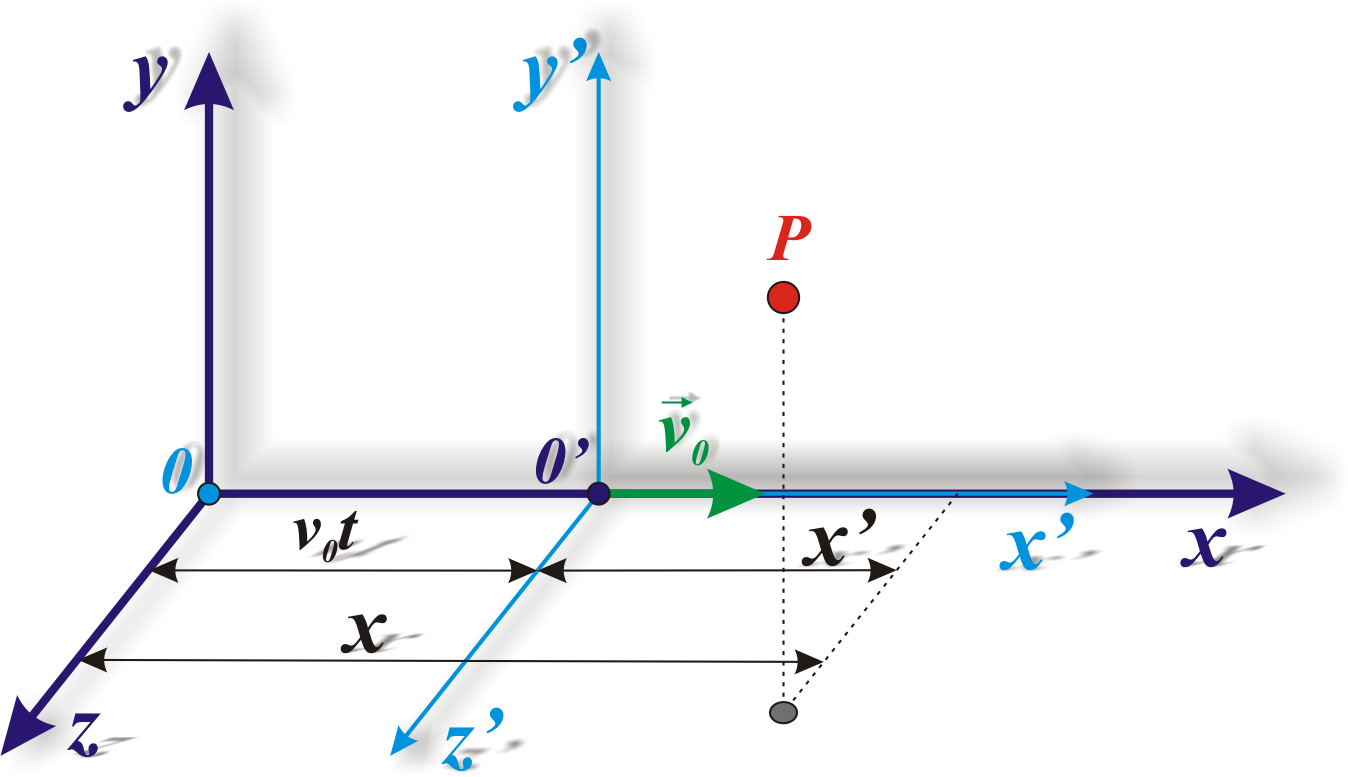
Рис. 7.1. Две системы отсчета:
К –
неподвижная и К/
‑ подвижная, движущаяся с постоянной
скоростью
![]()
Найдем координаты точки Р в обеих системах. Пусть в начальный момент времени (t = 0) начала координат систем совпадают. Из рис. 7.1 видно, что x = x/ + υ0t , y = y/ , z = z/. Учитывая, принятое в классической механике предположение, что время в обеих системах течет одинаково (t = t/), получаем совокупность четырех уравнений:
 (7.1)
(7.1)
Эти уравнения называют преобразованиями Галилея.
Продифференцировав соотношения (7.1) по времени, найдем связь между скоростями точки Р в системах отсчета К и К/:
 (7.2)
(7.2)
Скалярные соотношения (7.2) можно заменить векторным равенством:
![]() .
(7.3)
.
(7.3)
Формулы (7.2) и (7.3) представляют собой правило сложения скоростей в классической механике. При этом формула (7.3) справедлива при произвольном выборе взаимных направлений координатных осей систем К и К/, а формулы (7.1) и (7.2) выполняются только при выборе осей, показанном на рис. 7.1.
Продифференцировав
по времени соотношение (7.3) и учитывая,
что
![]() постоянна, найдем ускорение точки Р
в системе К:
постоянна, найдем ускорение точки Р
в системе К:
![]() ,
,
т.е. ускорение точки Р в системах К и К/, движущихся равномерно и прямолинейно относительно друг друга, одинаково:
![]() .
(7.4)
.
(7.4)
Если
на точку Р
не действуют другие тела (![]() ),
то, согласно (7.4) и
),
то, согласно (7.4) и
![]() .
Следовательно, система К/
является инерциальной (точка относительно
этой системы движется прямолинейно и
равномерно или покоится).
.
Следовательно, система К/
является инерциальной (точка относительно
этой системы движется прямолинейно и
равномерно или покоится).
Учитывая выражение (7.4), можно утверждать, что силы, действующие на тело в системах К и К/, будут одинаковы. Из этого следует, что уравнения динамики не изменяются при переходе от одной инерциальной системы отсчета к другой, т.е. инвариантны по отношению к преобразованию координат при переходе между инерциальными системами координат.
Все инерциальные системы отсчета эквивалентны. Это проявляется в том, что никакими опытами, проведенными в данной системе отсчета, нельзя проверить находится ли система в состоянии покоя или равномерного и прямолинейного движения.
Теория относительности Эйнштейна (1879-1955) установила границы применимости классической механики: механика Ньютона не может быть применена движению, происходящему со скоростью близкой к скорости света в вакууме. В специальной теории относительности подверглись радикальному пересмотру ньютоновские представления о пространстве и времени. Этот пересмотр привел к созданию релятивистской механики – “механики больших скоростей”. Однако новая механика не привела к полному отрицанию старой классической механики. Уравнения релятивистской механики в пределе (для скоростей, малых по сравнению со скоростью света) переходят в уравнения классической механики. Таким образом, классическая механика вошла в релятивистскую механику как ее частный случай и сохранила свое прежнее значение для описания движений, происходящих со скоростями, значительно меньшими скорости света.
Аналогично обстоит дело и с соотношением между классической и квантовой механикой. Уравнения квантовой механики также дают в пределе (для масс больших по сравнению с массами атомов) уравнения классической механики. Следовательно, классическая механика вошла и в квантовую механику в качестве ее предельного случая.
Таким образом, развитие науки не перечеркнуло классическую механику, а лишь показало ее ограниченную применимость. Классическая механика, основывающаяся на законах Ньютона, является механикой тел больших (по сравнению с массой атомов) масс, движущихся с малыми (по сравнению со скоростью света) скоростями.
