6.2.6. Ламинарное и турбулентное течение

Наблюдается два вида течения жидкости (или газа). В одних случаях жидкость как бы разделяется на слои, которые скользят друг относительно друга, не перемешиваясь. Такое течение называется ламинарным (слоистым). Если в ламинарный поток ввести подкрашенную струйку, то она сохраняется, не размываясь, на всей длине потока, так как частицы жидкости в ламинарном потоке не переходят из одного слоя в другой. Ламинарное течение стационарно.

При увеличении скорости или поперечных размеров потока характер течения существенным образом изменяется. Возникает энергичное перемешивание жидкости. Такое течение называется турбулентным. При турбулентном течении скорость частиц в каждом данном месте все время изменяется беспорядочным образом — течение нестационарно. Если в турбулентный поток ввести окрашенную струйку, то уже на небольшом расстоянии от места ее введения окрашенная жидкость равномерно распределяется по всему сечению потока.

Показанный на рис. 6.18а характер изменения скорости течения с расстоянием от оси трубы относится к случаю ламинарного течения. Таким образом, при ламинарном течении скорость изменяется с расстоянием от оси трубы по параболическому закону.

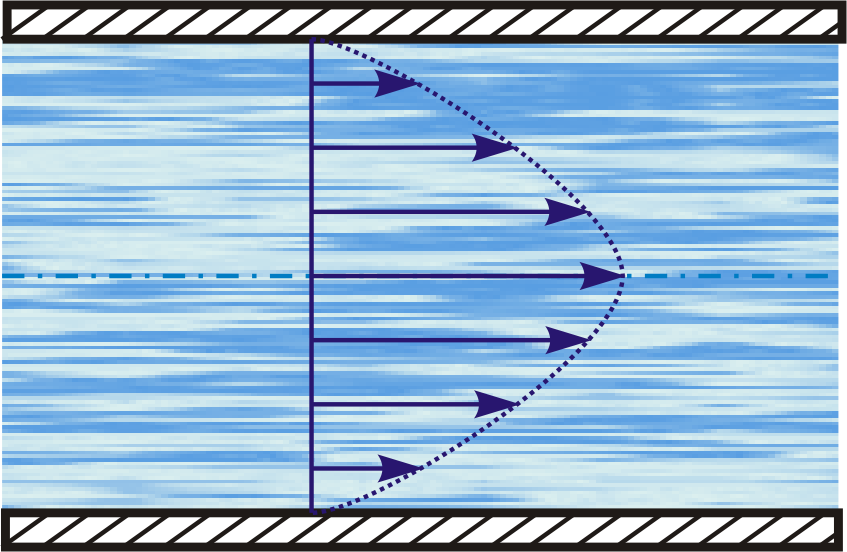
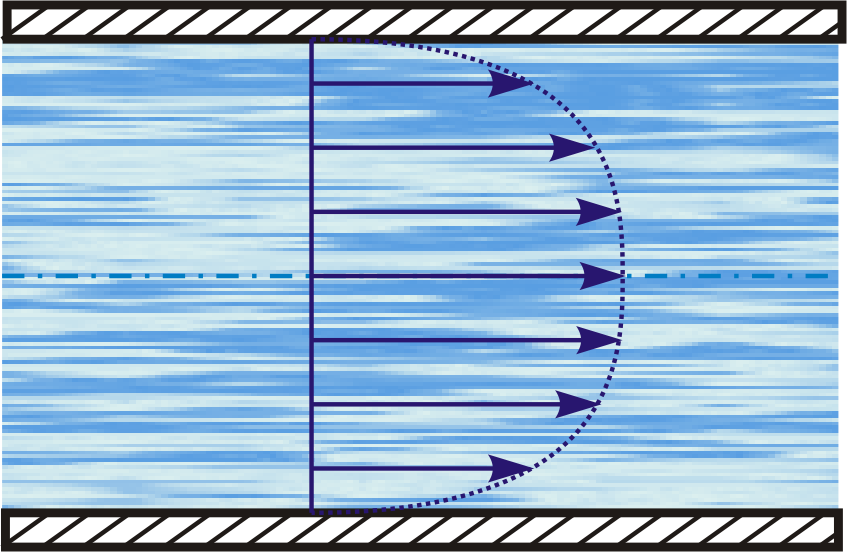
− а − б

Рис. 6.18. Ламинарное и турбулентное течения жидкости:

а - ламинарное, б - турбулентное

При турбулентном течении можно говорить о среднем (по времени) значении скорости в каждой точке сечения трубы. “Профиль” средних скоростей при турбулентном течении изображен на рис. 6.18б. Вблизи стенок трубы скорость изменяется гораздо сильнее, чем при ламинарном течении, но в остальной части сечения скорость изменяется меньше.

Английский ученый Рейнольдс установил, что характер течения зависит от значения безразмерной величины:

= , (6.23)

где ρ − плотность жидкости (или газа); ν − средняя (по сечению трубы) скорость потока; η — коэффициент вязкости жидкости; ℓ — характерный для поперечного сечения размер, например, сторона квадрата при квадратном сечении, радиус или диаметр при круглом сечении и т.п.

Величина (6.23) называется числом Рейнольдса. При малых значениях числа Рейнольдса наблюдается ламинарное течение. Начиная с некоторого определенного значения Re, называемого критическим, течение приобретает турбулентный характер. Если в качестве характерного размера для круглой трубы взять ее радиус, r то критическое значение числа Рейнольдса (которое в этом случае имеет вид =) оказывается равным примерно 1000. В число Рейнольдса входят в виде отношения две величины, зависящие от свойств жидкости: плотность и коэффициент вязкости . Отношение

(6.24)

называется кинематической вязкостью. В отличие от величина называется динамической вязкостью. Используя кинематическую вязкость, числу Рейнольдса можно придать следующий вид:

Число Рейнольдса может служить критерием подобия для течения жидкостей в трубах, каналах и т.д. Характер течения различных жидкостей (или газов) в трубах разных сечений будет совершенно одинаков, если каждому течению соответствует одно и то же значе-ние .