6.2.3. Измерение давления в текущей жидкости

В предыдущем параграфе мы выяснили, что давление в жидкости связано с величиной скорости течения. Введение в жидкость прибора для измерения давления нарушает характер движения жидкости, а следовательно, может изменить и величину измеряемого давления. Поместим в жидкость изогнутую манометрическую трубку с входным отверстием, обращенным навстречу потоку (рис. 6.12). Такую трубку называют трубкой Пито.

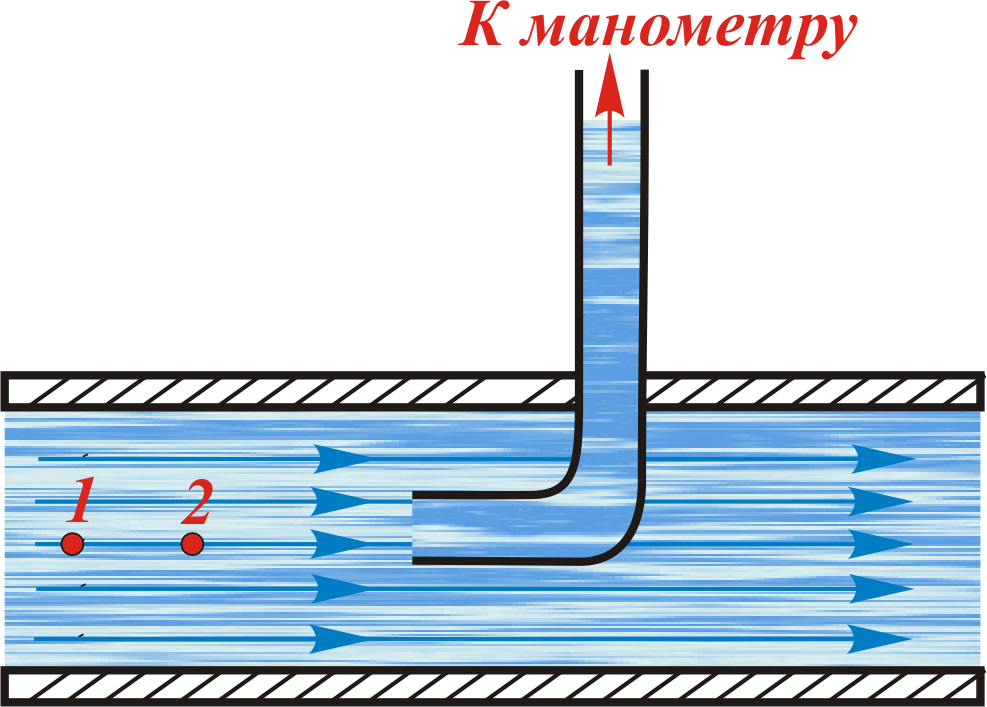
Рис. 6.12. Измерение давления в текущей

жидкости с помощью трубки Пито

Рассмотрим линию тока, упирающуюся своим концом в центр отверстия трубки. Скорость вдоль рассматриваемой линии тока будет изменяться от значения для невозмущенного потока (на больших расстояниях от трубки) до нуля непосредственно перед отверстием. Напишем уравнение Бернулли для точек 1 и 2 упирающейся в отверстие линии тока с учетом, что

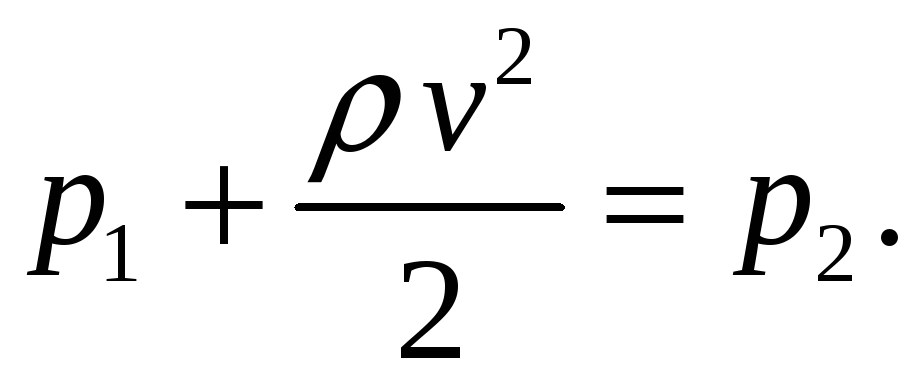
Здесь равно давлению в невозмущенном потоке, равно давлению, измеренному манометром. Следовательно, манометр, соединенный с трубкой Пито, покажет давление, равное

=. (6.16)

Слагаемое называют динамическим давлением. Давление в невозмущенном потоке называют статическим. Давление , равное сумме статического и динамического давлений, называют полным давлением. Таким образом, с помощью трубки Пито, можно измерить полное давление (6.16).

Если в тонкой изогнутой трубке сделать боковые отверстия, то скорость (а, следовательно, и давление) вблизи таких отверстий будет мало отличаться от скорости (и давления) невозмущенного потока (рис. 6.13). Поэтому манометр, присоединенный к такой трубке, называемой зондом, покажет статическое давление в жидкости р.

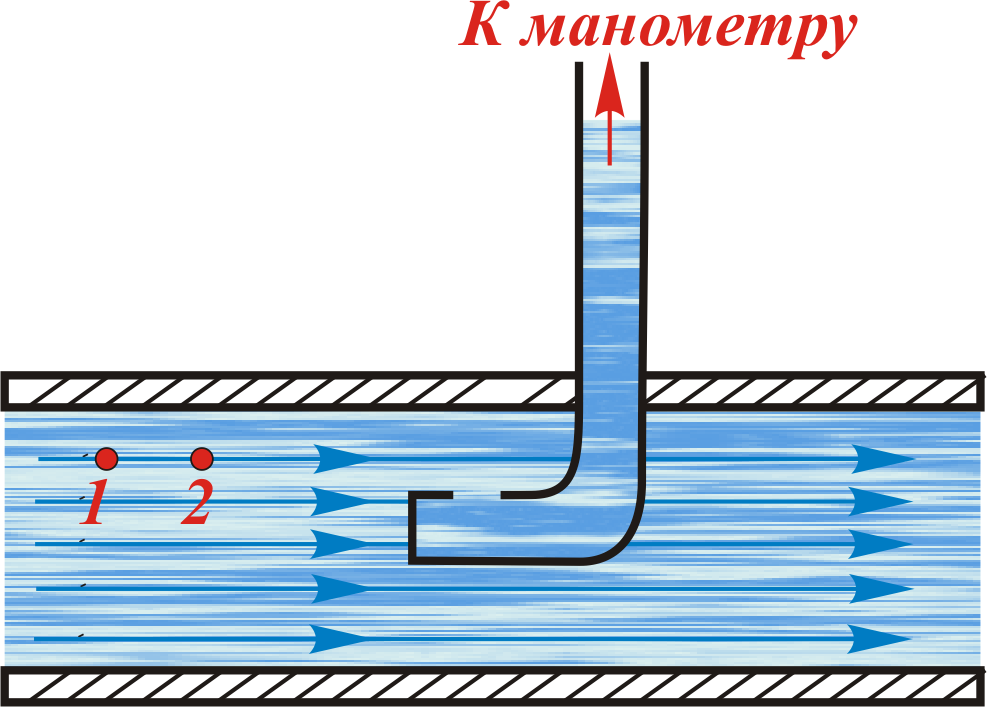
Рис. 6.13. Зонд для измерения статического давления

Зная полное и статическое давления, можно найти динамическое давление, а, следовательно, и скорость течения жидкости (плотность жидкости предполагается известной).

Если трубку Пито и зонд смонтировать вместе, как показано на рис. 6.14, и подсоединить к разным коленам дифференциальный манометр (т.е. манометр, измеряющий разность давлений), то показания манометра будут непосредственно давать динамическое давление.

Рис. 6.14. Трубка для измерения динамического давления

Проградуировав манометр в значениях скорости , можно получить прибор для измерения скорости течения жидкости.

6.2.4. Применение к движению жидкости закона сохранения

импульса

К жидкостям и газам, как и к другим телам, применим закон сохранения импульса. Используем этот закон для решения некоторых задач.

Реакция текущей жидкости на стенки изогнутой трубы

Предположим, что в изогнутой трубе установился стационарный поток несжимаемой жидкости (рис. 6.15). Возьмем трубу постоянного сечения . Тогда в силу неразрывности струи скорость в каждом сечении будет одинакова по величине и равна .

Рис. 6.15. Струя жидкости, вытекающая из трубы,

уносит с собой импульс, этот импульс сообщается

вытекающей жидкости сосудом

Рассмотрим объем изогнутого участка трубы, ограниченного сечениями и . За время ∆t в этот объем будет втекать через сечение количество жидкости , обладающее импульсом , где - вектор скорости жидкости, протекающей через сечение . Одновременно из этого объема будет вытекать через сечение такое же количество жидкости, обладающее импульсом . Таким образом, стенки изогнутого участка трубы сообщают за время текущей мимо них жидкости изменение импульса . Пусть сечение трубы постоянно, т.е. ==, тогда и для изменения импульса получим:

=.

Как мы знаем, изменение импульса тела за единицу времени равно действующей на тело силе. Следовательно, стенки трубы действуют на жидкость с силами, равнодействующая которых равна:

.

По третьему закону Ньютона текущая жидкость действует на стенки трубы с силами, равнодействующая которых равна:

. (6.17)

Силу называют реакцией текущей жидкости на стенки трубы – реакция вытекающей струи.

Таким образом, жидкость, текущая по изогнутой трубе, действует на трубу с силой реакции , направленной в сторону, противоположную, направлению изгиба трубы.

Струя жидкости, вытекающая из отверстия в сосуде (рис. 6.16), уносит с собой за время ∆t импульс ( − плотность жидкости, — площадь отверстия, − скорость истечения струи). Этот импульс сообщается вытекающей жидкости сосудом.

Рис. 6.16. Сосуд поставили на тележку,

под действием силы реакции тележка двигается

в направлении противоположном направлению струи

По третьему закону Ньютона сосуд получает от вытекающей жидкости за время ∆t импульс, т.е. испытывает действие силы реакции.

Если сосуд поставить на тележку, то под действием силы он придет в движение в направлении, противоположном направлению струи.

Найдем величину силы , воспользовавшись выражением для скорости истечения жидкости из отверстия – формула Торричелли (6.15):

. (6.18)

Если бы, как это может показаться на первый взгляд, сила совпадала по величине с силой гидростатического давления, которое жидкость оказывала бы на пробку, закрывающую отверстие, то была бы равна .

На самом деле сила оказывается в два раза большей. Это объясняется тем, что возникающее при вытекании струи движение жидкости в сосуде приводит к перераспределению давления, причем давление вблизи стенки, лежащей против отверстия, оказывается несколько большим, чем вблизи стенки, в которой сделано отверстие.

На реакции вытекающей струи газа основано действие реактивных двигателей и ракет. Реактивное движение, не нуждаясь для своего осуществления в наличии атмосферы, используется для полетов в космическое пространство.

Основоположником теории межпланетных сообщений является выдающийся русский ученый и изобретатель К.Э. Циолковский (1857—1935). Он дал теорию полета ракеты и обосновал возможность применения реактивных аппаратов для межпланетных сообщений. В частности, Циолковским была разработана теория движения составных ракет, в которых каждая последующая ступень вступает в действие после того, как предыдущая ступень, израсходовав полностью топливо, отделится от ракеты. Идеи Циолковского получили дальнейшее развитие и были осуществлены советскими учеными и инженерами, обеспечившими ведущую роль России в освоении и изучении космического пространства.