
- •Механика
- •Механика
- •Оглавление
- •Предисловие
- •Введение
- •Глава 1. Кинематика
- •Механическое движение
- •1.2. Некоторые сведения о векторах
- •1.3. Скорость
- •1.4. Ускорение
- •1.5. Угловая скорость и угловое ускорение
- •Глава 2. Динамика материальной точки
- •2.1. Первый закон Ньютона. Инерциальные системы отсчета
- •2.2. Второй закон Ньютона
- •2.3. Третий закон Ньютона
- •2.4. Сила. Силы трения
- •2.5. Импульс. Закон сохранения импульса
- •2.6. Центр масс. Движение тела переменной массы
- •Глава 3. Работа и энергия
- •3.1. Понятие о работе и энергии. Мощность. Консервативные
- •Кинетическая энергия
- •Потенциальная энергия
- •Закон сохранения механической энергии
- •Графическое представление энергии.
- •3.6. Применение законов сохранения энергии и импульса
- •Используя (3.32), получаем
- •Движение в центральном поле сил
- •Глава 4. Механика твердого тела
- •4.1. Движение твердого тела
- •4.2. Момент силы
- •4.3. Центр масс твердого тела и его движение
- •4.4. Момент импульса и закон его сохранения
- •4.5. Основное уравнение динамики вращательного движения
- •4.6. Момент инерции
- •4.7. Кинетическая энергия твердого тела
- •4.7.1. Вращение тела вокруг неподвижной оси
- •4.7.2. Работа внешних сил при вращении твердого тела
- •4.7.3. Кинетическая энергия тела при плоском движении
- •Глава 5. Тяготение. Неинерциальные системы
- •5.1. Развитие представлений о природе тяготения
- •5.2. Законы Кеплера. Закон всемирного тяготения
- •5.3. Гравитационное поле и его характеристики
- •5.4. Сила тяжести и вес. Невесомость
- •5.5. Космические скорости
- •5.6. Неинерциальные системы отсчета. Силы инерции
- •5.6.1. Силы инерции при ускоренном поступательном
- •5.6.2. Центробежная сила инерции
- •5.6.3. Сила Кориолиса
- •Глава 6. Элементы механики сплошных сред
- •6.1. Гидроаэростатика
- •6.1.1. Давление
- •6.1.2. Распределение давления в покоящихся жидкости и газе
- •6.1.3. Выталкивающая сила
- •6.2. Гидроаэродинамика
- •6.2.1. Линии и трубки тока. Неразрывность струи
- •6.2.2. Уравнение Бернулли
- •6.2.3. Измерение давления в текущей жидкости
- •6.2.4. Применение к движению жидкости закона сохранения
- •6.2.5. Силы внутреннего трения
- •6.2.6. Ламинарное и турбулентное течение
- •6.2.7. Движение тел в жидкостях и газах
- •6.2.8. Подъемная сила
- •Глава 7. Элементы специальной теории
- •7.1. Принцип относительности Галилея.
- •7.2. Постулаты специальной теории относительности
- •7.3. Преобразования Лоренца
- •7.4. Следствия из преобразований Лоренца
- •7.4.1. Одновременность событий в разных системах отсчета
- •7.4.2. Длительность событий в разных системах отсчета
- •7.4.3. Длина тел в разных системах отсчета
- •7.4.4. Релятивистский закон сложения скоростей
- •7.5. Интервал между событиями
- •7.6. Релятивистская динамика. Релятивистский импульс
- •7.7. Закон взаимосвязи массы и энергии
- •7.7.1. Кинетическая энергия релятивистской частицы
- •7.7.2. Закон взаимосвязи массы и энергии
- •7.7.3. Связь между энергией и импульсом частицы
- •Глава 8. Свободные гармонические колебания
- •8.1. Гармонические колебания и их характеристика
- •8.2. Механические гармонические колебания
- •8.3. Гармонический осциллятор. Пружинный, математический
- •8.4. Графическое изображение гармонических колебаний.
- •8.5. Сложение колебаний одинакового направления
- •8.6. Сложение взаимно перпендикулярных колебаний
- •Глава 9. Свободные Затухающие колебания
- •9.1. Дифференциальное уравнение свободных затухающих
- •9.2. Основные характеристики затухающих колебаний
- •Глава 10. Вынужденные колебания
- •10.1. Дифференциальное уравнение вынужденных колебаний
- •10.2. Решение дифференциального уравнения вынужденных
- •10.3. Резонанс. Примеры резонансных явлений
- •Глава 11. Волны в упругой среде
- •11.1. Упругие волны
- •11.2. Уравнение плоской и сферической волн
- •11.3. Уравнение плоской волны, распространяющейся
- •11.4. Волновое уравнение
- •11.5. Скорость распространения упругих волн
- •11.6. Энергия упругой волны
- •11.6.1. Плотность энергии упругой волны
- •11.6.2. Плотность потока энергии
- •11.7. Стоячие волны
- •11.7.1. Уравнение стоячей волны
- •11.7.2. Энергия стоячей волны
- •11.8. Эффект Доплера для звуковых волн
- •Литература
- •Механика
- •302020, Г. Орел, Наугорское шоссе, 29.
5.6.2. Центробежная сила инерции
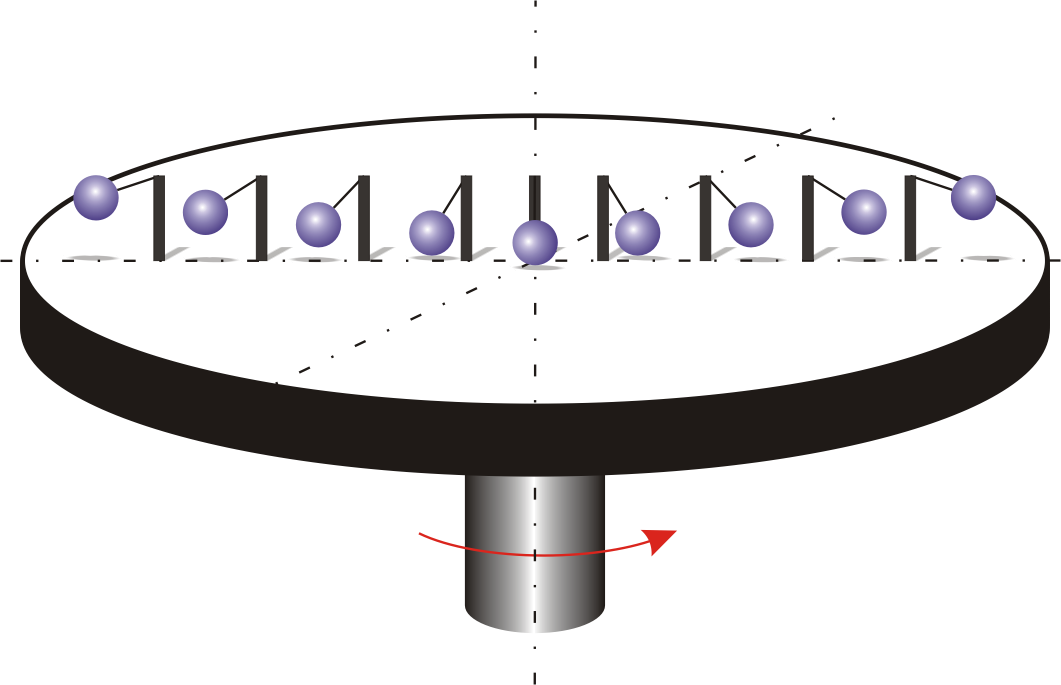
Пусть диск равномерно вращается с угловой скоростью (-const) вокруг вертикальной оси, проходящей через его центр. На диске, на разных расстояниях от оси вращения на столбиках подвешены шарики массой m (рис. 5.6а). При вращении этой системы шарики отклоняются от вертикали на некоторый угол .

а б
Рис. 5.6. Положение шариков на вращающемся диске
а - положение шариков, помещенных на различных расстояниях от оси вращения,
б – силы, действующие на отдельный шарик
В
инерциальной системе отсчёта, связанной,
например с помещением, где установлен
диск, шарик равномерно вращается по
окружности радиусом R
(R
- расстояние
от центра вращающегося шарика до оси
вращения.) Следовательно, на него
действует сила, равная
![]() и направленная перпендикулярно оси
вращения диска. Она является равнодействующей
силы тяжести
и направленная перпендикулярно оси
вращения диска. Она является равнодействующей
силы тяжести
![]() и силы натяжения нити
и силы натяжения нити
![]() :
:
![]() .
Когда движение шарика установится, то
.
Когда движение шарика установится, то
![]() (рис. 5.6б), откуда
(рис. 5.6б), откуда
![]()
![]()
![]() ,
,
т.е. углы отклонения нитей маятников будут тем больше, чем больше расстояние R от центра шарика до оси вращения диска и чем больше угловая скорость вращения .
Относительность
системы отсчёта, связанной с вращающимся
диском, шарик покоится, что возможно,
если сила
![]() уравновешивается равной и противоположно
направленной ей силой
уравновешивается равной и противоположно
направленной ей силой
![]() ,
которая является ничем иным, как силой
инерции, так как на шарик никакие другие
силы не действуют. Сила
,
которая является ничем иным, как силой
инерции, так как на шарик никакие другие
силы не действуют. Сила
![]() ,
называемая центробежной
силой инерции,
направлена по горизонтали от оси вращения
диска и равна
,
называемая центробежной
силой инерции,
направлена по горизонтали от оси вращения
диска и равна
![]() .
(5.12)
.
(5.12)
Действия центробежных сил инерции подвергаются, например, пассажиры в движущемся транспорте на поворотах, летчики при выполнении фигур высшего пилотажа, центробежные силы используются во всех центробежных механизмах: насосах, сепараторах и т.д., где они достигают огромных значений. При проектировании быстро вращающихся деталей машин (роторов, винтов самолетов и т.д.) принимаются специальные меры для уравновешивания центробежных сил инерции.
Из формулы (5.12) следует, что центробежная сила инерции действует во вращающихся системах на все тела, удаленные от оси вращения на конечное расстояние, независимо от того, покоятся ли они в этой системе или движутся относительно нее.
5.6.3. Сила Кориолиса
На тело, движущееся во вращающейся системе отсчета также действует сила инерции, которую называют силой Кориолиса по имени открывшего ее французского физика и инженера Гюстава Гаспара Кориолиса (1792 – 1843).
Пусть шарик массой m движется с постоянной скоростью v вдоль радиуса равномерно вращающегося диска (v – const, – const, v). Если диск не вращается, то шарик, направленный вдоль радиуса, движется по радиальной прямой и попадает в точку А (рис. 5.7), если же диск привести во вращение в направлении, указанном стрелкой, то шарик катится по кривой ОВ, причем его скорость относительно диска изменяет свое направление. Это возможно лишь тогда, если на шарик действует сила, перпендикулярная скорости v.
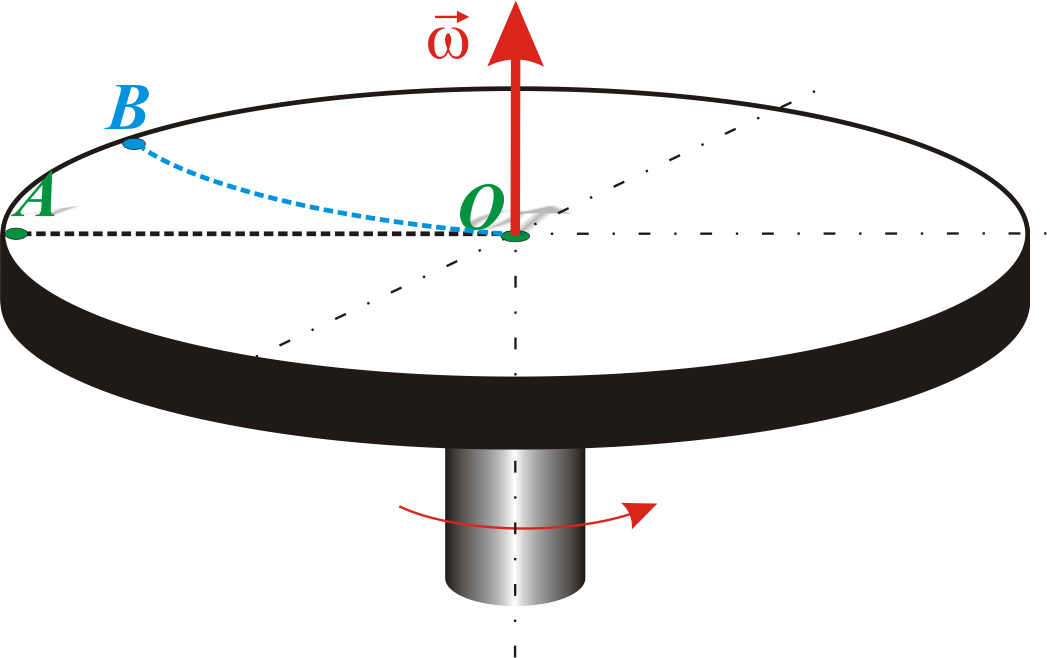
Рис. 5.7. Движение шарика на вращающемся диске
Для того, чтобы заставить шарик катиться по вращающемуся диску вдоль радиуса, используем жестко укрепленный вдоль радиуса диска стержень, на котором шарик катится без трения равномерно и прямолинейно со скоростью v (рис. 5.8). При отклонении шарика стержень действует на него с некоторой силой F. Теперь относительно диска шарик движется равномерно и прямолинейно, что можно объяснить тем, сила F уравновешивается приложенной к шарику силой инерции FК, перпендикулярной скорости v.
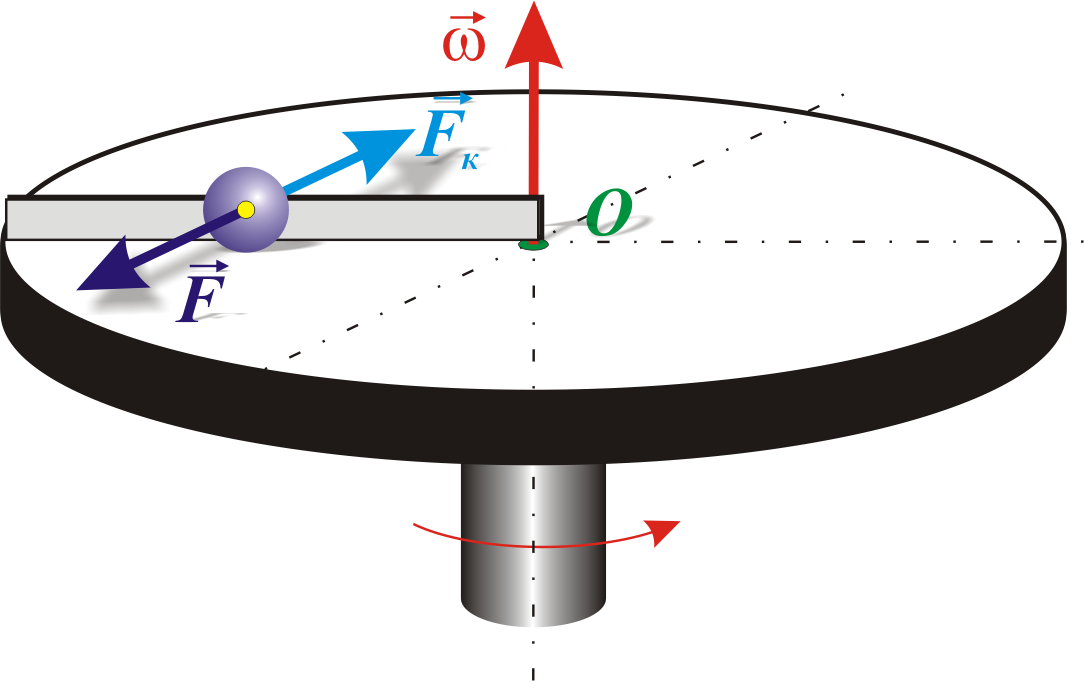
Рис. 5.8. Силы, действующие на шарик,
движущийся на вращающемся диске
Эта сила и называется силой Кориолиса:
![]() .
(5.13)
.
(5.13)
Вектор
![]() перпендикулярен векторам скорости тела
перпендикулярен векторам скорости тела
![]() и угловой скорости вращения системы
отсчета
и угловой скорости вращения системы
отсчета
![]() в соответствии с правилом правого винта.
в соответствии с правилом правого винта.
Действием этой силы объясняется ряд наблюдаемых на Земле явлений. Например, тело, свободно падая с вершины башни, движется не по вертикали, а слегка отклоняется к востоку. Это отклонение тем больше, чем больше высота башни, и зависит от географической широты места проведения опыта. При прочих равных условиях величина смещения максимальна на экваторе и равна нулю на полюсах. Рассмотрим случай падения на экваторе с точки зрения неподвижного и подвижного наблюдателей.
Для неподвижного наблюдателя (как бы смотрящего со стороны на Землю вместе с башней) на свободно падающее тело действует только сила тяготения к Земле F. Эта сила сообщает телу ускорение, направленное к центру Земли. Следовательно, сила F не изменяет численного значения линейной скорости тела в суточном сращении земли. Иными словами, в процессе падения тело сохраняет значение скорости, соответствующее вершине башни v1 (рис. 5.9). Линейная же скорость основания башни v меньше, чем скорость верхушки башни v1:
![]() ,
,
где R – радиус Земли,
– угловая скорость ее суточного вращения.
Поэтому точка приземления тела должна быть несколько смещена к востоку (в направлении вращения Земли) по сравнению с вершиной башни.

Рис. 5.9. Смещение падающего с высоты h
тела в направлении вращения Земли
Для подвижного наблюдателя на тело, помимо силы F тяготения к Земле, действует центробежная Fц и кориолисова FK cилы инерции (рис. 5.10). Первые две силы направлены радиально: F - к центру Земли, Fц - от центра Земли. Поэтому их равнодействующая должна была бы вызвать строго вертикальное падение тела. Однако кориолисова сила инерции FK перпендикулярна к скорости v падения тела, поэтому вызывает искривление его траектории и смещение точки приземления к востоку.

Рис. 5.10. Силы, действующие на тело падающее с высоты h
во вращающейся системе отсчета
Аналогичным образом можно объяснить, почему реки, текущие в меридиональном направлении, всегда подмывают вполне определенный берег: правый по течению – для рек северного полушария Земли и левый – для рек южного полушария. Например, реки северного полушария, текущие с севера на юг, подмывают западный берег.
С точки зрения неподвижного наблюдателя численные значения линейных скоростей точек поверхности Земли в ее суточном вращении зависят от географической широты :
![]() ,
,
где v0 – линейная скорость точек экватора. Поэтому частицы воды, перемещаясь с севера на юг, должны увеличивать свою линейную скорость v. Так как эта скорость направлена с запада на восток, то ее увеличение может осуществляться только за счет взаимодействия частиц воды с западным берегом реки, который при этом подмыва-ется.
Для подвижного наблюдателя на частицы воды, движущиеся с севера на юг с относительной скоростью v, действуют кориолисовы силы инерции FK, которые направлены с востока на запад (рис. 5.11). Поэтому частицы воды отклоняются в том же направлении, подмывая западный берег реки.

Рис. 5.11. Направление силы Кориолиса для частиц воды (для рек)
текущих с севера на юг
Неинерциальность земной системы отсчета легко обнаружить на опыте с помощью маятника Фуко. Фуко обнаружил, что плоскость качаний маятника постепенно изменяет свою ориентацию по отношению к земной системе отсчета, это в свое время явилось одним из доказательств вращения Земли. Если бы не было силы Кориолиса, то плоскость колебаний качающегося маятника оставалась бы неизменной. Действие же сил Кориолиса приводит к вращению плоскости колебания вокруг вертикального направления.
Для любого из тел, находящихся в неинерциальной системе отсчета, силы инерции являются внешними, следовательно, здесь нет замкнутых систем. Это означает, что в неинерциальных системах отсчета не выполняются законы сохранения импульса, энергии и момента импульса.
Силы инерции, так же как и силы тяготения пропорциональны массам тел. При некоторых условиях силы инерции и силы тяготения невозможно различить. Например, движение тел в равноускоренном лифте происходит точно так же, как и в неподвижном лифте, висящем в однородном поле тяжести. Никакой эксперимент, выполненный внутри лифта, не может отделить однородное поле тяготения от однородного поля сил инерции. Аналогия между силами тяготения и силами инерции лежит в основе принципа эквивалентности гравитационных сил и сил инерции (принципа эквивалентности Эйнштейна). Все физические явления в поле тяготения происходят совершенно так же, как и в соответствующем поле сил инерции, если напряженность обоих полей в соответствующих точках пространства совпадают, а прочие начальные условия для рассматриваемых тел одинаковы. Этот принцип является основой общей теории относительности.
