Глава 1. Кинематика

1. Механическое движение

Реальный мир, начиная от элементарных частиц и различных полей, от атомов и молекул и кончая такими объектами Вселенной, как звезды и галактики, представляет собой единую материальную систему. Будем обозначать словом материя все то, из чего состоят тела природы, а также разного рода поля, например, гравитационное. Материя (материальная система) находится в состоянии непрерывного движения. Формы движения многочисленны и разнообразны. Наиболее простой из всех форм является механическое движение. Механическое движение – это изменение с течением времени взаимного расположения тел и их частей, оно представляет собой перемещение в пространстве со временем одних материальных тел относительно других. Представление о пространстве и времени являются основными понятиями в физике. Фундаментальность этих понятий заключается в том, что их невозможно выразить, объяснить через какие- либо более простые понятия. Для изучения законов природы нужны не формальные их определения, а их свойства, познаваемые на опытах. Опыт говорит о том, что физическое пространство трехмерно, однородно и изотропно, а время одномерно и однородно.

Трехмерность физического пространства проявляется в том, что для указания места, где происходят какие-либо события, достаточно трех пространственных координат, трех чисел.

Однородность физического пространства проявляется в независимости физических законов от их места проявления. Опыт, поставленный в одинаковых физических условиях в разных местах, дает одинаковые результаты.

Изотропность физического пространства проявляется в независимости физических законов от ориентации физической системы в пространстве.

Одномерность времени проявляется в том, что для указания момента наступления какого-либо события или длительности какого-либо процесса достаточно одного числа.

Однородность времени проявляется в неизменности физических законов: опыт, поставленный в одинаковых условиях в разные моменты времени дает одинаковые результаты.

Пространство отражает взаимное положение протяженных объектов, а время - продолжительность следующих друг за другом материальных процессов. Следовательно, пространство и время зависят от движущейся материи и от происходящих в ней физических процессов.

Однородность времени, однородность и изотропность пространства отражают симметрию физического мира. Значительное количество законов физики объясняются свойствами симметрии пространства и времени, например, законы сохранения энергии, импульса, момента импульса.

Раздел физики, занимающийся изучением закономерностей механического движения и взаимодействия тел, называется механикой. Механику тел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме) называют классической механикой. Основы ее были разработаны И. Ньютоном (1643-1727) и ее обычно называют ньютоновской механикой. Законы движения макроскопических тел со скоростями сравнимыми со скоростью света изучаются релятивистской механикой, основанной на специальной теории относительности, сформулированной А. Эйнштейном (1879-1955). Для описания движения микроскопических тел (атомы, элементарные частицы) законы классической механики неприменимы - они заменяются законами квантовой механики.

В классической механике принимаются следующие постулаты, характеризующие непрерывность и однородность пространства и времени.

Постулат 1. Возможно одновременное измерение с любой точностью любых физических величин, характеризующих движение макроскопических тел. Процесс измерения не изменяет состояние движения макроскопического тела, не изменяет самой измеряемой величины. Например, измерение положения тела в пространстве не сказывается на его координатах, измерение продолжительности какого-либо механического процесса не влияет на его длительность.

Постулат 2. Продолжительность любого процесса одинаково во всех системах отсчета, движущихся относительно друг друга произвольным образом, т.е.

∆t = ∆t^',

где ∆t и ∆t^' – продолжительность одного и того же процесса в двух различных системах отсчета.

Этим постулатом утверждается абсолютность временных интервалов между событиями.

Постулат 3. Расстояние между любыми точками пространства в данный момент времени одинаково во всех системах отсчета, т.е.

∆l = ∆l ^',

где ∆l и ∆l ^' – расстояние между одними и теми же точками пространства в двух различных системах отсчета.

Механика делится на три раздела: кинематику, динамику, статику.

Кинематика изучает движение тел, не рассматривая причины, которые это движение обуславливают.

Динамика изучает законы движения тел и причины, которые вызывают или изменяют это движение.

Статика изучает законы равновесия системы тел. Если известны законы движения тел, то из них можно установить и законы равновесия. Поэтому законы статики отдельно от законов динамики физики не рассматривают.

Все окружающие нас тела состоят из огромного числа атомов или молекул, т.е. представляют собой макроскопические системы.

Решая ту или иную конкретную задачу механики, всегда приходится мысленно выделить из множества тел только те, которые играют в данной задаче существенную роль. Такая мысленно выделенная совокупность рассматриваемых тел называется механической системой. В зависимости от условий такой задачи в механике пользуются различными упрощенными физическими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело и др. Выбор той или иной модели нужно производить так, чтобы учесть все существенные особенности поведения реального тела в данной задаче и отбросить все второстепенные, усложняющие решение этой задачи.

Материальной точкой называют тело, формы и размеры которого несущественны в данной задаче.

Системой материальных точек называют совокупность тел, каждое из которых можно рассматривать как материальную точку. Материальная система может быть как дискретной, состоящей из отдельных материальных точек, так и сплошной, представляющее непрерывное распределение вещества. В качестве примера дискретной совокупности можно назвать Солнечную систему, разреженный газ, а сплошной среды - твердые, жидкие и газообразные тела.

Абсолютно твердым телом называют тело, расстояние между любыми двумя точками которого всегда остается неизменным.

Всякое движение твердого тела можно представить как комбинацию поступательного и вращательного движений. Поступательное движение - это такое движение, при котором любая прямая, связанная с движением тела, остается параллельной самой себе. Вращательное движение - это движение, при котором все точки тела движутся по окружностям, с центрами лежащими на одной и той же прямой, называемой осью вращения.

Абсолютно упругим называют тело, если его деформации подчиняются закону Гука, т.е. пропорциональны вызывающим их силам. После прекращения внешнего механического действия на такое тело оно полностью восстанавливает свои первоначальные размеры.

Абсолютно неупругим телом называют тело, которое после прекращения внешнего воздействия полностью сохраняет деформированное состояние, вызванное этим действием.

Для однозначного определения положения тела в произвольный момент времени необходимо выбрать систему отсчета. Системой отсчета называется система координат, снабженная часами и жестко связанная с абсолютно твердым телом, по отношению к которому определяется положение других тел в различные моменты времени. При этом под часами подразумевается любое устройство, используемое для измерения времени или, точнее, промежутка времени между событиями, т.к. в силу однородности времени, начало их отсчета можно выбирать произвольно. В дальнейшем будем называть земной или лабораторной систему отсчета, жестко связанную с Землей. В декартовой системе координат, используемой наиболее часто, положение точки в данный момент времени характеризуется тремя координатами x, y, z или радиус-вектором , проведенным из начала системы координат в данную точку (рис. 1.1).

Рис. 1.1. Положение точки A в декартовой

системе координат характеризуется тремя

координатами или радиус-вектором

При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется скалярными уравнениями

, (1.1)

которые эквивалентны векторному уравнению

. (1.2)

Уравнения (1.1) и (1.2) называются кинематическими уравнениями движения материальной точки. Например: кинематические уравнения имеют вид:

1. Для равномерного движения вдоль оси ставится “+”, когда скорость и ось сонаправлены и “–”, когда скорость и ось противоположны.

2. Для равнопеременного движения уравнение координаты имеет вид: .

Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы. Если материальная точка свободно движется в пространстве, то она обладает тремя степенями свободы (x, y, z). Если она движется по некоторой плоской поверхности, то двумя степенями свободы, если вдоль некоторой прямой линии, то одной степенью свободы.

Исключая t в уравнениях (1.1), (1.2), получим уравнение траектории движения материальной точки. Траектория движения материальной точки - это линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.

Рассмотрим движение материальной точки вдоль произвольной траектории AB (рис. 1.2). - длина пути - длина участка траектории материальной точки, пройденная с момента начала отсчета времени, скалярная функция времени =. Вектор называется перемещением - вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса - вектора точки за рассматриваемый промежуток времени).

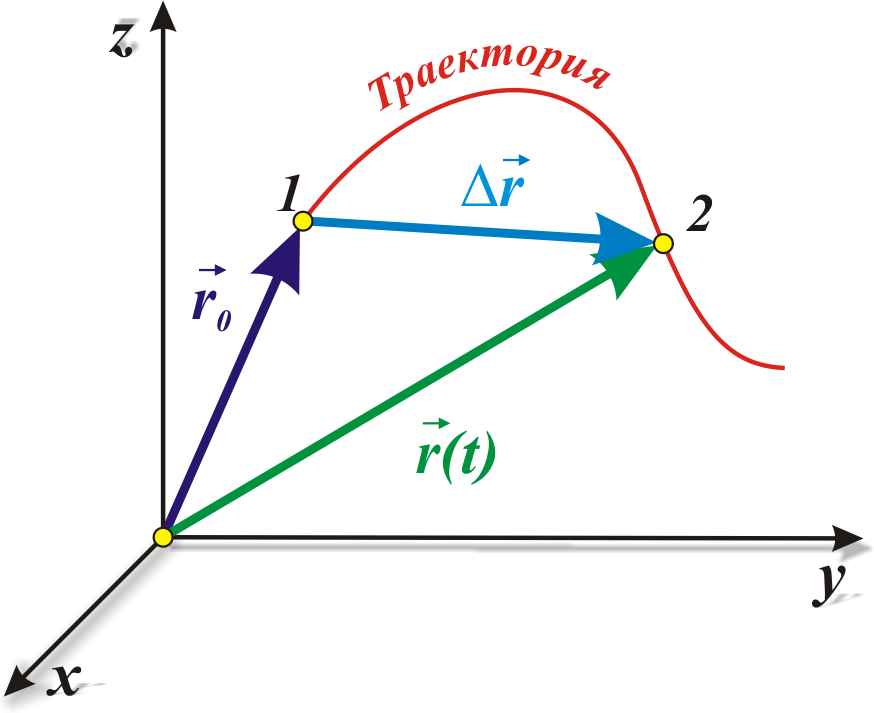
Рис. 1.2. Движение материальной точки

по криволинейной траектории:

∆s – длина пути, – перемещение

Предположим, что частица совершает последовательно два перемещения: и (рис. 1.3). Суммой этих перемещений естественно назвать такое перемещение , которое приводит к тому же результату, что и первые два перемещения вместе.

Рис. 1.3. Два последовательных перемещения

материальной точки, вектор геометрическая

сумма этих перемещений

Таким образом, перемещения характеризуются числовым значением и направлением и, кроме того, складываются по правилу параллелограмма, т.е. перемещение есть вектор.

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль вектора перемещения | | равен пройденному пути ∆s, т.е. | |=∆s.