5.6. Неинерциальные системы отсчета. Силы инерции

До сих пор для описания движения материальной точки или тела, т.е. системы материальных точек, мы всегда пользовались инерциальными системами отсчета. В то же время во многих случаях необходимо изучать движение материальной точки или тела по отношению к неинерциальной системе отсчета. Так, например, движение тел на Земле естественно рассматривать в скрепленной с ней земной системе отсчета, которая, строго говоря, не является инерциальной. В первом приближении можно обычно пренебречь неинерциальностью этой системы отсчета, однако возможность такого допущения требует специального обоснования, так как иначе неясна величина допускаемых при этом погрешностей. Целый ряд явлений – "самопроизвольный" поворот плоскости качаний маятника (опыт Фуко), отклонение свободно падающих тел к востоку, подмывание одного из берегов реками, текущими в меридиональном направлении, и т.д. – вообще не могут быть объяснены в случае пренебрежения неинерциальностью земной системы отсчета.

Системы отсчета, движущиеся относительно инерциальной системы с ускорением, называются неинерциальными. В неинерциальных системах законы Ньютона, вообще говоря, уже несправедливы. Однако законы динамики можно применять и для них, если кроме сил, обусловленных воздействием тел друг на друга, ввести в рассмотрение силы особого рода – так называемые силы инерции.

Если учесть силы инерции, то второй закон Ньютона будет справедлив для любой системы отсчета: произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (включая и силы инерции). Силы инерции при этом должны быть такими, чтобы вместе с силами , обусловленными воздействием тел друг на друга, они сообщали телу ускорение , каким оно обладает в неинерциальных системах отсчета, т.е.

.

Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, поэтому нужно учитывать следующие случаи проявления этих сил: 1) силы инерции при ускоренном поступательном движении системы отсчета; 2) силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета; 3) силы инерции, действующие на тело, движущееся во вращающейся системе отсчета.

Силы инерции реально действуют на материальную точку в неинерциальной системе отсчета и могут быть измерены, например, с помощью пружинного динамометра. Однако в отличие от "обычных" сил для сил инерции нельзя указать, действие каких именно тел на рассматриваемую материальную точку они выражают. Следовательно, к этим силам неприменим третий закон Ньютона. Поэтому силы инерции иногда называют "фиктивными", однако с их помощью могут быть объяснены многие явления.

5.6.1. Силы инерции при ускоренном поступательном

движении системы отсчета

Если тележку с подвешенным на кронштейне шариком массой m (рис. 5.5) привести в поступательное движение с ускорением , то нить начнет отклоняться от вертикали назад, до такого угла , пока результирующая сила не обеспечит ускорение шарика, равное . Таким образом, результирующая сила направлена в сторону ускорения тележки и для установившегося движения шарика (шарик теперь движется вместе с тележкой с ускорением ) равна

, откуда ,

т.е. угол отклонения от вертикали тем больше, чем больше ускорение тележки.

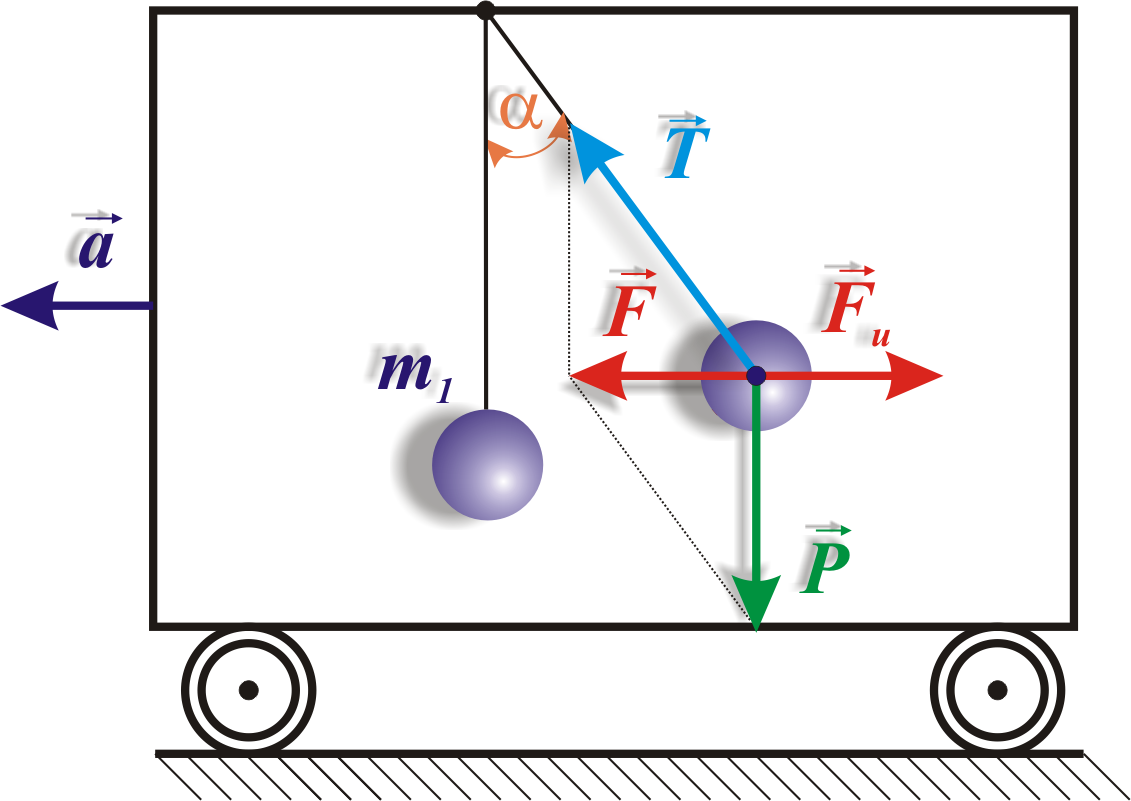
Рис. 5.5. Силы инерции при ускоренном поступательном

движении системы отсчета

Относительно системы отсчета, связанной с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила уравновешивается равной и противоположно направленной ей силой , которая является ничем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Таким образом,

.

Проявление сил инерции при поступательном движении наблюдается в повседневных явлениях. В справедливости сказанного каждый не раз убеждался, пользуясь любым из видов транспорта. Так, например, люди, неподвижно стоящие в равномерно и прямолинейно движущемся трамвае, отклоняются назад при ускорении движения трамвая или вперед – при его замедлении. Если бы пол трамвая был идеально гладким, то при всяком изменении скорости трамвая его пассажиры должны были бы скользить по полу, несмотря на то, что на них не действуют никакие горизонтальные силы.