2. Графическое представление энергии.

Условия равновесия механических систем

График зависимости потенциальной энергии от некоторого аргумента называется потенциальной кривой. Анализ потенциальных кривых позволяет определить характер движения тела.

Рассмотрим консервативные системы, т.е. системы, в которых взаимные превращения механической энергии в другие виды отсутствуют. Представим графически потенциальную энергию тела в однородном поле тяжести и энергию упругодеформированного тела.

Потенциальная энергия тела массой m, поднятого на высоту h над поверхностью Земли П(h)=mgh. График данной зависимости П=П(h) – прямая линия, проходящая через начало координат (рис. 3.2), угол наклона которой к оси h тем больше, чем больше масса тела (так как tg=mg).

Пусть полная энергия тела равна Е (ее график – прямая, параллельная оси h). На высоте h₁ (отмеченной на оси h) тело обладает потенциальной энергией П, которая определяется отрезком вертикали (на рис. 3.2 отрезок П показан вертикальной стрелкой), тогда кинетическая энергия Т задается отрезком, заключенным между прямой Е и графиком П(h). Из графика следует, что если h=h_max, то Т=0 и П=Е=mgh_max, т.е. потенциальная энергия становится максимальной и равной полной энергии.

Рис. 3.2. Графическое представление потенциальной энергии

для тела в однородном поле тяжести

По графику на рис. 3.2 можно найти скорость тела на высоте h:

Т=Е–П, т.е. ,

откуда

.

Зависимость потенциальной энергии упругой деформации П= от деформации х (х – смещение пружины от положения равновесия х₀) имеет вид параболы (рис. 3.3), где график заданной полной энергии тела Е – прямая, а значения Т и П (показаны вертикальными стрелками) определяются так же, как на рис. 3.2. Из рис. 3.3 следует, что с возрастанием деформации х потенциальная энергия тела возрастает, а кинетическая – уменьшается. Кинетическая энергия в свою очередь может возрастать только за счет уменьшения потенциальной энергии. Абсцисса х_max определяет максимально возможную деформацию растяжения пружины, а – х_max – максимально возможную деформацию сжатия пружины. При х= х_max потенциальная энергия становится максимальной и равной полной энергии. Пружина (тело) не может сместиться левее –х_max или правее х_max, в этом случае говорят, что тело находится в потенциальной яме с координатами –х_max  х  х_max.

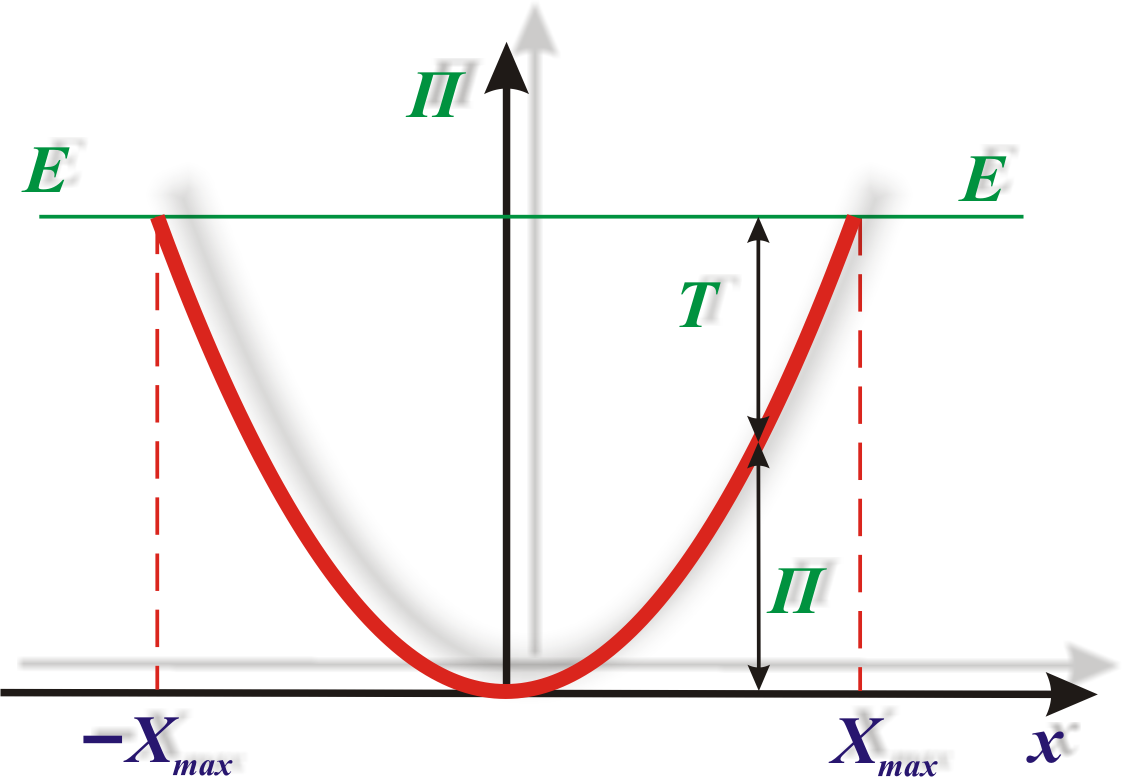
Рис. 3.3. Графическое представление потенциальной энергии

для упругодеформированного тела

В общем случае потенциальная кривая может иметь довольно сложный вид, например с несколькими чередующимися максимумами и минимумами (рис. 3.4). Проанализируем эту потенциальную кривую.

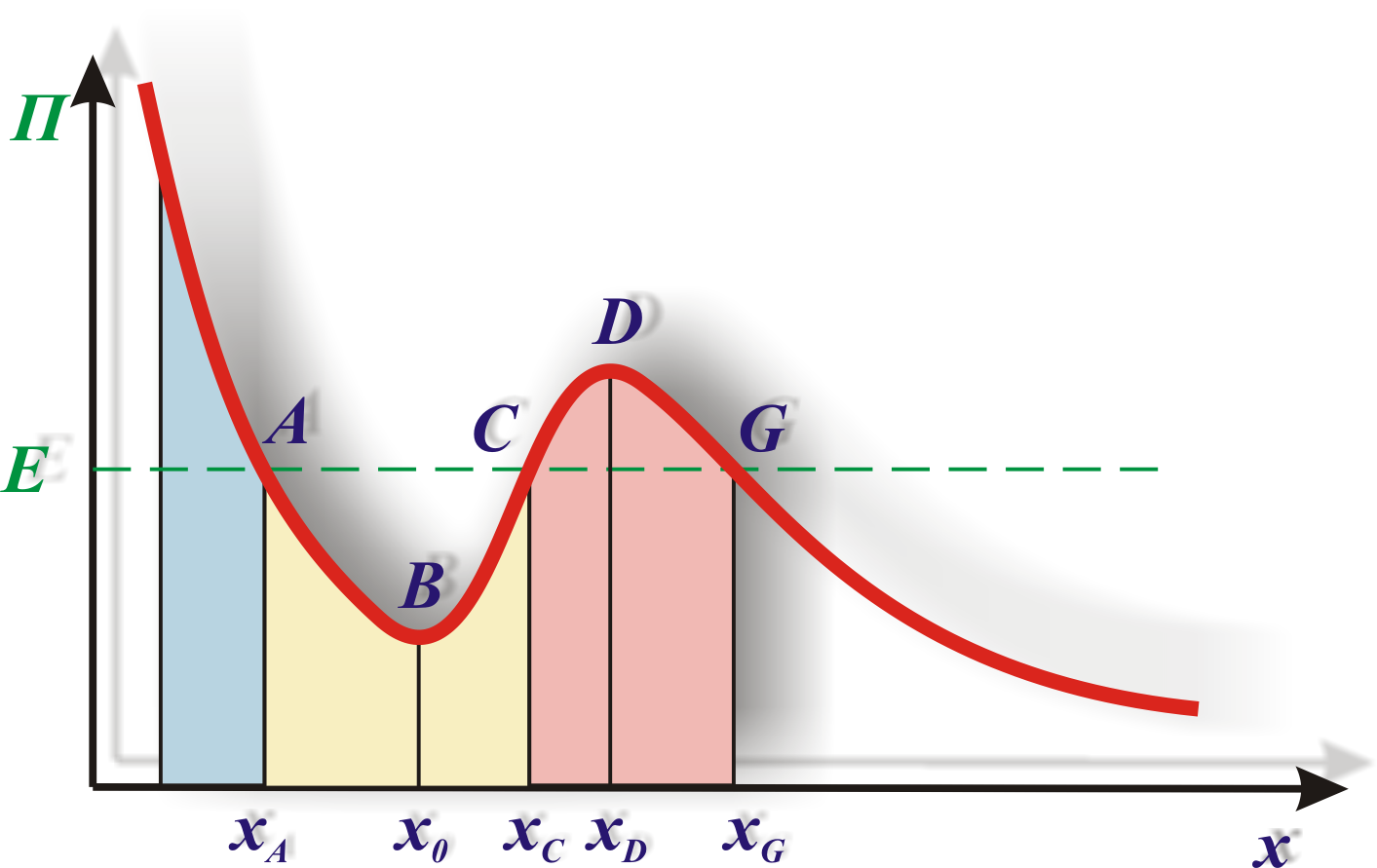
Рис. 3.4. Потенциальная кривая (общий случай)

Если Е – заданная полная энергия частицы, то частица может находиться только там, где П(х)  Е, т.е. в незаштрихованных областях. Переходить из одной области в другую частица не может, т.к. ей препятствует потенциальный барьер CDG, с шириной равной интервалу значений х, при которых Е<П, а его высота определяется разностью П_max – Е. Для того, чтобы частица смогла преодолеть потенциальный барьер, ей необходимо сообщить дополнительную энергию, равную высоте барьера или превышающую её. Таким образом, потенциальный барьер – это область через которую частица не может проникнуть имея данный запас полной энергии. В области АВС частица оказывается запертой в потенциальной яме и совершает колебания между точками х_А и х_С. Потенциальная яма – область, в которой частица может совершать колебания, но не может покинуть эту область.

В точке В с координатой х₀ потенциальная энергия частицы минимальна. Условие минимума потенциальной энергии имеет вид:

. (3.22)

При смещении частицы из положения х₀ влево или вправо она испытывает действие возвращающей силы, которая стремится вернуть частицу в положение равновесия, поэтому положение х₀ является положением устойчивого равновесия. Условие (3.22) выполняется также для х равного х_D, однако это равновесие будет неустойчивым: достаточно слегка вывести частицу из этого положения, как возникает сила, которая будет удалять её от положения х_D.

Если частица при своем движении не может удалиться в бесконечность, движение называется финитным. Если же частица может уходить сколь угодно далеко, движение называют инфинитным. Частица в потенциальной яме совершает финитное движение.