Предел функции в бесконечности и точке Предел функции в бесконечности

С понятием предела числовой последовательности тесно связано понятие предела функции в бесконечности. Если в первом случае переменная , возрастая, принимает лишь целые значения, то во втором случае переменная , изменяясь, принимает любые значения.

Определение. Число называется пределом функции при , стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа , найдется такое положительное число (зависящее от ; ), что для всех , таких, что , верно неравенство

(1)

Этот предел функции обозначается или при .

С помощью логических символов определение предела запишется

.

Смысл определения остается тем же, что для предела числовой последовательности: при достаточно больших по модулю значениях значения функции как угодно мало отличаются от числа (по абсолютной величине).

Выясним геометрический смысл предела функции в бесконечности. Неравенство (1) равносильно двойному неравенству , соответствующему расположению части графика в полосе шириной (рис.1).

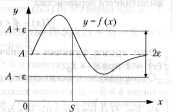
Рис.1

Итак, число есть предел функции при , если для любого найдется такое число , что для всех таких, что , соответствующие ординаты графика функции будут заключены в полосе , какой бы узкой она ни была.

Пример. Доказать, что .

Решение: Для любого неравенство (1) или выполняется при .Итак, для любого существует такое число , что для всех таких, что , будет верно неравенство , где , а это и означает, что .

Замечание: Приведенное определение предела при предполагает неограниченное возрастание независимой переменной по абсолютной величине. В то же время можно сформулировать понятие предела при стремлении к бесконечности определенного знака, т.е. при или . В первом случае неравенство (1) должно выполняться для всех , а во втором для всех .

Предел функции в точке

Пусть - любое действительное число (точка на числовой прямой). Окрестностью точки называется любой интервал , содержащий точку . В частности интервал , где , называется -окрестностью точки . Число называется центром , а число -радиусом (рис.2).

Рис.2

Пусть функция задана в некоторой окрестности точки , кроме, может быть, самой точки .

Определение. Число называется пределом функции при (или в точке ), если для любого, даже сколь угодно малого положительного числа , найдется такое положительное число (зависящее от , т.е. ), что для всех , не равных и удовлетворяющих условию

, (2)

выполняется неравенство

. (3)

Этот предел функции обозначается или при .

С помощью логических символов определение предела запишется

.

Смысл определения предела функции в точке состоит в том, что для всех значений , достаточно близких к , значения функции как угодно мало отличаются от числа (по абсолютной величине).

Рассмотрим геометрический смысл предела функции в точке. Неравенство равносильно двойному неравенству , соответствующему расположению части графика в полосе шириной (рис.3).

Рис.3

Аналогично неравенство равносильно двойному неравенству , соответствующему попаданию точек в -окрестность точки .

Число есть предел функции при , если для любого найдется такая -окрестность точки , что для всех из этой окрестности соответствующие ординаты графика функции будут заключены в полосе , какой бы узкой она ни была.

Пример 2. Доказать, что .

Решение: пусть . Тогда неравенство (3) будет выполняться при , , , ,

, .

Аналогично при то же неравенство (3) будет верно при .

Для любого неравенство (3) будет выполняться при .

Итак, при любом существует такое число , что для всех и удовлетворяющих условию верно неравенство , где , а это и означает, что .

Замечание 1. Определение предела не требует существования функции в самой точке , так как рассматривает значения в некоторой окрестности этой точки. Другими словами, рассматривая , предполагается, что стремится к , но не достигает значения . Поэтому наличие или отсутствие предела при определяется поведением функции в окрестности точки , но не связано со значением функции (или его отсутствием) в самой точке .

Замечание 2. Если при стремлении к переменная принимает лишь значения, меньшие , или, наоборот, лишь большие , и при этом функция стремится к некоторому числу , то говорят об односторонних пределах функции соответственно слева и справа . Очевидно, что определение этих пределов будет аналогично рассмотренному выше при , если вместо значений , удовлетворяющих условию (2), при которых верно неравенство (3), рассматривать значения , такие, что при (слева), или значения , такие, что при (справа).

Разумеется, если

, то .