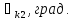Курсовая работа / Курсовая работа3
.docxФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
Кафедра теории электрических цепей
Курсовая работа «Анализ активного RC-фильтра»
Выполнил: студент группы ИКВТ-61, Козырев А.Б.,
« » 2018 г. ___________/А.Б. Козырев/
Принял: к.т.н., доцент Замулин О. Л.
« » 2018 г. ___________/О.Л. Замулин/
Вариант: Г
Параметр N: 4
Параметр M: 2
ФИО: Козырев Андрей Бушраевич
Номер зачётной книжки:
Факультет: ИКСС
Направление: 09.03.01
Группа: ИКВТ-61
ФИО преподавателя: Замулин Олег Леонидович
Оглавление
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ 1
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» 1
(СПбГУТ) 1
1.Расчётные формулы 4
2.Содержание задания 6
3.Комплексная передаточная функция 11
4.Переходная характеристика цепи 15
5.Спектральное представление 19
6.Разложение на гармоники 24
-
Расчётные формулы
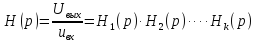
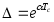
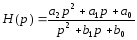
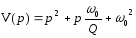
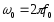

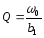
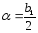
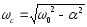
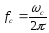
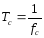
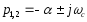
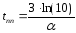
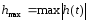
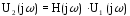
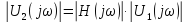
-
Содержание задания
Схема ARC-цепи №19.
схема 2.1.
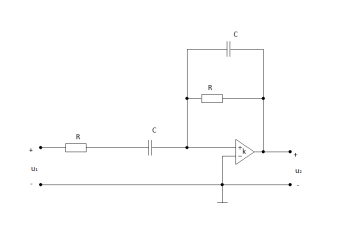
Значения параметров ARC-цепи
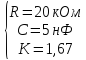
Пронумеруем узлы
схема 2.2.
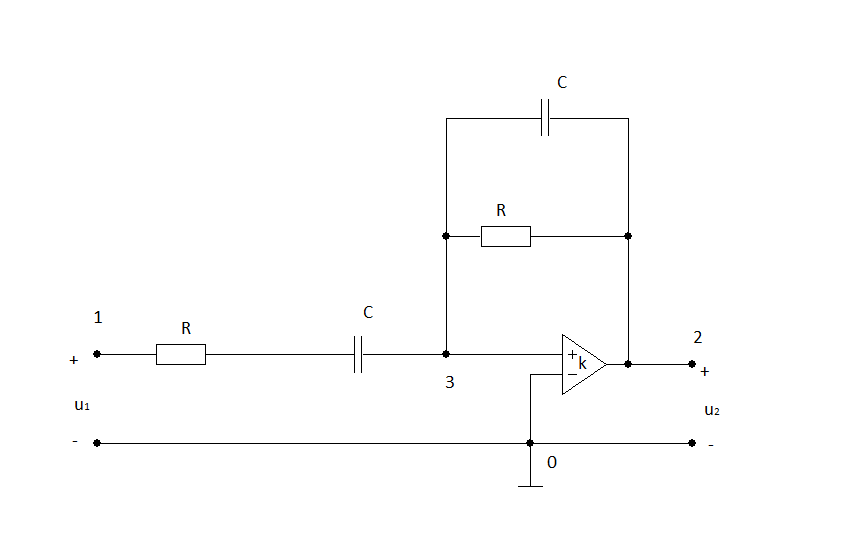
Рассмотрим операторную схему замещения
схема 2.3.
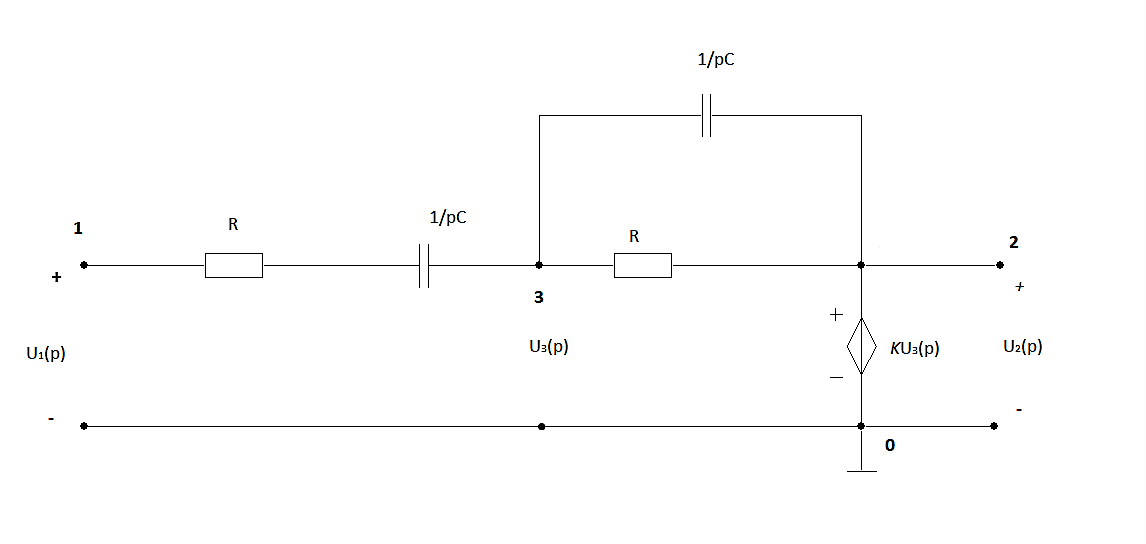
Найдём операторную передаточную функцию
Составим
и решим
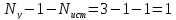 узловое уравнение
узловое уравнение
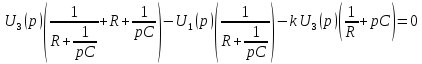
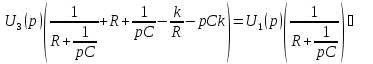
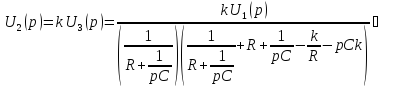
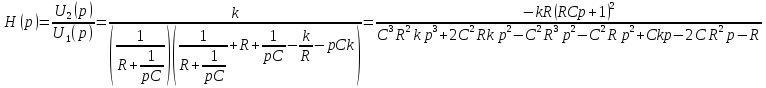
Представляя операторную передаточную функцию в общем виде:
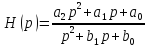
Получим
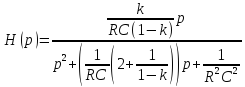
Знаменатель передаточной функции v(p) является полиномом Гурвица.
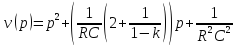
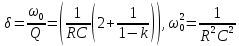
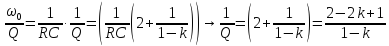
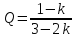
Найдём численные значения параметров:
Резонансная частота колебательного контура:
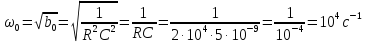
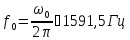
Добротность колебательного контура:
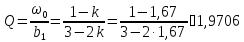
Коэффициент затухания колебательного контура:
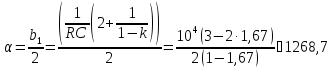
Частота свободных колебаний:
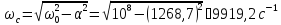
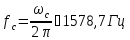
Период свободных колебаний:
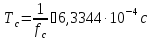
Полюсы операторной передаточной функции:
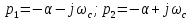
рисунок 2.4.
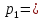
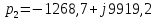
Вывод: поскольку вещественные части полюсов полинома Гурвица отрицательны, цепь устойчива, то есть свободные колебания в ней затухают.
-
Комплексная передаточная функция
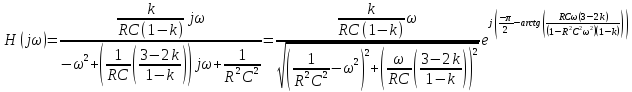
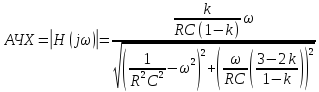
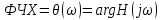
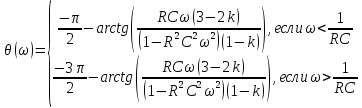
Графики полученных характеристик
график 3.1.
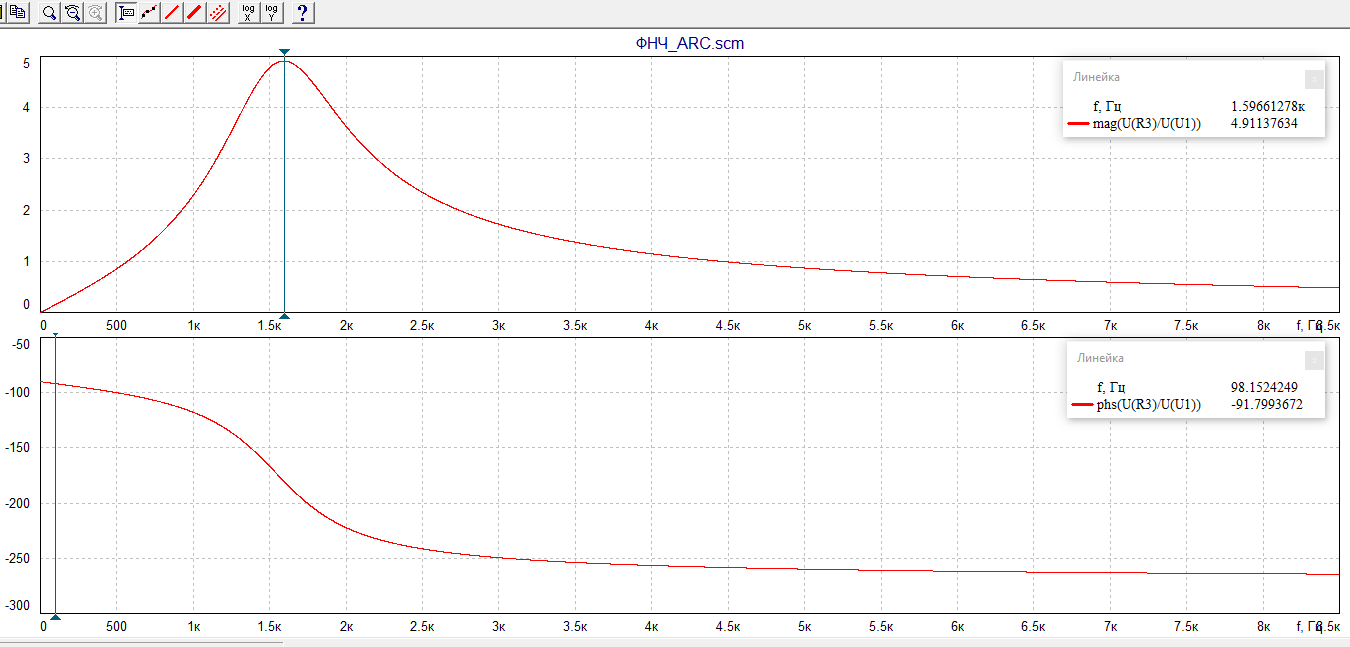
Тип фильтра: полосовой фильтр.
Вычислим:
Значения
АЧХ и ФЧХ фильтра на частотах
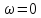 и
и
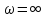
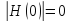
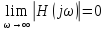
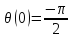
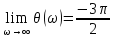
Максимальное значение АХЧ на квазирезонансной частоте
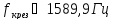
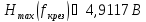
Граничная
частота полосы пропускания фильтра
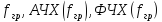
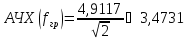
Ширина посолы пропускания:
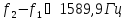
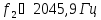
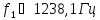
Значения АЧХ, ФЧХ ARC-фильтра, содержащего 6 звеньев 2 порядка
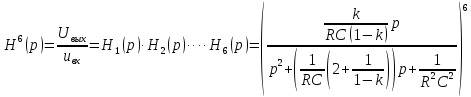
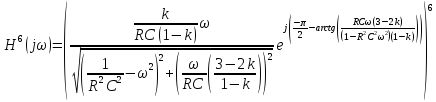
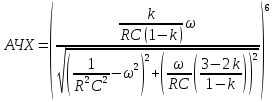
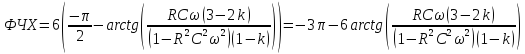
-
Переходная характеристика цепи
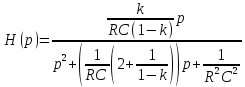
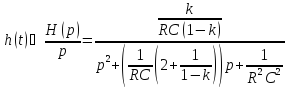
Найдём корни полинома Гурвица v(p):
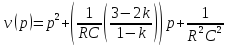
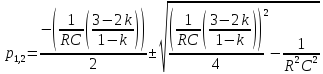
По теореме разложения:
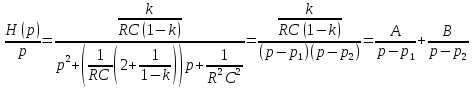
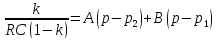
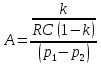
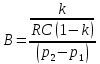
Тогда
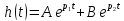
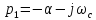
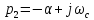
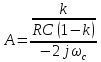
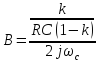
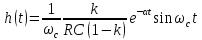
где
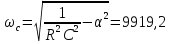 ,
,
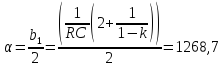
Или в численном виде
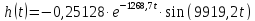
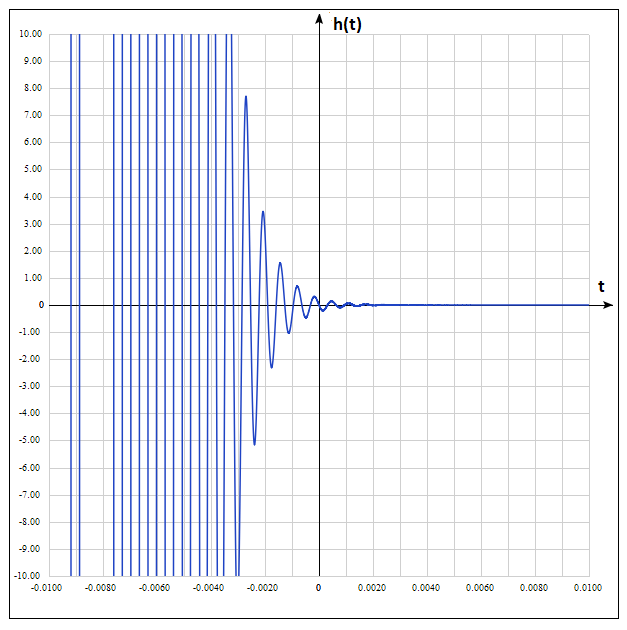
График переходной характеристики показан на рисунке.
график 4.1.
Вычислим:
Декремент затухания свободных колебаний:
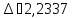
Длительность переходного процесса:
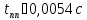
Максимальное значение переходной характеристики:
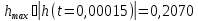
Оценим допустимую величину ступенчатого воздействия на фильтр:
При подаче на вход единичного ступенчатого воздействия (1 В) на выходе максимальное значение становится равным 0,2070 В.
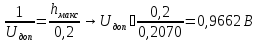
-
Спектральное представление
Комплексная спектральная плотность напряжения на входе:
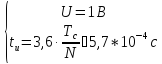
Видеоимпульс прямоугольной формы.
график 5.1.
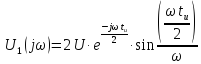
Комплексная спектральная плотность напряжения на выходе цепи:
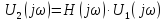
Комплексная передаточная функция имеет вид:
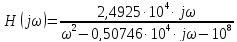
Найдём спектральные характеристики сигналов на входе и выходе ARC-цепи.
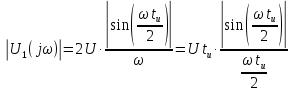
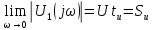
Спектральная плотность амплитуд на выходе цепи равна:
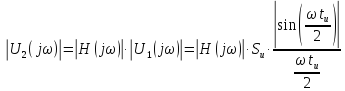
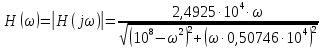
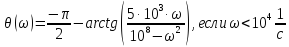
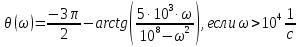
Расчёт
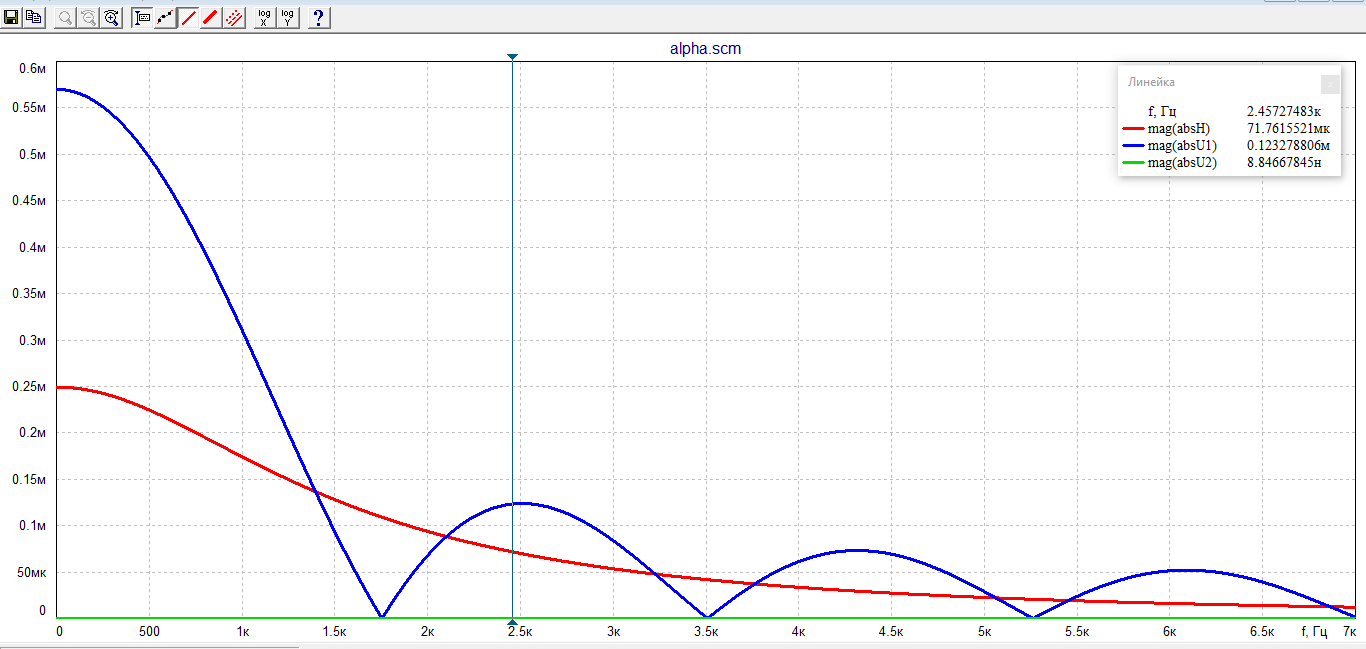
выполним с шагом
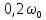 в пределах
в пределах
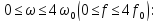
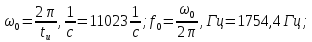
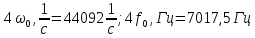
Результаты расчёта приведены в таблице 5.1.
таблица 5.1.
|
|
|
|
|
|
|
|
|
0 |
0,00057 |
0 |
-90 |
0 |
|
|
0,351 |
0,000533 |
0,57362 |
-96,6 |
0,000306 |
|
|
0,702 |
0,000431 |
1,31447 |
-105,3 |
0,000567 |
|
|
1,053 |
0,000288 |
2,51651 |
-120,4 |
0,000724 |
|
|
1,404 |
0,000133 |
4,39871 |
-153,2 |
0,000586 |
|
|
1,754 |
0 |
4,58447 |
-201,3 |
0 |
|
|
2,105 |
0,000089 |
3,27630 |
-228,6 |
0,000291 |
|
|
2,456 |
0,000123 |
2,42209 |
-240,8 |
0,000299 |
|
|
2,807 |
0,000108 |
1,91752 |
-247,3 |
0,000207 |
|
|
3,158 |
0,000059 |
1,59291 |
-251,3 |
0,000094 |
|
|
3,509 |
0 |
1,36719 |
-254,1 |
0 |
|
|
3,860 |
0,000048 |
1,20079 |
-256,0 |
0,000058 |
|
|
4,211 |
0,000072 |
1,07267 |
-257,6 |
0,000077 |
|
|
4,561 |
0,000066 |
0,97070 |
-258,8 |
0,000064 |
|
|
4,912 |
0,000038 |
0,88742 |
-259,7 |
0,000034 |
|
|
5,263 |
0 |
0,81799 |
-260,6 |
0 |
|
|
5,614 |
0,000033 |
0,75913 |
-261,2 |
0,000025 |
|
|
5,965 |
0,000051 |
0,70853 |
-261,8 |
0,000036 |
|
|
6,316 |
0,000048 |
0,66452 |
-262,3 |
0,000032 |
|
|
6,667 |
0,000028 |
0,62586 |
-262,8 |
0,000018 |
|
|
7,018 |
0 |
0,59160 |
-263,2 |
0 |
На рис. 5.2 показаны графики амплитудно-частотной характеристики, спектральных плотностей амплитуд на входе и выходе.
рис 5.2.
-
Разложение на гармоники
Найдём реакцию цепи при подаче на её вход последовательности прямоугольных видеоимпульсов напряжения.
U = 1В;
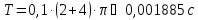
Скважность
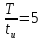
График воздействия с учётом скважности 5 представлен на графике 6.1.
график 6.1.

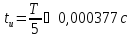
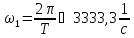

Представим напряжение на входе виде усеченного ряда Фурье
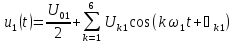
Значения
амплитуд и фаз гармоник напряжения
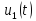 приведены в табл. 6.1.
приведены в табл. 6.1.
таблица 6.1.
|
Номер гармоники k |
||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
|
0,200 |
0,374 |
0,302 |
0,201 |
`0,093 |
|
0,062 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3333 |
6667 |
10000 |
13333 |
16667 |
20000 |
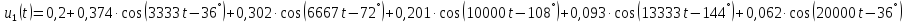
Реакция
цепи на периодическое воздействие
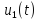 есть сумма реакций на гармонические
составляющие этого воздействия:
есть сумма реакций на гармонические
составляющие этого воздействия:
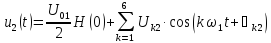
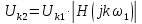
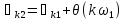
Выражения для амплитудно-частотных характеристик приведены ниже
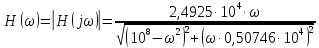
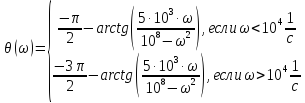
Вычисленные
значения АЧХ, ФЧХ,
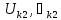 на частотах гармоник входного напряжения
приведены в табл. 6.2.
на частотах гармоник входного напряжения
приведены в табл. 6.2.
таблица 6.2.
|
k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
3333 |
6667 |
10000 |
13333 |
16667 |
20000 |
|
|
|
530,5 |
1 061 |
1 592 |
2 122 |
2 653 |
3 183 |
|
|
0 |
0,91821 |
2,55462 |
4,91172 |
3,22374 |
2,11010 |
1,57403 |
|
|
-90 |
-100,6 |
-121,0 |
-180 |
-229,4 |
-244,9 |
-251,6 |
|
|
0 |
0,34341 |
0,771494 |
0,987255 |
0,299808 |
0 |
0,097590 |
|
|
-90 |
-136,6 |
-193 |
-288 |
-373,4 |
-244,9 |
-287,6 |
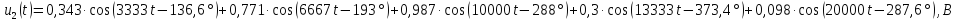
На графике 6.2 представлены графики спектров амплитуд и фаз входного, а на графике 6.3 выходного напряжений.
график 6.2.а)
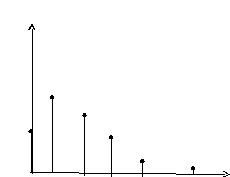
график 6.2.б)
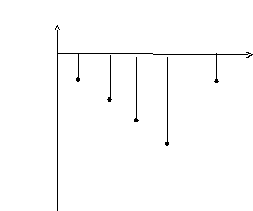
график 6.3.а)
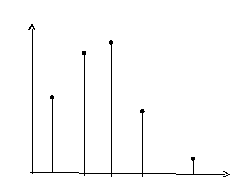
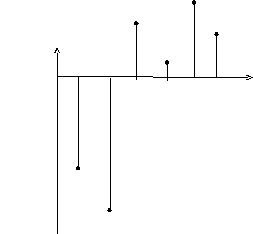 график
6.3.б)
график
6.3.б)
САНКТ-ПЕТЕРБУРГ 2018

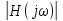
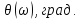
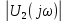
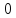
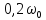
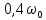
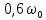
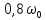
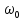
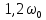
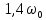
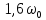
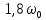
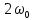
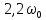
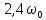
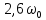
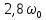
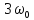
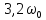
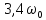
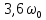
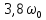
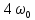
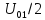
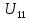
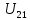
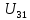
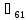
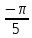
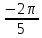
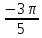
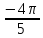
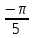
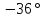
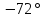
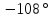
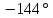
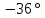
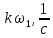
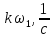
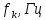
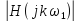
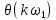 ,
град.
,
град.