4.2 Головний вектор і головний момент сил інерції
4.2.1 Тіло масою m = 20 кг рухається поступально з пришвидшенням 20 м/с2. Визначити модуль головного вектора сил інерції.
|
а) 50 Н; б) 100 Н;
в) 250 Н0
Н ковзання чки, якщо коєо
коєфіціточки г) 300 Н; д) 400 Н. |
|
4.2.2 Кривошип ОА довжиною 0,1 м шарнірного паралелограма ОАВС починає обертатися із стану спокою з постійним кутовим пришвидшенням = 2 рад/с2. Визначити модуль рівнодійної сил інерції стрижня АВ масою 2 кг в момент часу t = 1 с.
|
а) 0,894 Н; б) 1,348 Н;
в) 2,438 Н0
Н ковзання чки, якщо коєо
коєфіціточки г) 3,119 Н; д) 4,001 Н. |
|
4.2.3 Водило 1 довжиною l = 0,8 м планетарного механізму обертається з постійним кутовим пришвидшенням =10 рад/с2. Колесо 2 масою m = 2 кг при цьому рухається поступально. Центр мас колеса 2 збігається з точкою О1 . Визначити головний момент сил інерції колеса 2 відносно центра О.
|
а) 7,3 Нм; б) 12,8 Нм;
в) 24,3 Нм0
Н ковзання чки, якщо коєо
коєфіціточки г) 38,1 Нм; д) 42,7 Нм. |
|
4.2.4 Визначити головний момент сил інерції колеса відносно центра мас О, якщо колесо обертається навколо нього за законом = 2t2(рад), а маса колеса m = 2 кг і рівномірно розподілена по ободу радіусом R=20 см.
|
а) 0,01 Нм; б) -0,15 Нм;
в) -0,32 Нм0
Н ковзання чки, якщо коєо
коєфіціточки г) -0,45 Нм; д) -0,81 Нм. |
|
4.2.5 Визначити головний момент сил інерції однорідного колеса радіусом R=0,2 м відносно осі обертання OZ, що проходить через центр мас колеса О в момент часу t = 1 с, якщо закон обертання має вигляд
= 3t3-5t2 (рад), а маса колеса m = 10 кг.
|
а) 0,2 Нм; б) 0,8 Нм;
в) -1,6 Нм;0
Н ковзання чки, якщо коєо
коєфіціточки г) -2,3 Нм; д) 3,1 Нм. |
|
4.2.6 Однорідний циліндр радіусом R=0,15 м і масою 40 кг обертається навколо осі OZ з кутовою швидкістю =50t (рад/с). Визначити головний момент сил інерції циліндра відносно осі обертання.
|
а) 8,7 Нм; б) 12,1 Нм;
в) 16,4 Нм0
Н ковзання чки, якщо коєо
коєфіціточки г) 22,5 Нм; д) 31,1 Нм. |
|
4.2.7 Колесо масою m = 0,3 кг з радіусом інерції =0,1 м обертається відносно осі OZ за законом =25t2(рад). Визначити головний момент сил інерції колеса відносно осі обертання.
|
а) 0,15 Нм; б) 0,45 Нм;
в) 0,67 Нм0
Н ковзання чки, якщо коєо
коєфіціточки г) 1,31 Нм; д) 2,46 Нм. |
|
4.2.8 Тонкий однорідний стрижень АВ масою m=1кг і розмірами вказаними на рисунку, обертається з постійною кутовою швидкістю = 5 рад/с навколо осі, перпендикулярної стрижню. Визначити модуль головного вектора сил інерції стрижня .
|
а) 0,4 Н; б) 2,5 Н ;
в) 4,2 Н0 Н ковзання
чки, якщо коєо
коєфіціточки г) 6,1 Н; д) 8,6 Н. |
|
4.2.9 Визначити головний момент сил інерції однорідного диска радіусом r = 0,2 м і масою m = 2 кг відносно осі обертання Оz, що зміщена на відстань е = 0,1 м від центра мас С. Диск обертається з кутовим пришвидшенням =10 рад/с2.
|
а) 0,1 Нм; б) 0,2 Нм;
в) 0,6 Нм0
Н ковзання чки, якщо коєо
коєфіціточки г) 1,2 Нм; д) 2,4 Нм. |
|
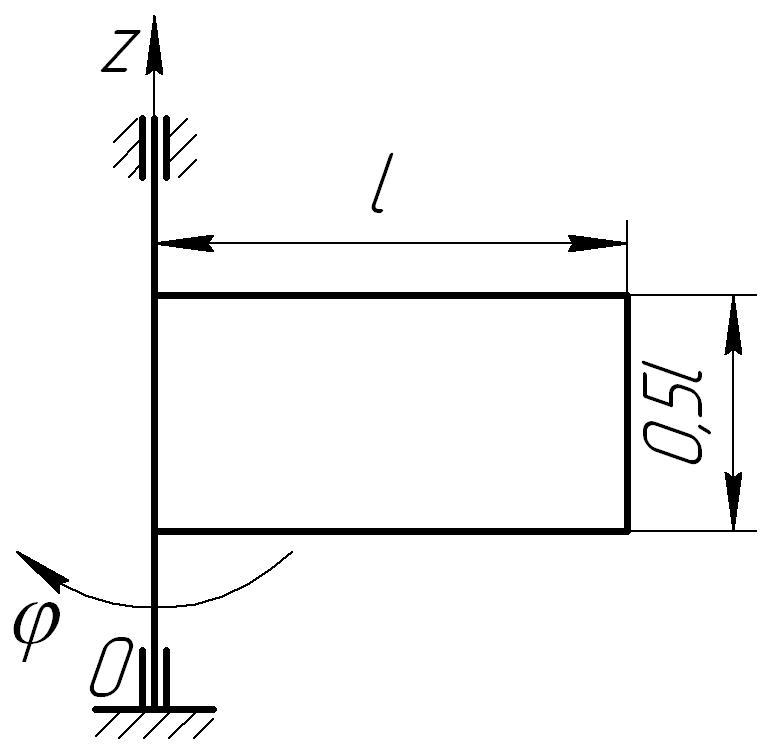
4.2.10 Однорідна прямокутна пластина масою m=1кг обертається з кутовим пришвидшенням =30рад/с2 навколо осі, перпендикулярної площині пластини. Визначити головний момент сил інерції відносно осі обертання, якщо l = 0,1 м.
|
а) - 0,01 Нм; б) -0,15 Нм;
в) -0, 12 Нм0
Н ковзання чки, якщо коєо
коєфіціточки г) -0,50 Нм; д) 1,00 Нм. |
|
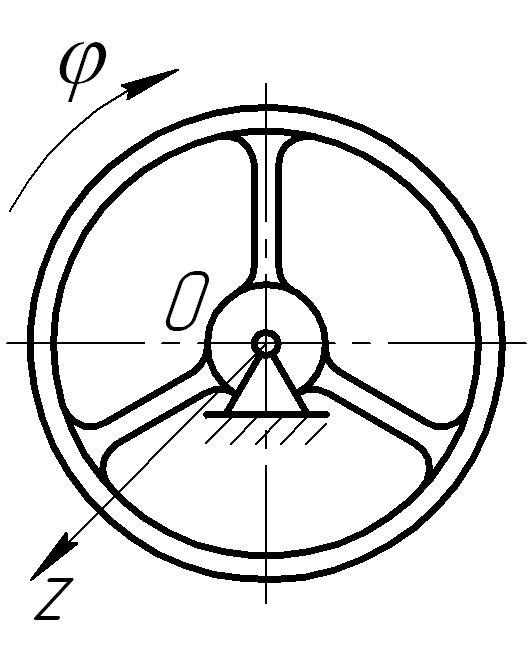
4.2.11 Однорідна кругла пластина масою m = 1 кг обертається з кутовим пришвидшенням =20 рад/с2 навколо осі, перпендикулярної площині пластини. Визначити головний момент сил інерції відносно осі обертання, якщо R = 0,1 м.
|
а) - 0,01 Нм; б) -0,05 Нм;
в) -0, 20 Нм0
Н ковзання чки, якщо коєо
коєфіціточки г) -0,25 Нм; д) -0,30Нм. |
|
4.2.12 Однорідна прямокутна пластина масою m=3кг обертається навколо осі Оz за законом = 3t2(рад). Визначити головний момент сил інерції пластини відносно осі Оz, якщо l = 0,1 м.
|
а) 0,06 Нм; б) 0,10 Нм;
в) 0,16 Нм0
Н ковзання чки, якщо коєо
коєфіціточки г) 0,26 Нм; д) 0,35 Нм. |
|
4.2.13 Однорідний циліндр радіуса r =0,2 м котиться по площині. Визначити головний момент сил інерції відносно точки А, якщо маса циліндра m = 5кг, а пришвидшення його центра мас а = 4 м/с2.
|
а) 6 Нм; б) 10 Нм;
в) 14 Нм0
Н ковзання чки, якщо коєо
коєфіціточки г) 18 Нм; д) 25 Нм. |
|
4.2.14 Однорідний циліндр
масою m = 10 кг
котиться по площині за законом
,
де
– в м. Визначити модуль головного
вектора сил інерції циліндра в момент
часу t =
1 с.
|
а) 0,114 Н; б) 0,436 Н;
в) 0,646 Н0
Н ковзання чки, якщо коєо
коєфіціточки г) 0,836 Н; д) 1,036 Н. |
|
4.2.15 Однорідний циліндр масою m
= 10 кг і радіусом r
=0,1 м котиться по площині за законом
,
де
– в м. Визначити головний момент сил
інерції циліндра в момент часу t
= 1 с відносно центра мас циліндра.
|
а) 0,001 Нм; б) 0,028 Нм;
в) 0,218 Нм0
Н ковзання чки, якщо коєо
коєфіціточки г) 0,536 Нм; д) 0,946 Нм. |
|
4.2.16 Однорідний диск радіусом r1 =12 см масою m=10 кг котиться по поверхні радіусом r2 =20 см. Центр О1 диска переміщається за законом S = 50t2, де S – в см. Визначити модуль головного вектора сил інерції диска в момент часу t = 1 с.
|
а) 1,3 Н; б) 11,1 Н;
в) 21,3 Н0 Н ковзання
чки, якщо коєо
коєфіціточки г) 32,8 Н; д) 48,3 Н. |
|
4.2.17 Однорідний циліндр радіусом r = 0,24 м і масою m = 20 кг котиться по сферичній поверхні. Пришвидшення центра О циліндра а = 60 м/с2. Визначити головний момент сил інерції циліндра, приймаючи за центр зведення точку А.
|
а) 18 Нм; б) 36 Нм;
в) 87 Нм0
Н ковзання чки, якщо коєо
коєфіціточки г) 147 Нм; д) 216 Нм. |
|
4.2.18 Кривошип 1 обертається з постійною кутовою швидкістю =4 рад/с і приводить в рух однорідне колесо 2 масою m = 4 кг, що котиться по внутрішній поверхні колеса 3. Визначити модуль головного вектора сил інерції колеса 2 за умови, що R = 40 см, r = 15 см.
|
а) 16 Н; б) 38 Н;
в) 46 Н0 Н ковзання
чки, якщо коєо
коєфіціточки г) 58 Н; д) 64 Н. |
|
4.2.19 Однорідний стрижень, довжиною АВ = 50 см і масою m = 10 кг рухається в площині Оху за рівняннями: ХА = 4t2м; УА = 0; = 6t2 рад. Визначити головний момент сил інерції стрижня відносно його центра мас.
|
а) -2,5 Нм; б) -6,1 Нм;
в) -16,3 Нм0
Н ковзання чки, якщо коєо
коєфіціточки г) -18,1 Нм; д) -24,3 Нм |
|
