
- •Рецензент: Писаренко э.В.
- •Введение
- •Алгоритмизация
- •1. Вычисление суммы (суммирование) элементов вектора
- •2. Вычисление произведения элементов вектора
- •Пример 3
- •3. Вычисление произведения двух векторов
- •4. Суммирование (вычитание) матриц
- •5. ВычислениЕ произведения матриц
- •6. Вычисление произведения матрицы на вектор
- •7. Вычисление единичной матрицы
- •8. Транспонирование матрицы
- •Aij пустая ячейка b aji
- •9. Инвертирование элементов вектора
- •10. Алгоритм поиска максимального ( или минималь-ного ) элемента вектора
- •11. Алгоритм сортировки (упорядочивания) элементов вектора или матрицы
- •12. Вычисление полинома по схеме горнера
- •13. Вычисление суммы членов ряда
- •Содержание
8. Транспонирование матрицы
Транспонирование
матрицы A={![]() }N*N
предполагает
перестановку в ней элементов строк и
столбцов.
}N*N
предполагает
перестановку в ней элементов строк и
столбцов.
Например, A=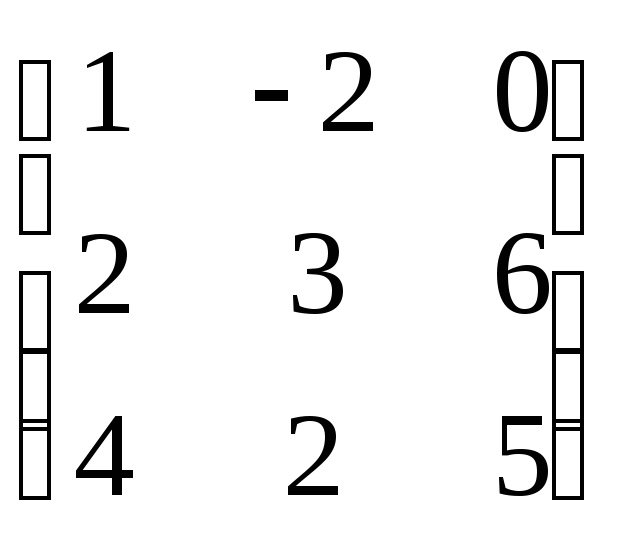 ,
тогда AT
=
,
тогда AT
=
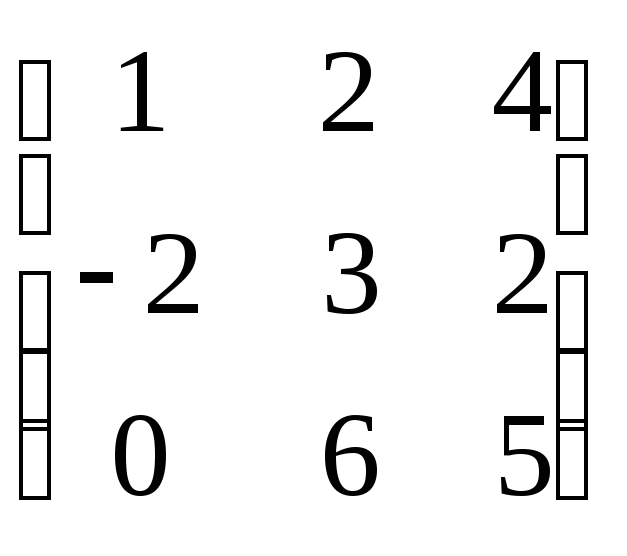 . (
16 )
. (
16 )
Существуют два способа решения данной задачи:
-
с использованием новой матрицы AT={
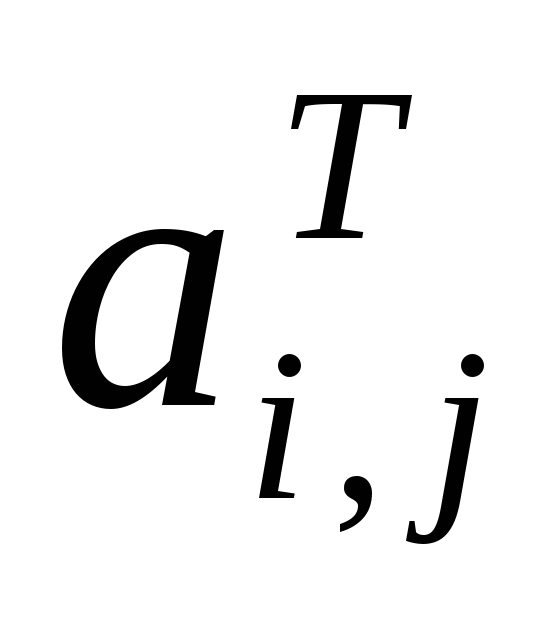 }N*N
,
}N*N
,
в этом случае
![]() для
для
![]() ;
;
-
путем перестановки в три шага соответствующих элементов в исходной матрице A (рис.18).
2

 -ой
шаг
-ой
шаг
1 -ый
шаг 3-ий шаг
-ый
шаг 3-ий шаг
Aij пустая ячейка b aji
Рис.18
Схемы алгоритмов транспонирования элементов матрицы для обоих способов показаны на рис. 19.
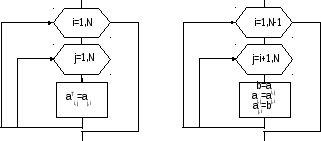
1) 2)
Рис. 19
9. Инвертирование элементов вектора
Инвертирование
вектора X={![]() }N
означает перечисление элементов вектора
в обратном порядке. Например, если X=(0,
-3, 2, 6), тогда XIN
= (6, 2, -3,
0) .
}N
означает перечисление элементов вектора
в обратном порядке. Например, если X=(0,
-3, 2, 6), тогда XIN
= (6, 2, -3,
0) .
Аналогично, существуют два способа решения данной задачи:
1) с использованием
нового вектора XIN={![]() }N
,
}N
,
в этом случае
![]() =
=![]() для
для
![]() ;
;
2) путем перестановки в три шага соответствующих элементов в исходном векторе X .
Схемы алгоритмов способов инвертирования элементов вектора пред-ставлены на рис. 20.

1) 2)
Рис. 20
Рассмотрим более сложную задачу.
Пример 7
Необходимо вычислить значение параметра Z в соответствии со следующим выражением:
Z = ( A - E ) * C1IN * ( C22 - 1 ) , ( 17 )
где A - исходная матрица, все элементы и размерность которой известны;
E – единичная матрица;
C1 – главная диагональ матрицы A;
C2 – побочная диагональ матрицы A.
Рассмотрим поэтапный процесс решения данной задачи.
-
Ввод размерности N и всех элементов матрицы
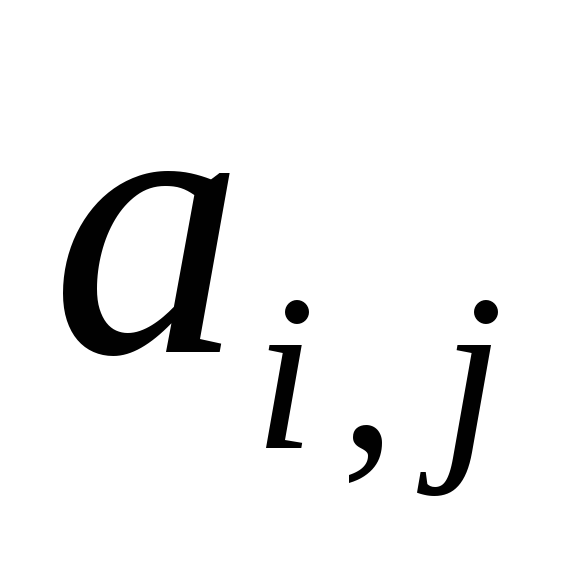 (
(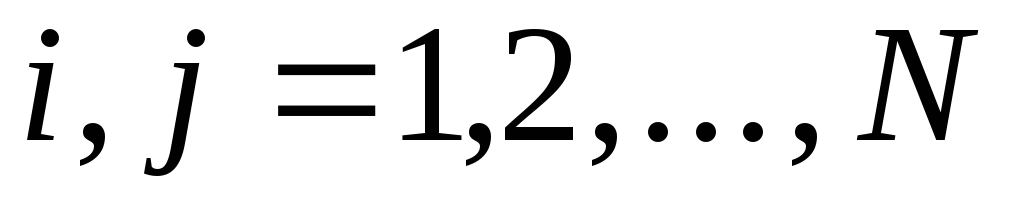 ).
). -
Вычисление единичной матрицы E={
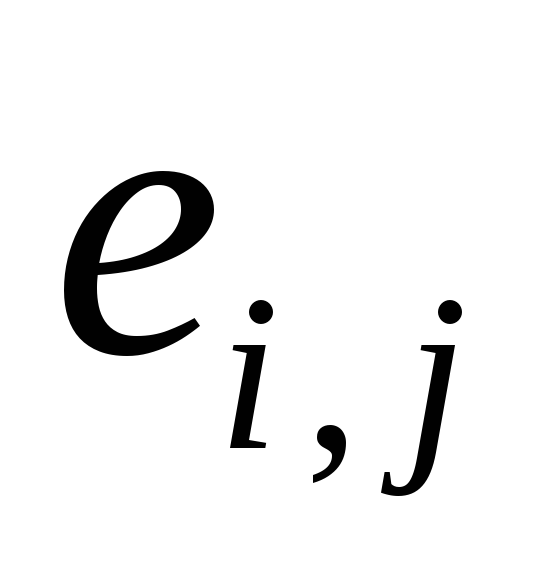 }N*N.
}N*N. -
Вычисление главной диагонали (вектор)
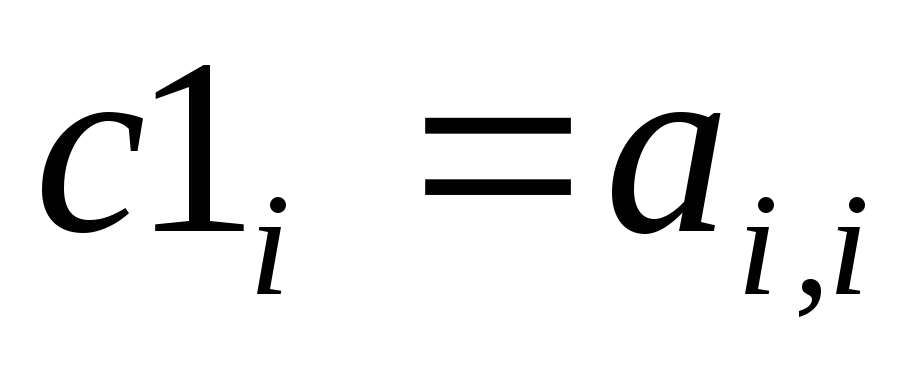 (
(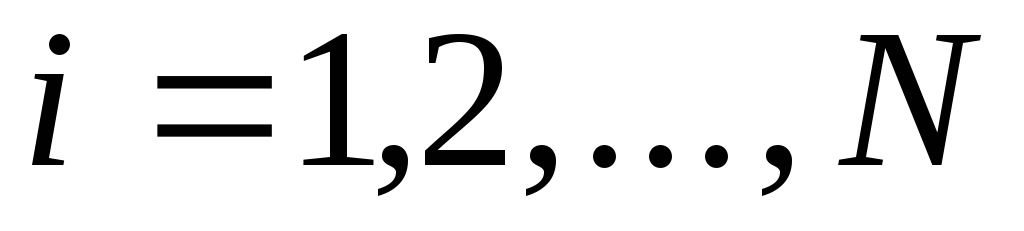 ).
). -
Вычисление побочной диагонали (вектор)
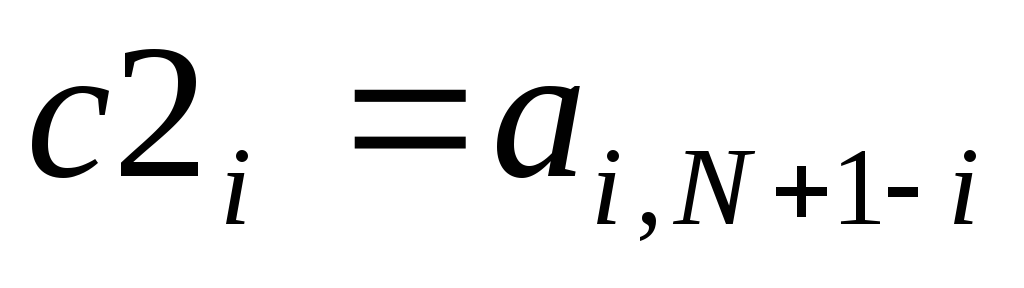 (
(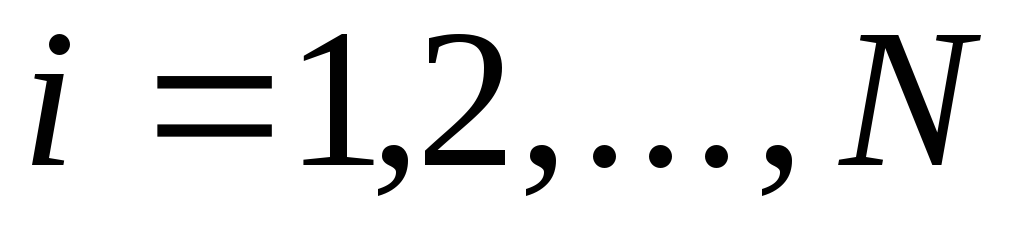 ).
). -
Инвертирование вектора C1:
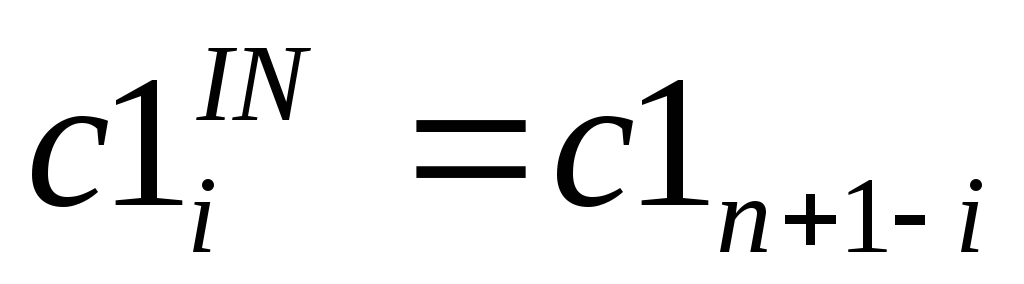 (
(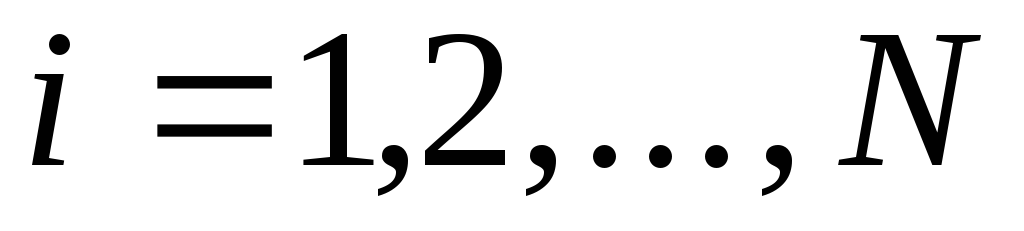 ).
). -
Вычисление квадратной матрицы B=A-E.
-
Вычисление вектора D=B*C1IN.
-
Вычисление значения F=C2*C2.
-
Вычисление значения K=F-1.
-
Вычисление вектора Z=D*K.
-
Вывод вектора Z={
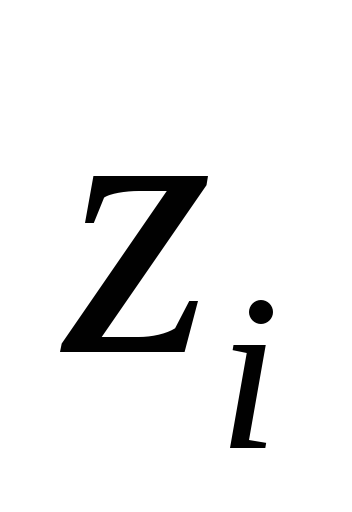 }N.
}N.
Алгоритмы для каждого этапа процедуры вычислений рассмотрены выше, за исключением очевидного десятого пункта.
В процессе программирования достаточно сложных задач, подобных примеру 7, необходимо учесть следующие рекомендации:
1) предусмотреть комментарии к каждому пункту задачи;
2) организовать вывод значений рассчитанных параметров при выпол-нении каждого пункта задачи.
Данные рекомендации способствуют лучшему пониманию и контролю процесса поэтапных вычислений.
10. Алгоритм поиска максимального ( или минималь-ного ) элемента вектора
Дан вектор X={![]() }N
.
}N
.
Необходимо найти
элемент вектора Х
, имеющий максимальное значение. Например,
пусть X
= (3, 4, 2, -1, 6,
0). Очевидно, что M(max)
=![]() =
6; L
(порядковый номер максимального
элемента)=5.
=
6; L
(порядковый номер максимального
элемента)=5.
Процедура поиска максимального элемента вектора следующая: предположим, что максимальным является первый элемент, т.e. M=Х1, L=1.
|
Алгоритм поиска максимального элемента вектора показан на рис. 21. Данный алгоритм пригоден для поиска минимального элемента вектора при очевидной замене знака "<" на знак ">" в блоке проверки условия (рис. 21).
|
Рис. 21 |

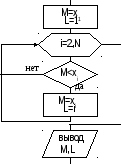 Затем
каждый элемент
Затем
каждый элемент