
- •Рецензент: Писаренко э.В.
- •Введение
- •Алгоритмизация
- •1. Вычисление суммы (суммирование) элементов вектора
- •2. Вычисление произведения элементов вектора
- •Пример 3
- •3. Вычисление произведения двух векторов
- •4. Суммирование (вычитание) матриц
- •5. ВычислениЕ произведения матриц
- •6. Вычисление произведения матрицы на вектор
- •7. Вычисление единичной матрицы
- •8. Транспонирование матрицы
- •Aij пустая ячейка b aji
- •9. Инвертирование элементов вектора
- •10. Алгоритм поиска максимального ( или минималь-ного ) элемента вектора
- •11. Алгоритм сортировки (упорядочивания) элементов вектора или матрицы
- •12. Вычисление полинома по схеме горнера
- •13. Вычисление суммы членов ряда
- •Содержание
1. Вычисление суммы (суммирование) элементов вектора
Для вычисления
суммы
![]() элементов
вектора, предположим, X
= {
элементов
вектора, предположим, X
= {![]() },
i
= 1, 2, ..., N,
его значения и размерность N
должны быть
известны как
для данного случая, так и для последующих
задач.
},
i
= 1, 2, ..., N,
его значения и размерность N
должны быть
известны как
для данного случая, так и для последующих
задач.
|
Очевидно,
Алгоритм суммирования элемен-тов вектора приведен на рис. 5.
Отметим, что
начальное значение суммы
Покажем, как можно использовать данный типовой алгоритм для реше-ния более сложной задачи.
|
Рис.5 |
|
Необходимо
вычислить средне- арифметическое
значение
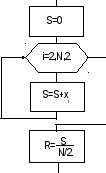
Алгоритм примера 2 показан на рис. 6.
|
Рис.6 |
2. Вычисление произведения элементов вектора

|
Очевидно,
Алгоритм для вычисления произведения элементов вектора приведен на рис. 7.
Отметим, что
начальное значение произве-дения
|
Рис.7 |
Пример 3
Н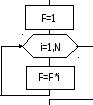 еобходимо
вычислить значение произведения
еобходимо
вычислить значение произведения
![]() (факториала)
натурального ряда целых чисел от 1 до
N.
(факториала)
натурального ряда целых чисел от 1 до
N.
|
Следовательно,
Схема алгоритма
для вычисления факто-риала
|
Рис.8 |
Пример 4
Необходимо
вычислить среднегеометрическое значение
Q
положитель-ных элементов вектора
C
=
{![]() },
},
![]() .
При формализации данной задачи приходим
к следующему выражению:
.
При формализации данной задачи приходим
к следующему выражению:
![]() , (
5 )
, (
5 )
где k
– число положительных элементов
![]() <
0.
<
0.
Эта задача может быть решена методом “сверху вниз”, как показано на рис. 9.

Рис. 9
Окончательная схема алгоритма решения данной задачи показана на рис. 10.
Р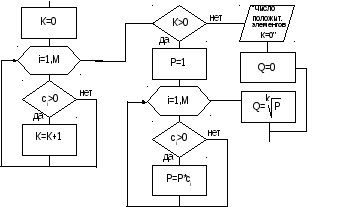 ис.10
ис.10
Пример 5
Дан вектор X
= {![]() },
i=1,
2, ..., N.
Необходимо вычислить значение Р согласно
следующему выражению:
},
i=1,
2, ..., N.
Необходимо вычислить значение Р согласно
следующему выражению:
P
=
![]()
![]() k.
( 6 )
k.
( 6 )
Например, если N = 4 тогда
P
=
![]()
Графическая схема алгоритма данной задачи представлена на рис. 11.

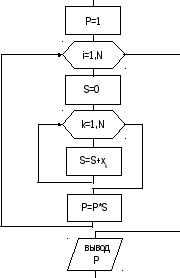



Вычисление
суммы
S=
![]()

Рис.11
3. Вычисление произведения двух векторов
|
i=1, 2, ..., N . Отметим, что размер обоих векторов равен N, а результатом произве-дения двух векторов будет число
C
= A
*
B
=
Алгоритм вычисления произведения двух векторов приведен на рис. 12. |
Рис. 12 |
Пример 6
Дана матрица A
= {![]() }
, i,
j=1,
2, ..., N.
}
, i,
j=1,
2, ..., N.
Необходимо вычислить
элементы вектора X
= {![]() },
i=1,
2, ... , N.
Каждый элемент вектора
},
i=1,
2, ... , N.
Каждый элемент вектора
![]() вычисляется
как произведение i-го
столбца и главной диагонали матрицы A.
вычисляется
как произведение i-го
столбца и главной диагонали матрицы A.
Например, пусть N = 3 и известны все элементы матрицы A
A
=
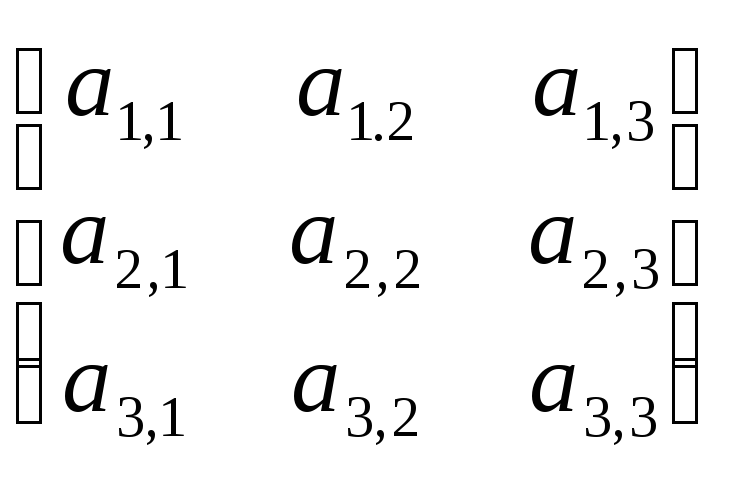 =
=
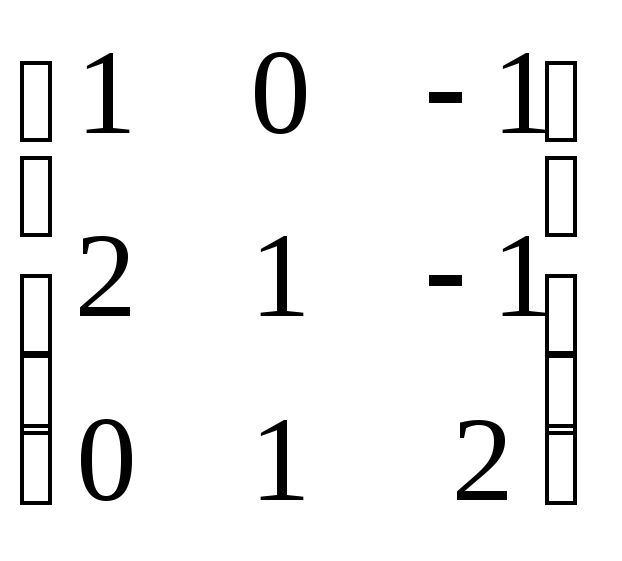 .
.
Попутно отметим, что i-ая строка, j-ый столбец, главная и побочная диагонали матрицы A по сути является вектором.
Действительно,
![]() - 2-ая
строка (вектор),
- 2-ая
строка (вектор),
![]() - 3-ий
столбец (вектор),
- 3-ий
столбец (вектор),
![]() {
{![]() }N - главная
диагональ (вектор),
}N - главная
диагональ (вектор),
![]() {
{![]() }N - побочная
диагональ (вектор).
}N - побочная
диагональ (вектор).
В соответствии с условием задачи (пример 6), элементы вектора xi могут быть рассчитаны следующим образом:
для ![]()
![]() =
=![]() *
*![]() +
+![]() *
*![]() +
+![]() *
*![]() =
=![]()
![]() ;
;
для ![]()
![]() =
=![]() ;
;
для ![]()
![]() .
.
Формализация данной задачи приводит к следующему выражению:
![]() ,
i
= 1, 2, . . . , N (
8 )
,
i
= 1, 2, . . . , N (
8 )
Два варианта разработки алгоритма данной задачи показаны на рис. 13.
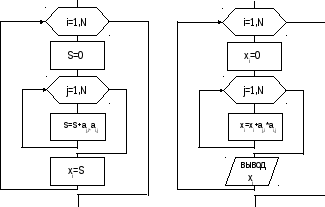
Рис.13


 Пример
2
Пример
2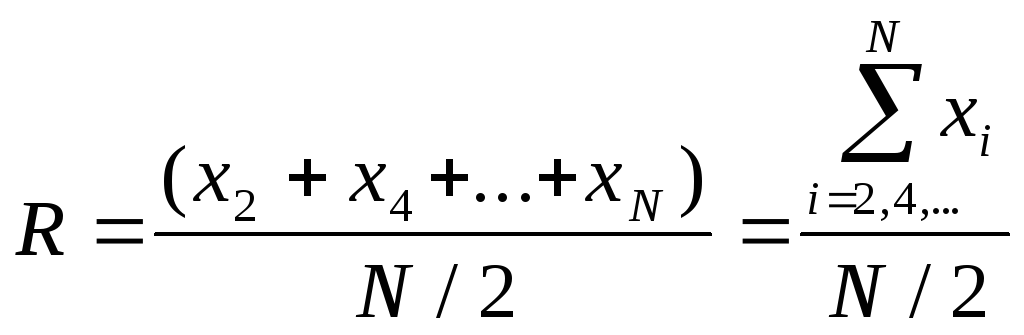 ( 2 )
( 2 )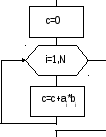 Даны
два вектора
A
= {ai}
и B
= {bi},
Даны
два вектора
A
= {ai}
и B
= {bi},
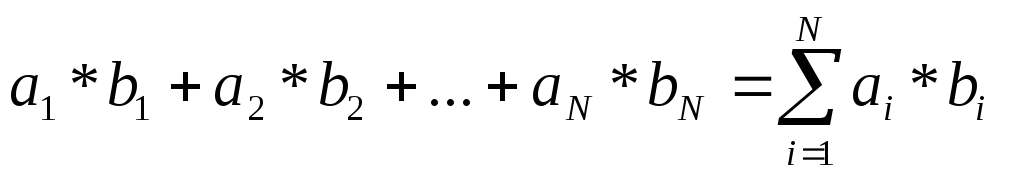 (7)
(7)