Задание для самостоятельной аудиторной работы

1. В соответствии с вариантом (таблица 1) определите физические величины, приведенные в таблицы 2.

Таблица 1

Вариант	С, Дж/°С	Л, Дж/с ·°С	Р, Вт	,°С	,°С
1	360000	200	5000	-5	12
2	400000	400	10000	-8	10
3	300000	300	7500	-10	12
4	400000	500	12500	-4	14
5	250000	150	3750	-6	10
6	300000	350	8750	-9	12
7	360000	200	5000	5	12
8	400000	400	10000	8	10
9	300000	300	7500	10	12
10	400000	500	12500	4	14
11	250000	150	3750	6	10
12	300000	350	8750	9	12

Таблица 2

Т, с	,°С	,°С	,°С	tдоп, с
		25

Комплексная общенаучная задача 2.

2.1 Производственно-техническая ситуация.

Электромагнитная шайба для подъема металлолома в своей конструкции имеет намагничивающую катушку. Потребовалось исследовать процесс намагничивания шайбы во времени, который определяется намагничивающим током, потребляемым катушкой шайбы. Было составлено следующее условие для анализа процесса намагничивания.

К источнику постоянного тока, электродвижущая сила которого равна 100 В, мгновенно подключается катушка с известными параметрами: активным сопротивлением 6 Ом, индуктивностью катушки 1,2 Гн.

2.2 Разрешение производственно-технической ситуации.

Приводим последовательность Ваших рассуждений и действий по разрешению производственно – технической ситуации.

Прежде всего Вы составили себе алгоритм разрешения производственно-технической ситуации:

1. Записать условие, введя буквенные обозначения указанных в условии величин.

2. Составить дифференциальное уравнение электрической цепи, введя обозначение тока в цепи после коммутации (включения) () и времени ().

3. Найти закон изменения тока в цепи в функции времени ().

4. Составить программу расчета тока в цепи в функции времени (на микрокалькуляторе или ЭВМ).

5. Рассчитать график изменения тока в функции времени и результаты занесите в таблицу.

6. Построить график . Найдите графически постоянную времени цепи, сравните ее с расчетным значением.

Затем Вы приступили к выполнению алгоритма разрешения производственно-технической ситуации:

1. Составили условие задания:

2. Составляем дифференциальное уравнение электрической цепи, введя обозначение тока в цепи после коммутации (включения) () и времени ().

где – постоянное напряжение на зажимах цепи, В;

– индуктивность катушки, Гн;

– активное сопротивление катушки, Ом;

– сила электрического тока в катушке, А.

2. Нашли закон изменения тока в цепи в функции времени (), решив дифференциальное уравнение цепи.

Преобразовали уравнение:

Ввели условные обозначения:

Назвали Т постоянной времени цепи, единицей является секунда.

Назвали установившимся значением силы электрического тока.

Переписали уравнение с учетом введенных обозначений:

Решили полученное дифференциальное уравнение, для чего составили характеристическое уравнение:

откуда нашли корень:

Сила электрического тока будет содержать свободную и принужденную составляющие, то есть

Свободная составляющая определяется корнем характеристического уравнения и запишется следующим образом:

где А – постоянная интегрирования.

Принужденная составляющая равна установившемуся значению силы электрического тока, то есть

Тогда общее решение дифференциального уравнения записали следующим образом

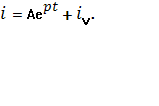
Нашли постоянную интегрирования из начальных условий:

при .

Тогда ,

откуда .

Подставили значение постоянной интегрирования в общее решение дифференциального уравнения и получили искомый закон изменения силы электрического тока:

Представили эту зависимость от графически (рис. 1).

4. Составили алгоритм расчета силы электрического тока во времени:

• определяем значение постоянной времени цепи:

• определяем значение установившейся силы электрического тока:

• задаемся значениями отрезков времени кратным и находим для этих значений ;

• рассчитываем силу электрического тока в конце каждого очередного отрезка времени, то есть при значениях времени и так далее, используя уравнение

Составили программу расчета силы электрического тока на микрокалькуляторе или ЭВМ.

5. Рассчитали график изменения тока в функции времени :

Таблица 1.

	0	0,02	0,04	0,06	0,08	0,1	0,12	0,14	0,16	0,18	0,2
	1	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
	1	0,905	0,818	0,741	0,67	0,60	0,549	0,497	0,449	0,407	0,368
	0	0,15	0,16	0,44	0,56	0,66	0,77	0,86	0,94	1,01	1,07

6. Построили график силы электрического тока (рис. 2).

Определили графически путем постоянную времени цепи Т. Значение совпало с расчетным значением и равно 0,2 с.

Как видно из графика, значение постоянной времени нагрева Т, найденное графическим путем, равно 0,2 с, что соответствует расчетному значению.