Глава 9 Производящие функции

При доказательстве тех или иных комбинаторных тождеств часто используется одно или одновременно два из следующих правил:

Правило суммы. Если объект А может быть выбран m способами, а объект В другими n способами, то выбор “либо А, либо В” может быть осуществлен m+n способами.

Правило произведения. Если объект А может быть выбран m способами и после каждого из таких выборов объект В в свою очередь может быть выбран n способами, то выбор “А, и В” в указанном порядке может быть осуществлен mn способами.

Примеры. На основе этих правил в курсе математического анализа легко были получены формулы для числа k-перестановок и числа k-сочетаний из n объектов, а именно

= n(n-1)…(n-k+1)

=

Упражнение. Докажите, что число k-перестановок из n объектов с повторениями равно n^k.

Задача. Доказать, что число k-сочетаний из n объектов с повторениями равно .

Решение (Л. Эйлер): Пусть X={1,2,…n} и рассмотрим любое из k-сочетаний с повторениями с₁с₂…с_k этих n чисел (считаем, что в сочетании с₁с₂…с_k элементы выписаны в неубывающем порядке). Естественно, что в каждом сочетании вследствие возможности неограниченных повторений любые рядом стоящие элементы могут быть одинаковыми. Ввиду этого обстоятельства строим с помощью соотношений

d₁=c₁+0; d₂=c₂+1;…; d_i=c_i+i-1;…; d_k=c_k+k-1

последовательность элементов d₁d₂…d_k следовательно, при любых элементах c_i элементы d_i всегда различны. Ясно, что отображение с₁с₂…с_k в d₁d₂…d_k биективно. Число последовательностей из элементов d_i равно числу k-сочетаний без повторений из элементов от 1 до n+k-1, т. е. .

Производящие функции для сочетаний.

Для примера рассмотрим три объекта, обозначенные x₁, x₂, x₃. Образуем произведение

(1+x₁t)(1+ x₂t)(1+x₃t).

Перемножив и разложив это произведение по степеням t, получим

1+(x₁+x₂+x₃)t+(x₁x₂+x₁x₃+x₂x₃)t²+x₁x₂x₃t³,

или

1+а₁t+а₂t²+а₃t³,

где а₁, а₂, а₃ – элементарные симметрические функции трех переменных x₁, x₂, x₃. Эти симметрические функции определяются вышеприведенным выражением. Можно заметить, что число слагаемых каждого коэффициента а_m (m=1,2,3) равно числу сочетаний из трех элементов по k. Следовательно, число таких сочетаний получается приравниванием каждого x_i единице, т. е.

(1+t)³=

Для случая n различных объектов, обозначенных x₁, . . . , x_n ясно, что

(1+x₁t)(1+ x₂t) . . . .(1+x_nt)=

=1+a₁(x₁,. . ., x_n)t+ a₂(x₁,. . ., x_n)t²+. . .+ a_n(x₁,. . ., x_n)tⁿ

и

(1+t)ⁿ==;

поэтому выражение (1+t)ⁿ называют перечисляющей функцией сочетаний из n различных объектов. Этот результат можно также обосновать следующими комбинаторными рассуждениями:

В произведении (1+x₁t)(1+ x₂t) . . . .(1+x_nt) каждый множитель является биномом, который благодаря наличию в нем слагаемых 1 и x_i указывает на возможность наличия или отсутствия в каждом из сочетаний элемента x_i. Это произведение порождает сочетания, так как коэффициент при t^m в нем получается выбором “1” в n-m из n двучленных множителей и в m оставшихся после такого выбора множителях - членов вида x_it всеми возможными путями. Эти коэффициенты по самому их определению являются m-сочетаниями. Каждый элемент в любом сочетании может появляться не более одного раза, ибо любой множитель состоит только из двух слагаемых.

Обобщая эти комбинаторные рассуждения, для случая, когда прежние множители вида 1+x_it заменяются множителями вида 1+xt+xt²+ … +xt^j, построим производящую функцию для сочетаний, в которых элементы x_i могут содержаться 0,1,2,…,j раз. Более того, множители производящей функции можно совершенно независимо друг от друга приспосабливать к любым требованиям задачи. Так, например, если x_k должно всегда входить четное число раз, но не более чем 2k раз, то k-й множитель следует выбирать в виде

1+xt+xt⁴+ … +xt^2k .

Таким образом, производящая функция для любой задачи описывает не только виды элементов, но и виды искомых сочетаний.

Пример. Для сочетаний с неограниченным повторением элементов n и без ограничения на число появлений любого элемента перечисляющей производящей функцией будет

(1+t+t²+. . .)ⁿ

или, что же самое

(1-t)^-n = ==.

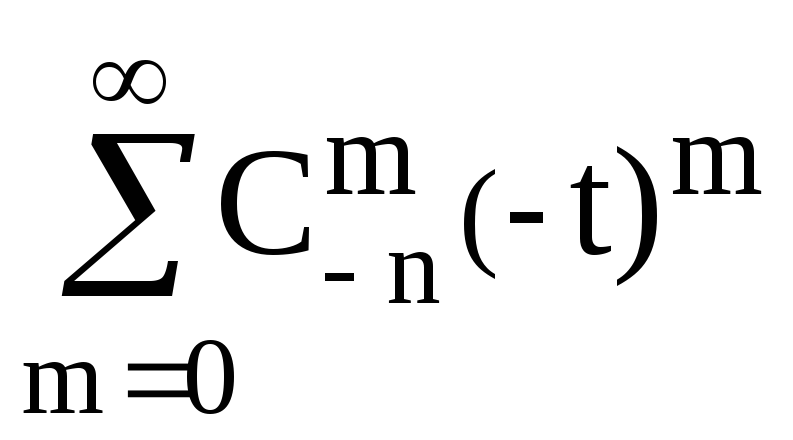Упражнение. 1. Постройте производящую функцию для сочетаний с повторениями, в которых каждый элемент входит, по крайней мере, один раз.

2. Постройте производящую функцию для сочетаний с повторениями, в которых любой элемент обязательно появляется в сочетании, но только четное число раз.

Производящие функции для перестановок.

В случае коммутативных алгебраических операций произведения х₁х₂ и х₂х₁ одинаковы. Поэтому производящую функцию, описывающую перестановки, невозможно построить так, как это было сделано для сочетаний. В случае n различных элементов из соотношения p(n,m)=”число m-перестановок” вытекает, что (1+t)ⁿ = , т. е. в разложении выражения (1+t)ⁿ число p(n,m) является коэффициентом при . Этот факт указывает пути обобщения.

Если какой-либо элемент может появляться 0,1,…,k раз или если существует k элементов данного вида, то множитель 1+t в левой части равенства заменяется множителем 1+t++…+. Это объясняется тем, что число перестановок из n элементов, p из которых одного вида, q другого и т. д., равно

.

Это число оказывается коэффициентом при в произведении

  , n=p+q+…,

что в точности соответствует необходимым требованиям.

Определение и простейшие свойства производящих функций.³

Определение. Обычной производящей функцией для последовательности a₀,a₁,… называется формальная сумма

A(t)=a₀+a₁t+a₂t²+ … a_ntⁿ+… . (1)

Экспоненциальной производящей функцией для той же последовательности называется сумма

Е(t)=a₀+a₁t+a₂t²/2!+ … a_ntⁿ/n!+… . (2)

В связи с этими определениями необходимо сделать несколько замечаний. Во-первых, элементы последовательности a₀,a₁,…, как видно, из самих обозначений, упорядочены, но не обязательно должны быть различны. Во-вторых, переменная t производящей функции никак не определена.

На производящих функциях можно определить формальные операции, такие как сложение, умножение, дифференцирование и интегрирование по t, и выявить зависимости в этой алгебре, в частности путем приравнивания коэффициентов при степенях tⁿ после выполнения этих операций. С этой точки зрения неуместно ставить вопрос о сходимости соответствующих рядов.

Алгебра степенных рядов A(t), определяющих производящие функции, известна под именем алгебры Коши, а алгебра степенных рядов E(t), определяющих экспоненциальные производящие функции, известна как символическое исчисление Блиссара. В статистике функция E(t) фигурирует как производящая функция моментов; E(t) используется также в теории чисел.

В комбинаторике неизбежно возникают производящие функции, отличные от А(t) или E(t), например, сумма вида

G(t)= a₀f₀(t)+a₁f₁(t)+a₂f₂(t)+ … a_nf_n(t)+…, (*)

для которой единственным требованием является линейная независимость функций f₀(t), f₁(t),…(для того чтобы сделать выражение однозначным). A(t) и E(t) являются частными случаями этого выражения.

Наконец, для любителей операций над непрерывными переменными следует отметить, что аналогом обычной производящей функции с одной переменной служит несобственный интеграл

А(t)=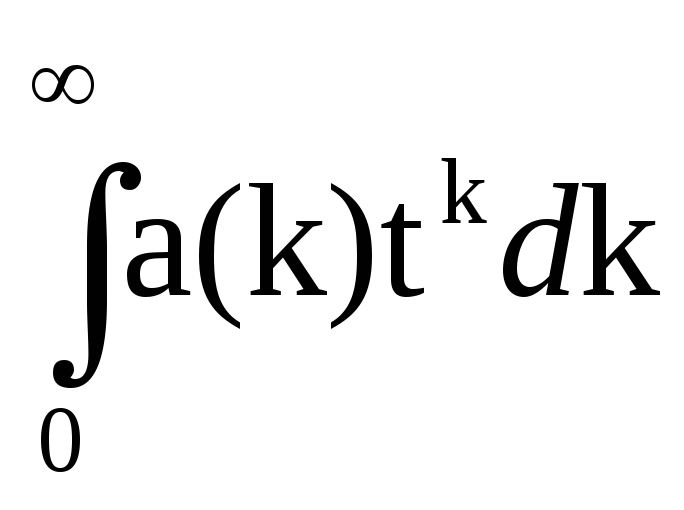

Этот факт, по-видимому, более известен для случая экспоненциального ядра е^-tk, т. е. для преобразования Лапласа

А(t)=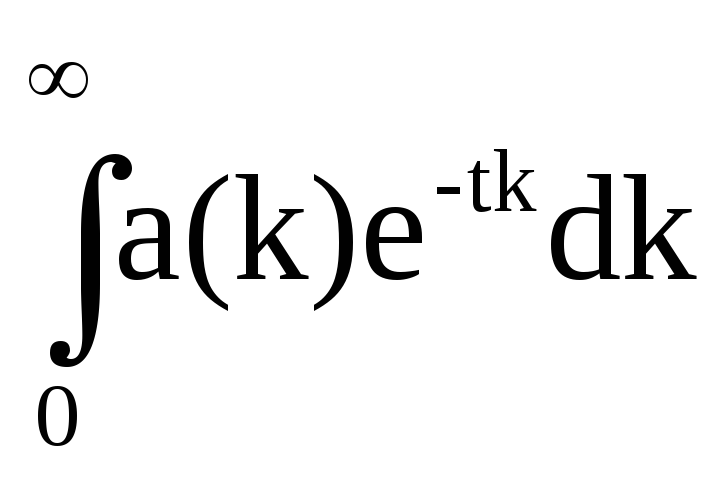

Выражение, включающее в себя как частные случаи оба приведенные выше интеграла и степенные ряды, представляет собой интеграл Стильтьеса

А(t)=,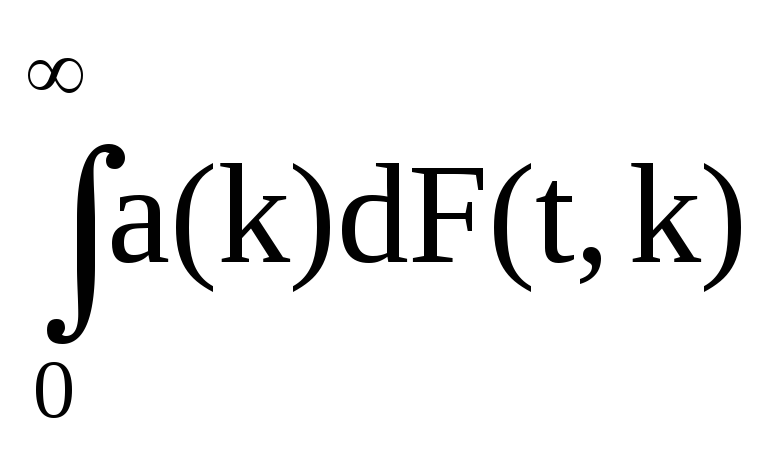

в котором t – параметр. Чтобы получить сумму (1), в качестве функции F(t,k) выбираем ступенчатую функцию. Эта функция имеет скачки при к=0,1,2,…; скачок в точке k равен t^k.

Некоторые простейшие производящие функции.

ak	A(t)	E(t)
ak	(1-at)-1	Exp at
k	t(1-t)	t exp t
k(k-1)	2t2(1-t)-3	t2 exp t
k2	t(t+1)(1-t)-3	t(t+1) exp t
c	(1+t)n	-
n(n-1)…(n-k+1)	-	(1+t)n

Упражнение. Докажите справедливость приведенных формул.

Элементарные соотношения между обычными производящими функциями.

Обозначим через A(t), B(t), C(t) производящие функции, соответствующие последовательностям (а_к), (b_к), (c_к), тогда в качестве непосредственного следствия из самого определения последовательности (а) получаем две пары соотношений; в каждой паре выполнение одного из соотношений влечет за собой выполнение второго

Сумма а_к=b_к+c_к

A(t)=B(t)+C(t)

Произведение а_к=b_кc₀+b_к-1c₁+…+b₁c_к-1+b₀c_к

A(t)=B(t)C(t)

Последовательность (а_к) называется сверткой (b_к) и (c_к), если A(t)=B(t)C(t). Сумма и произведение обладают свойствами коммутативности и ассоциативности.

Для экспоненциальных производящих функций соответствующие соотношения определяются следующим образом:

Пусть E(t), F(t), G(t) экспоненциальные производящие функции, соответствующие последовательностям (e_к), (f_к), (g_к), тогда

Сумма e_к=f_к+g_к

E(t)=F(t)+G(t)

Произведение e_к=f_кg₀+f_к-1g₁+…+f₁g_к-1+f₀g_к

E(t)=F(t)G(t)

Решение линейных рекуррентных уравнений.

Пример. Найдем производящую функцию к числам Фибоначчи: F₀=F₁=1, F_n+2=F_n+F_n+1, n0.

Производящая функция F(t) для последовательности F(0),F(1),F(2),… удовлетворяет уравнению

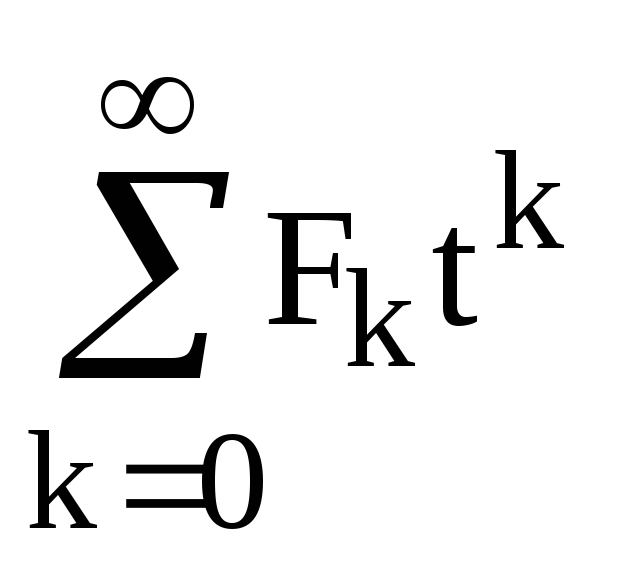F(t)==1+t+=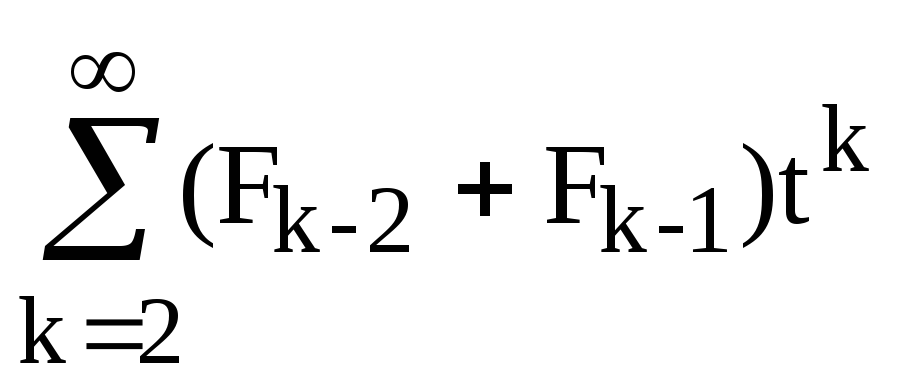

1+t+t²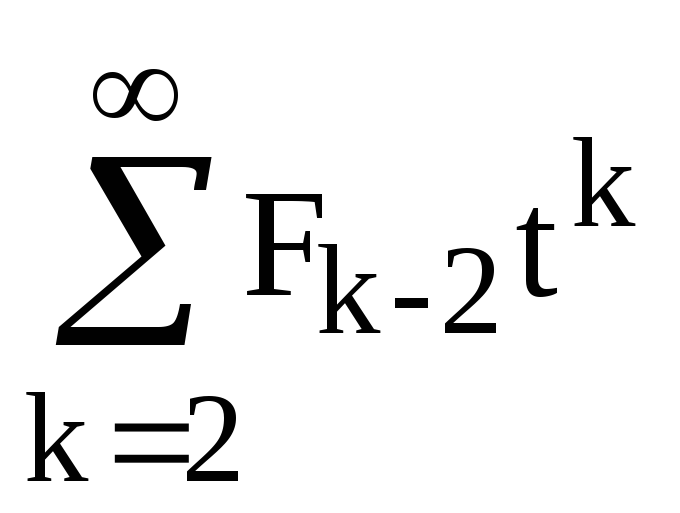+t=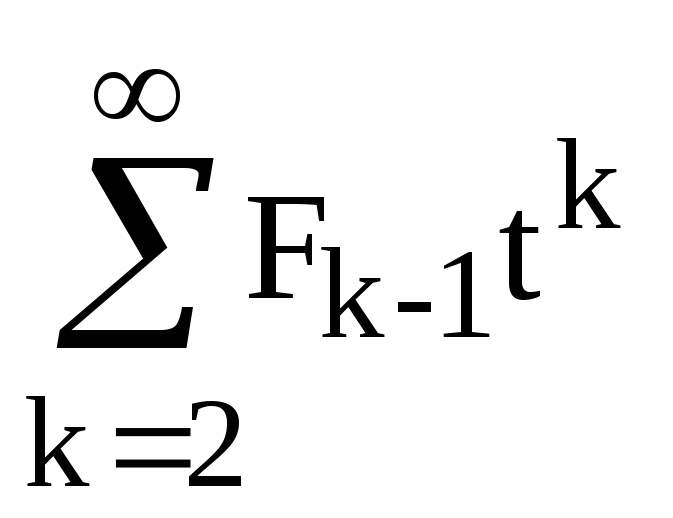

1+t+t²F(t)+x(F(t)-1)= 1+(t+t²)F(t),

т. е. F(t)=(1-t-t²)^-1.

Найдя корни уравнения 1-t-t²=0, получаем разложение

1-t-t²=(1-аt)(1-bt), где а=(1+5)/2, b==(1-5)/2.

Используя метод неопределенных коэффициентов, найдем

=+

т. е.

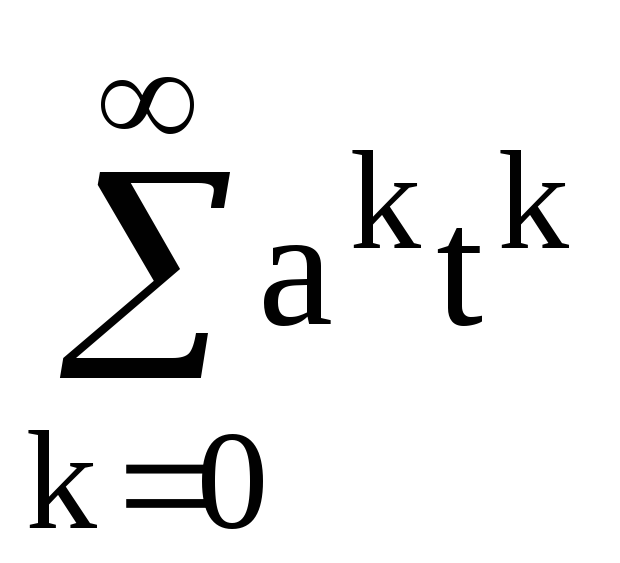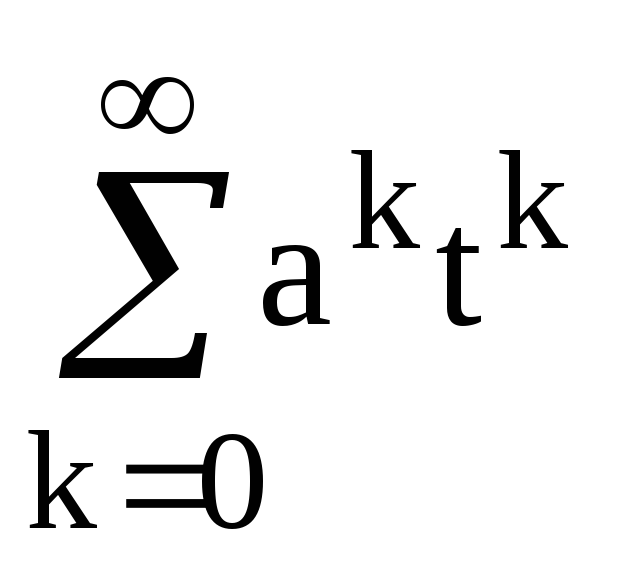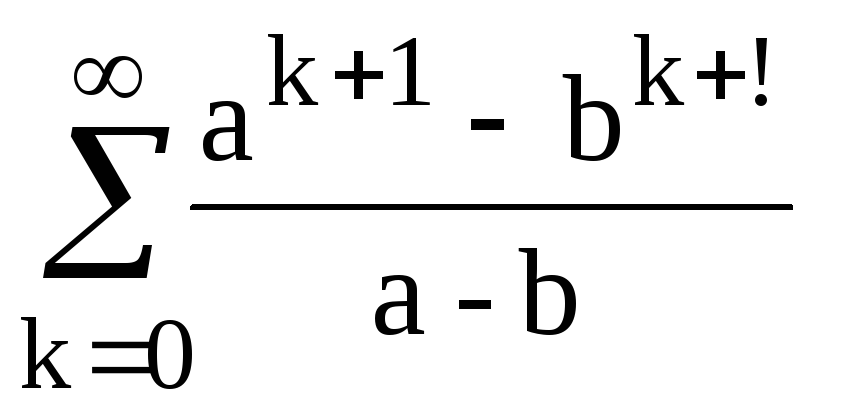F(t)=A(1-at)^-1+B(1-bt)^-1=A+B=t^k

и

F_k=+

Замечание. этот метод можно перенести на произвольное линейное уравнение с постоянными коэффициентами.

Задача 1. Пусть задана последовательность Фибоначчи

F₀=F₁=1, F_n+2=F_n+F_n+1, n0.

Рассмотрим множество последовательностей из нулей и единиц длины n, в которых нет двух рядом стоящих единиц. Пусть таких последовательностей A(n). Тогда А(n)=F_k+1.

Доказательство.

Имеем А(0)=1, так как существует только одна – пустая, такая последовательность; А(1)=2, так как существует две такие последовательности – ‘0’ и ‘1’.

Заметим, что число последовательностей длины n, у которых на n месте находится нуль, равно А(n-1).

Все последовательности длины n+1 могут быть построены из последовательностей длины n приписыванием к каждой из них на n+1 место нуля и, кроме того, тем из них, которые на n месте имеют ноль, можно также приписать единицу. Таким образом, А(n+1)=A(n)+A(n-1)=F_n+1+F_n=F_n+2.

Задача 2. n>0 А(n)==.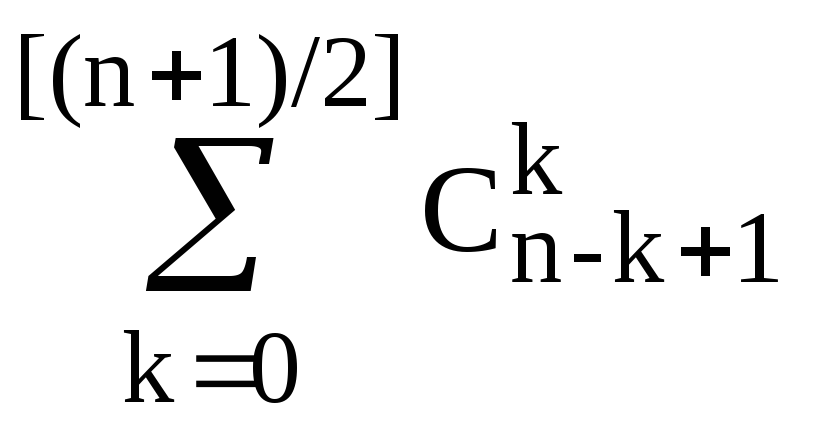

Доказательство.

А(n) можно получить следующим образом:

Заметим, что каждая такая последовательность длины n может содержать не более [(n+1)/2] единиц. Подсчитаем, сколько существует последовательностей, содержащих k единиц, 0k[(n+1)/2]. Если последовательность имеет к единиц, то она содержит n-k нулей. Рассмотрим последовательность из n-k нулей. Тогда в этой последовательности имеется n-k+1 мест для расстановки k единиц. Т. е. общее число требуемых последовательностей длины n,содержащих k единиц, равно . Таким образом, A(n)= .

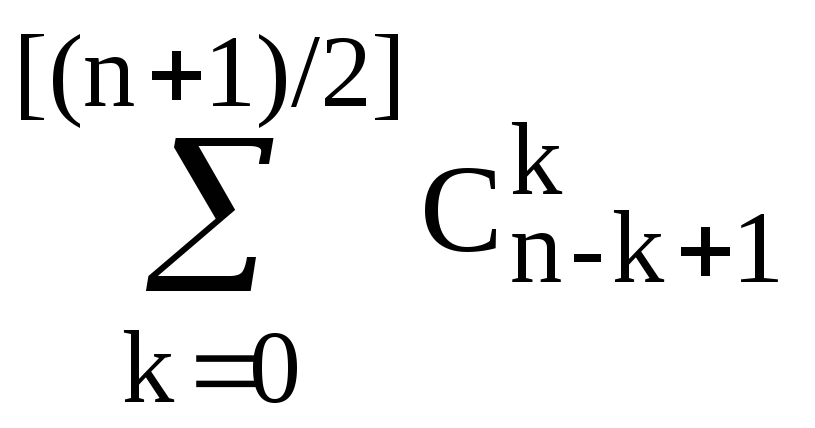Для дальнейшего анализа задач, связанных с двоичными деревьями определим их число, т. е. вычислим число неизоморфных двоичных деревьев с n вершинами.

Пусть C_n – число неизоморфных двоичных деревьев с n вершинами, тогда

C₀ = 1 - одно дерево, представленное пустым множеством вершин

C₁ = 1 

C₂ = 2  

 

C₃ = 5     

     

   

Из рекурсивного определения бинарного дерева справедливо следующее рекуррентное соотношение

C₀=1

C_n=C_k C_n-k n>0

Рассмотрим производящую C(x) = , тогда на основе определения произведения производящих функций и указанного выше рекуррентное соотношение имеем

C(x) = xC²(x)+1

или

xC²(x)-C(x) +1 = 0 {*}

Предположим, что существует функция C(x), аналитическая в окрестности нуля, удовлетворяющая этому уравнению. В силу регулярности такой функции существует ее разложение в окрестности нуля в степенной ряд (ряд Тейлора) и этот ряд удовлетворяет этому же уравнению {*}.

Для того чтобы найти необходимую аналитическую функцию, рассмотрим {*} как квадратное уравнение относительно C(x). Значение искомой аналитической функции в точке x, при x0

C(x) = {**}

Найдем разложение C(x) в степенной ряд

Разложим в ряд Маклорена

Для n>0 имеем

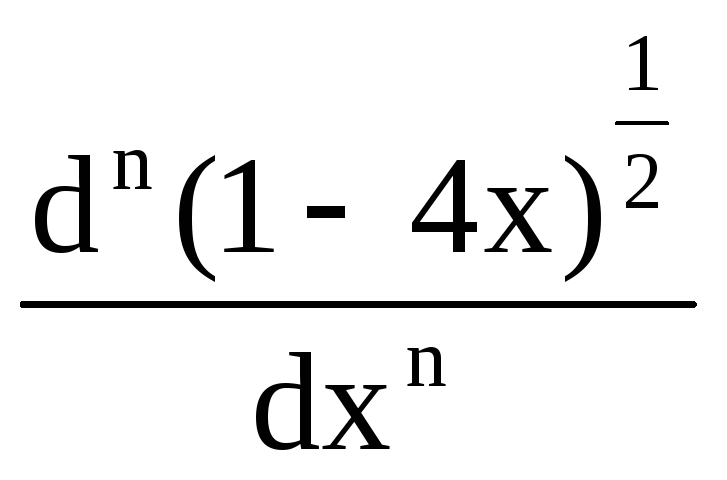= (-1)( -2)   (-n+1)(-4)ⁿ =

= 2ⁿ(-1)13    (2n-3)

и следовательно

= 1- = 1- = 1-2 =

1-

отсюда видно, что для получения решения с положительными коэффициентами следует в {**} выбрать знак минус.

Т. е.

C(x) = = = .

Отсюда окончательно получаем

C_n =

Число C_n называется числом Каталана, они часто появляются в контексте целого ряда других комбинаторных задач.

Во многих приложениях удобно представлять перестановки в циклической форме.

Рассмотрим производящую функцию С_n(t)=, определяющую число перестановок n-го порядка, имеющих k циклов, т. е. С(n,k) определяет число перестановок n-го порядка, имеющих k циклов. Тогда

C(0,0)=1,

C(n,0)=0, при n>0,

C(n,k)=0, при к>n,

Для n>0, C(n,k)=С(n-1,k-1)+(n-1)C(n-1,k) или C_n(t)=(t+n-1)C_n-1(t).

Докажем последнее утверждение.

Все ниже рассматриваемые перестановки представлены в канонической циклической форме. Заметим, что если максимальное число в такой перестановке расположено на первом месте, то оно образует отдельный цикл (так как оно является левосторонним минимумом и следующее за ним число также левосторонний минимум). Если же оно расположено на любом другом месте, то оно входит в какой-то цикл длины, большей единицы. Перестановка n-го порядка, содержащая k циклов, может быть получена либо добавлением n на первое место в перестановку (n-1)-го порядка, содержащую k-1 цикл, либо добавлением n в перестановку(n-1)-го порядка, содержащую k циклов, на любое место со второго до n-го.

Следствие. Учитывая, что C₁(t)=t, получаем

C_n(t)=t(t+1)…(t+n-1).

Числа Стирлинга первого и второго рода.

Обозначение. (t)_n=t(t-1)…(t-n+1).

Числа Стирлинга определяются следующим образом. Положим

(t)₀=t⁰=s(0,0)=S(0,0)=1

(t)_n=t(t-1)…(t-n+1)=, n>0 (1)

tⁿ=, n>0. (2)

Тогда s(n,k) и S(n,k) называются числами Стирлинга соответственно первого и второго рода. Заметим, что числа обоих рядов отличаются от нуля только для k=1,2,…,n, n>0 и что (t)_n является обычной производящей функцией для s(n,k), тогда как tⁿ является новым типом производящей функции для входящей в уравнение (*) функции f_k(t), равной (t)_k.

Упражнение. Докажите, что совокупность функций {(t)₀,(t)₁,…,(t)_n} линейно независима.

Для заданного n или k числа Стирлинга первого рода s(n,k) могут иметь тот или иной знак, действительно

(-t)_n=(-1)ⁿt(t+1)…(t+n-1),

тогда из (1) немедленно следует, что (-1)^n+ks(n,k) всегда положительно. Кроме того, учитывая вид производящей функции С_n(t), получаем С(n,k)=(-1)^n+ks(n,k). Т. е модули чисел Стирлинга первого рода s(n,k) определяют число перестановок n-го порядка с k циклами.

Рекуррентные соотношения для чисел Стирлинга первого рода s(n k) вытекают из соотношения для факториалов (t)_n=(t-n+1) (t)_n-1, т.е.

s(n,k)=s(n-1,k-1)-(n-1)s(n-1,k).

Для чисел Стирлинга второго рода, используя (2), находим

tⁿ==t=

и

S(n+1,k)= S(n,k-1)+k S(n,k). (3)

С числами Стирлинга второго рода можно связать разбиения конечных множеств, а именно:

Пусть Х={1,2,…,n}, рассмотрим всевозможные разбиения Х на k блоков. Множество таких разбиений будем обозначать П_k(X), пусть u(n,k)=|П_k(X)|, тогда

u(0,0)=1 u(n,k)=u(n-1,k-1)+ku(n-1,k). (4)

Доказательство.

Разобьем П_k(X) на два различных класса:

• тех разбиений, которые содержат одноэлементный блок {n}, и

• тех разбиений, для которых n является элементом большего (по крайней мере, двухэлементного) блока.

Мощность первого класса равна u(n-1,k-1). Т. е. такова, каково число разбиений множества {1,2,…,n-1} на k-1 блоков.

Мощность другого класса составляет ku(n-1,k), так как каждому разбиению множества {1,2,…,n-1} на k блоков соответствует в этом классе в точности k разбиений, образованных добавлением элемента n поочередно к каждому блоку.

Следствие. Сравнивая (3) и (4), получаем S(n,k)=u(n,k), т. е.

Числа Стирлинга 2-го рода S(n,k) определяют число разбиений n-элементного множества на k дизъюнктных блоков.

Теорема . Пусть |X|=n, |Y|=k, то число всех функций f:XY и f(X)=Y, равно S_n,k=k!S(n,k).

Доказательство.

Зафиксируем конкретное разбиение Х на k дизъюнктных подмножеств, тогда существует k! вариантов отображений, при которых каждому элементу разбиения сопоставляется биективно элемент Y. Каждое конкретное разбиение можно выбрать S(n,k) способами.

Принцип включения и исключения. (было у И. В. Романовского)

Пусть A₁,…,A_n некоторые подмножества (необязательно различные) конечного множества Х.

Теорема 1.(Принцип включения и исключения).

-+-…(-1)^n-1||

Доказательство

Применим математическую индукцию по n.

Для n=1 терема очевидно справедлива!

Предположим, что для произвольных A₁,…,A_n-1 выполняется

||=-+-…(-1)^n-2||

Применяя эту формулу к сумме

,

получаем

||=-+…(-1)^n-2||,

а отсюда

||==+|A_n|-||=

-+-…(-1)^n-1||.

Покажем несколько применений принципа включения и исключения

Теорема 2. Пусть |X|=n, |Y|=k, то число всех функций f:XY и f(X)=Y, равно

S_n,k=

Доказательство

Пусть У={y₁,…,y_k} и A_i={f : f:XY & y_if(X)}, тогда

f(X)Yf

Множество всех f:XY имеет мощность kⁿ. Определим 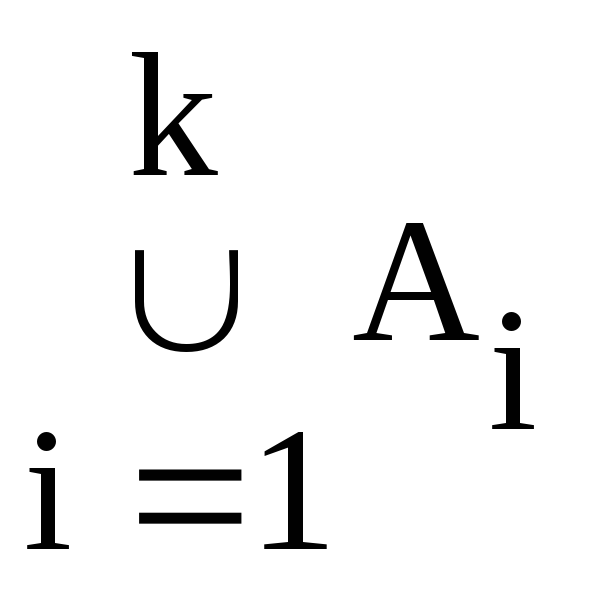, пусть 1p₁…p_ik пересечение есть множество всех функций f:XY таких, f(X), a, следовательно, мощность этого пересечения ровно (m-i)ⁿ. Согласно теоремы 1 имеем

S_n,k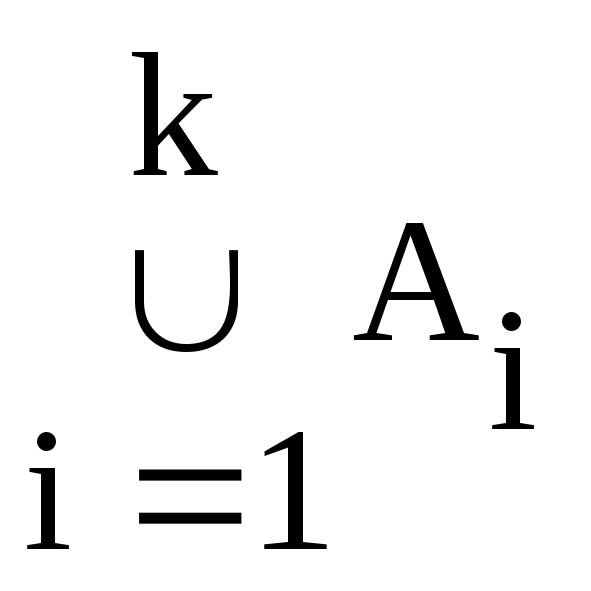=kⁿ-||=kⁿ- =

Эта формула дает простое выражение для вычисления чисел Стирлинга 2^го рода

S(n,k)= S_n,k=

Рассмотрим вопрос об определении числа “беспорядков” на множестве {1,…,n}

Определение. Под беспорядком на множестве {1,…,n} будем понимать произвольную перестановку f этого множества, такую что f(i)i для 1in.

Пусть D_n – множество всех беспорядков на {1,…,n} и

A_i={fS_n: f(i)=i}, i=1,…,n.

Заметим, что fD_n f A_i для i{1,…,n}, следовательно

|D_n|=|S_n|-+-+…(-1)^n-1||

Для произвольной последовательности 1p₁…p_in пересечение является множеством таких перестановок f, для которых f(p_j)=p_j для 1jn, и значит, ||=(n-i)!. Заметив, что последовательность 1p₁…p_in можно выбрать способами, получаем в итоге

|D_n|== =n!( )

Отметим, что сумма в скобках является начальным членом ряда е^-1=. Это означает, что беспорядки составляют е^-1=0.36788… всех перестановок.

Упражнение. Напишите программу порождения всех “беспорядков” размерности n,

 материал взят из монографии: А. Ахо, Дж. Хопкрофт, Дж. Ульман. Построение и анализ вычислительных алгоритмов. – М.; Мир,1979

 А. Ахо, Дж. Хопкрофт, Дж. Ульман. Построение и анализ вычислительных алгоритмов. – М.; Мир,1979

1 Перманенты квадратных матриц является частным случаем перманентов прямоугольных матриц. Теория перманентов рассматривается в комбинаторной математике. Она имеет приложение к решению теоретико-вероятностных, комбинаторных и физических задач [3].

2Обработка информации, хранящейся в узлах бинарного дерева, по левостороннему обходу характеризуется тем, при обработки каждой вершины вначале совершается обход левой ветви, выходящей из этой вершины; затем обработка информация хранящейся непосредственно в этой вершине; после этого, обход правой ветви, исходящей из вершины.

 материал взят из монографии: А. Ахо, Дж. Хопкрофт, Дж. Ульман. Построение и анализ вычислительных алгоритмов. – М.; Мир,1979

 Д. Кнут ‘Искусство программирования для ЭВМ’. Т 3, 5.3.3, упражнение 16.

3 Материал взят из книги Дж. Риордан ‘Введение в комбинаторный анализ’ ИЛ, М., 1962