Завдання до лабораторної роботи.

Варіант 1.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [1,2] знайти чисельний розв’язок задачі Коші: y¢=x+1+2y²; y(1)=0,5 n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 2.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [1,2] знайти чисельний розв’язок задачі Коші: y¢=1,4x–sin(x+2y²); y(1)=1,2; n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 3.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [2,3] знайти чисельний розв’язок задачі Коші: y¢=2x+cos(x²+y), y(2)=1,4, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння 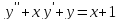з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 4.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [0,1] знайти чисельний розв’язок задачі Коші: , y(0)=0,5, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 5.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [1,2] знайти чисельний розв’язок задачі Коші: y¢=1,5y+sin(y²+0,7x), y(1)=1,6, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 6.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [0,1] знайти чисельний розв’язок задачі Коші: 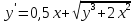, y(0)=0,4, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 7.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [0.5,1] знайти чисельний розв’язок задачі Коші: y¢=exp(–x)+0,5y², y(0,5)=2, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 8.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [0,1] знайти чисельний розв’язок задачі Коші: , y(0)=1, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 9.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [0,1] знайти чисельний розв’язок задачі Коші: , y(0)=2, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння 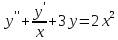з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 10.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [0,1] знайти чисельний розв’язок задачі Коші: y¢=(1–y²)cosx+0,5xy, y(0)=0, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 11.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [0,1] знайти чисельний розв’язок задачі Коші: y¢=ycos²(y–0,1x)+0,5(x²+1), y(0)=0, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

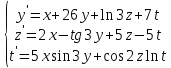що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 12.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [0,1] знайти чисельний розв’язок задачі Коші: y¢=cos(0,5+y)+x–y, y(0)=0, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 13.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [0,1] знайти чисельний розв’язок задачі Коші: y¢=exp(–1+y)+x²+y, y(0)=0, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 14.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [0,1] знайти чисельний розв’язок задачі Коші: y¢=2+0,1ysinx–0,5y², y(0)=0, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 15.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [0,1] знайти чисельний розв’язок задачі Коші: y¢=xy+ +y²+sin(2–x), y(0)=0,1, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10 знайти чисельний розв’язок системи диференціальних рівнянь

,

що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння 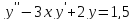з початковими умовами у(1)=0,77, y’(1)=–0,44.

Варіант 16.

1. Користуючись програмами Ейлера, удосконаленого методу Ейлера-Коші і Рунге-Кутта 4-го порядку точності, поданих вище, на відрізку [0,1] знайти чисельний розв’язок задачі Коші: y¢=xy+x²+cosy, y(0)=0,3, n=10. Користуючись перерахунком при n=20 і n=30, визначити правильні цифри наближених розв’язків.

2. Використовуючи метод Ейлера, на відрізку [0,1] при n=10

знайти чисельний розв’язок системи диференціальних рівнянь

.

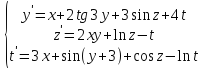що задовольняють початковим умовам: y(0)=0, z(0)=1, t(0)=1.

3. Використовуючи метод Ейлера, на відрізку [1,2] при n=10 знайти чисельний розв’язок диференціального рівняння з початковими умовами у(1)=0,77, y’(1)=–0,44.