
ЛАБОРАТОРНЕ ЗАНЯТТЯ №7
«Розв’язування диференціальних рівнянь»
Постановка задачі
Часто задачі зводяться до відшукання розв’язку певного диференціального рівняння (або системи таких рівнянь), який задовольняє певні початкові умови (задача Коші). Проінтегрувати таке рівняння в скінченому вигляді вдається досить рідко. На практиці здебільшого застосовують наближене інтегрування диференціальних рівнянь.
Задача Коші для диференціального рівняння 1-го порядку
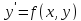 (1)
(1)
полягає у відшуканні функції y=y(x), яка задовольняє цьому рівнянню і початковій умові
y(x0)=y0, (2)
де x0, y0 – задані числа.
Задача Коші для системи диференціальних рівнянь
 (3)
(3)
полягає у відшуканні функції y1,y2,...,yn, які задовольняють даній системі і початковим умовам
y1(x0)=y10, y2(x0)=y20, ...., yn(x0)=yn0 (4)
Задача Коші для диференціального рівняння n-го порядку
y(n)=f(x, y¢, y¢¢,..., y(n–1)) (5)
полягає у відшуканні функції y=y(x), що задовольняє рівняння (5) і початковим умовам
y(x0)=y0, y¢(x0)=y10,...,y(n–1)(x0)=yn–10.
Наближені методи в залежності від форми, в якій вони подають розв’язок, можна поділити на дві групи: аналітичні методи, які дають наближений розв’язок диференціального рівняння у вигляді аналітичного виразу; чисельні методи, які дають наближений розв’язок у вигляді таблиці. Надалі припускається, що для розглядуваних рівнянь і систем рівнянь виконуються умови існування і єдності розв’язку.
Якщо відомий наближений розв’язок задачі (1)–(2) в точці хк, то проінтегрувавши рівняння (1) в межах від хк до хк+1 , знайдемо його розв’язок в точці хк+1 за формулою
 (5)
(5)
Саме ця формула є вихідною для побудови багатьох чисельних методів розв’язування задачі (1)–(2).
Метод Ейлера. Якщо інтеграл в правій частині рівності (5) обчислити за формулою лівих прямокутників, то знайдемо
у(хк+1)=у(хк)+hf(хк,у(хк))+O(h2).
Відкинувши в цій рівності доданок порядку O(h2), дістанемо розрахункову формулу
у(хк+1)=у(хк)+hf(хк,у(хк)), (k=0,1,2,..,n–1), h=хк+1–хк, (6)
яку називають формулою Ейлера.
Якщо інтеграл в правій частині рівності (5) обчислити за формулою трапецій, то знайдемо
у(хк+1)=у(хк)+h(f(хк,у(хк))+f(хк+1,у(хк+1)))+O(h3). (7)
Невідоме значення у(хк+1), що входить до правої частини цієї рівності, можна обчислити за формулою (6). Підставивши його в праву частину рівності (7), дістанемо рівність
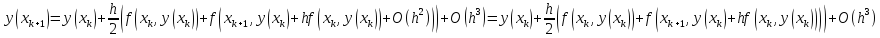
Звідси матимемо такі розрахункові формули
 ,
,
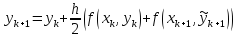 ,
,
які називають узагальненими формулами Ейлера-Коші.
Метод Ейлера легко переноситься на системи диференціальних рівнянь і на диференціальні рівняння вищих порядків. Розглянемо систему двох рівнянь першого порядку:
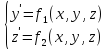
з початковими умовами y(x0)=y0, z(x0)=z0. Наближені значення y(xi)=yi i z(xi)=zi обчислюються за формулами

Для диференціального рівняння n-го порядку вводять заміну y¢=y1, y’¢=y2,...,y(n–1)=yn–1 і приходять до задачі (3)–(4), де f1=y1, f2=y2,..., fn–1=yn–1, fn(x,y1,...,yn–1,yn)=f(x,y¢,...,y(n–1),y).
Метод Рунге-Кутта. У роботі задача Коші розв’язувалась методами Ейлера. Однак вони дають порівняно великі похибки. Точнішими, хоча і громісткішими є методи Рунге-Кутта. Такі методи побудовано до 10-го порядку точності включно. В обчислювальній практиці найчастіше використовують методи Рунге-Кутта четвертого порядку точності. Алгоритм полягає у наступному.
Позначимо через h крок таблиці і побудуємо систему рівновіддалених точок xi=x0+ih (i=0,1,2...). За методом Ейлера наближене значення y(xi)=yi обчислюється послідовно за формулами:
 ,
, 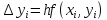 ,
i=0,1,2,
,
i=0,1,2,
За
методом Рунге-Кутта обчислення наближеного
значення yi+1
в наступній точці xi+1=xi+h
виконується за такою ж формулою як і
при методі Ейлера:
 .
Однак
.
Однак
 обчислюється
більш точно за формулою:
обчислюється
більш точно за формулою:
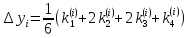
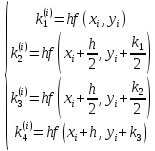
Іноді оцінити залишковий член квадратурної формули дуже важко або й неможливо, наприклад тоді, коли функцію задано таблично і аналітичний вираз її невідомий, або коли функцію задано складним аналітичним виразом і її похідні важко оцінити. Тоді використовують методи подвійного перерахунку, які передбачають двічі обчислювати означений інтеграл, але при різних h. Якщо результати практично рівні, то можна вважати, що обчислення проведено правильно і за остаточний результат взяти значення, обчислене при меншому кроці, а за похибку – різницю між одержаними значеннями.
