Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Национальный исследовательский ядерный университет «МИФИ»
Кафедра №75 «Финансовый мониторинг»
Отчёт по лабораторной работе №1
«Регрессионный анализ. Мультиколлинеарность»
Выполнила: студентка Б7-201 Хохова В.Г.
Проверила: Домашова Дженни Владимировна
Москва, 2011
Содержание
1. Постановка задачи 3
2 Оценки линейного уравнения множественной регрессии 3
3. Оценка коэффициентов классической линейной модели множественной регрессии 4
4. Анализ вариации результативного признака Y. Выборочный коэффициент детерминации 5
5. Проверка гипотезы о нормальном характере распределения регрессионных остатков 7
6. Проверка значимости уравнения регрессии и значимости коэффициентов 8
7. Проверка гипотез о значимости коэффициента ЛММР 9
8. Построение доверительных интервалов для значимых коэффициентов КЛМНР 10
9. Мультиколлинеарность 12
10. Анализ внешних признаков мультиколлинеарности 13
11. Анализ формальных признаков мультиколлинеарности 14
12. Метод пошаговой регрессии с включением переменных 16
13. Метод пошаговой регрессии с исключением переменных 17
14. Метод ридж-регрессии 18
Приложение 1 19
Приложение 2 20
Постановка задачи.
По показателям Северного, Северо-Западного, Центрального, Центрально-Черноземного, Поволжского, Северо-Кавказского, Западно-Сибирского федеральных округов провести регрессионный анализ, в качестве факторного признака выступает ожидаемая продолжительность жизни мужчин при рождении (число лет). Для этого:
1. Оценить функцию регрессии.
2. Исследовать уравнение регрессии на значимость.
3. Для значимой модели регрессии исследовать значимость коэффициентов.
4. Построить доверительные интервалы для значимых параметров связи.
5. Провести экономический анализ результатов.
Исходные данные приведены в приложении А.
Оценки линейного уравнения множественной регрессии
Не требуя
нормальный закон распределения
вектора
,
мы должны оценивать функцию
,
не обязательно линейную. Неизвестная
функция, возможно задается сложным
аналитическим выражением, но на
практике подбирают “хорошую”
аппроксимацию для
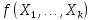из некоторого параметрического класса
функций
(β - вектор неизвестных параметров),
удобных в вычислительном плане при
оценке параметров и т.д.
Возьмем в
качестве аппроксимирующей функции
линейную функцию
или в векторной форме
где
,
Для оценки линейной функции (уравнения) множественной регрессии построим математическую модель, получим оценки коэффициентов β, изучим свойства оценок уравнения и отдельных коэффициентов.
Классическая линейная модель множественной регрессии (КЛММР)
Предположим,
что для оценки уравнения регрессии
взята выборка объемом n. Результаты
наблюдений над результативным
признаком представлены вектором
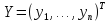и матрицей Х типа объект-свойство
наблюденных значений признаков
:
X
=
здесь
– значение j-го признака на i-м объекте
наблюдения; столбец из "1" можно
считать столбцом "наблюденных"
значений для признака
Очевидно,
что, подставляя в правую часть
наблюденные значение объясняющих
переменных для объекта наблюдение
Оi, а в левую часть наблюденное значение
результативного признака мы сможем
их уравновесить величиной
- регрессионным остатком, характеризующей
расхождение между наблюденным значением
и "осредненным" значением
- то есть значением линейной функции
регрессии:
или,
если
Система линейных уравнений называется линейной моделью множественной регрессии (ЛММР).
Отметим, что наличие регрессионных остатков в (ЛММР) объясняется вариацией результативного признака относительно "среднего значения" при данных значениях объясняющих переменных, что в свою очередь можно объяснить влиянием на результативный признак ряда неучтенных факторов-признаков.
Будем предполагать, что
1)
– детерминированные переменные;
2) ранг матрицы Х равен "к+1" – среди признаков нет линейно зависимых;
3)
- нет систематических ошибок в измерении
у;
4)
- гомоскедастичность регрессионных
остатков (равноточные измерения);
5)
- условие некоррелированных регрессионных
остатков.
Условия 4 – 5 можно заменить одним условием в векторной форме
4')
Условия (1–5) известны как условия Гаусса – Маркова. ЛММР, удовлетворяющая требованиям (1–5), называется классической ЛММР (КЛММР)
Оценка коэффициентов классической линейной модели множественной регрессии
Рассматривается линейная модель множественной регрессии:
Оценку
коэффициентов β уравнения регрессии
можно искать исходя из требований
минимума модуля отклонения наблюденных
значений
от "значений" функции регрессии,
либо из критерия минимума суммы
квадратов отклонений наблюденных
значений
от "значений" функции регрессии
(метод наименьших квадратов) более
удобного с позиции технической
реализации.
Перейдем к
оценке коэффициентов методом наименьших
квадратов (МНК). Выпишем квадратичный
функционал, обозначив через
оценку вектора β
Воспользовавшись необходимым условием существования экстремума, найдем
В силу предположения о справедливости
условий Гаусса-Маркова, в частности
(rangХ=k+1), матрица
– не вырождена и получим МНК-оценки
для вектора β :
и, следовательно, оценку
уравнения регрессии
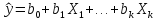
Оценим коэффициенты уравнения регрессии.
Найдем оценки основных характеристик объясняющих переменных. Результаты расчетов в пакете STATISTICA представлены на рис. 1.
Рисунок 1 – оценка математических ожиданий объясняющих переменных
Найдем оценки коэффициентов уравнения регрессии, используя пакет STATISTICA, результаты представлены на рисунке 2.
Рисунок 2 – оценка коэффициентов уравнения регрессии
Таким образом, оценка уравнения регрессии выглядит следующим образом:
Далее необходимо найти модельное значение результативного признака, вычислить оценку вектора регрессионных остатков.
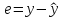
Оценка вектора регрессионных остатков представлена в приложении Б.