
- •Волго-вятская академия госслужбы
- •При президенте российской федерации
- •Институт повышения квалификации
- •И.И. Бажин
- •Н.Новгород – 2003
- •Введение
- •Часть 1. Новые принципы работы
- •Глава 1. Научные принципы менеджмента
- •1.1. Этапы развития менеджмента
- •1.2. Функции управления
- •1.3. Алгоритмы управления
- •1.4. Менеджмент как процесс принятия решений в информационной среде
- •Глава 2. Математические модели м в менеджменте
- •2.1. Типы моделей
- •2.2. Понятие о системах
- •2.3. Метод построения операционных математических моделей
- •2.4. Выбор критерия эффективности
- •2.4.1. Анализ целей
- •2.4.2. Вселенная как целеустремленная система
- •2.4.3. Требования к критерию эффективности
- •2.4.4. Свертывание критериев в многокритериальных задачах
- •2.Способ перехода к цели первого типа путем разбиения векторов на удовлетворительные и неудовлетворительные.
- •3.Метод последовательных уступок
- •2.5. Управление производством на основе моделей линейного программирования
- •2.6. Модели целочисленного линейного программирования
- •2.7. Модели сетевого планирования
- •2.8. Нелинейные модели управления
- •Матрица эффективности рекламы (долл.Прибыли/долл.Затрат)
- •Оптимальные объемы затрат на рекламу (долл.)
- •Матрица предельных значений прибыли
- •Оптимальные объемы затрат на рекламу (долл.)
- •2.9. Модели динамического программирования
2.3. Метод построения операционных математических моделей
Основной особенностью операционной методологии является поиск оптимального решения на базе математической модели и использование для ее анализа математического аппарата. Предшествующий построению математической модели всесторонний количественный анализ той или иной задачи оптимизации – неотъемлемая часть методологии исследования операций. Этот анализ осуществляется в соответствии с принципами системного подхода и предполагает, как уже отмечалось, выявление всех существенных элементов задачи и их взаимосвязей.
Степень соответствия хода операции поставленной цели характеризуется достигаемым значением функционала
W = F [x1(t), x2(t), ... , xn(t)] –
критерия оценки (показателя эффективности).
Процесс проектирования как операция имеет целью получение оптимального объекта проектирования, имеющего наилучшие возможные свойства: минимальный вес, минимальную стоимость, максимальную энерговооруженность, максимальную прибыль, минимальный срок окупаемости, минимум капиталовложений и т.п. В такой постановке создание оптимального объекта (например, системы управления производством) формализуется в виде задачи математического программирования, в которой критерий оценки отражает основную цель операции, а система ограничений обеспечивает выполнение всех требований к объекту проектирования. При этом автоматизированное проектирование оптимальных объектов и систем на основе математических методов с использованием компьютеров содержит две основные задачи:
- разработка математической модели объекта проектирования, содержащей все основные технико-экономические требования к создаваемому объекту или системе (работоспособность, технологичность, допустимая стоимость и т.п.);
- организация такого вычислительного процесса, который автоматизирует выполнение всех требований математической модели.
Схема метода построения операционных математических моделей оптимальных объектов проектирования, позволяющих на основе формализованного представления процесса проектирования как операции синтезировать оптимальные по заданному критерию параметры объекта, представлена на рис.3.3. Качественная модель проектируемого объекта, представляющая собой словесное описание требований, обеспечивающих процесс функционирования конструкции на всех этапах ее существования, формируется на основании технического задания.
Каждое из требований, записанное в виде математических выражений (для аналитических моделей), графов или матриц (для топологических моделей) или семантических правил (для семантических моделей), устанавливает основные взаимосвязи оптимизируемых параметров:
-
геометрические, позволяющие по полученным значениям искомых оптимизируемых параметров x1 , x2, x3 , ... , xn, а также по совокупности параметров а1, а2, а3, ... ,аm, заданных в качестве исходной информации, воспроизвести объект с той степенью детализации, которая необходима проектировщику при решении данной конкретной задачи;
-
энергетические, устанавливающие зависимость энергосиловых характеристик объекта от оптимизируемых параметров;
-
механические, описывающие кинематические и динамические характеристики объекта (взаимное расположение узлов и деталей конструкции в процессе ее функционирования, внешние усилия, инерционные силы, силы трения, масса конструкции и т.п.);
-
прочностные, обеспечивающие работоспособность конструкции в целом и отдельных ее узлов из условий прочности, жесткости, долговечности;
-
конструкторско-технологические, описывающие специальные конструкторские требования, а также технологические ограничения;
-
экономические, включающие в себя ограничения ресурсов проектной задачи, требования к сбыту, торговле, организационной системе.
В случае невозможности формализовать какое-либо из требований в виде математических зависимостей необходимы дополнительные теоретические и экспериментальные исследования.
Из указанных зависимостей в соответствии с основной целью проектирования формируется целевая функция
Ф = f ( x1, x2 , x3 , ... , xn; a1, a2 , a3 , ... , am )
Остальные связи параметров, записанные в виде равенств и неравенств, являются ограничениями, составляющими вместе с целевой функцией математическую модель объекта, которая на этом этапе создания должна быть подвергнута испытаниям на компьютере и, в случае необходимости, скорректирована на уровне качественной модели или математического описания. Построенная таким образом математическая модель воспроизводит образ проектируемого объекта, отвечающего всем технико-экономическим требованиям, предъявляемым в рамках данных конкретных задач проектирования, и может быть занесена в банк математических моделей системы автоматизированного проектирования.
Если полученная таким образом математическая модель состоит из линейной целевой функции, и входящие в систему ограничения равенства и (или) неравенства также линейны, то такая модель относится к классу оптимизационных задач линейного программирования, и в этом случае могут быть использованы характерные для такого класса задач методы решения (графический, симплекс-метод).
Техническое
задание
Требования
Требования Требования
Требования
к
материалам к конструкции к
сбыту к торговле
Требования
к эксплуатационным Требования
к системе
характеристикам
Математическая
модель
объекта
Критерий
оптимизации
Метод
Система
оптимизации
ограничений
Испытания
корректировка модели
Занесение
в банк
математических
моделей
Рис.3.3.
Схема метода построения математических
моделей



 Качественная
модель объекта
Качественная
модель объекта













 Теоретические
и Математическое
Теоретические
и Математическое экспериментальные
описание
экспериментальные
описание
 исследования
исследования




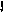



 на
компьютере
на
компьютере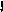

Операционная математическая модель представляет собой агрегат (совокупность) алгоритмов, описывающих функциональные свойства проектируемого объекта. Эта модель в пространстве фазовых координат, образованных гиперповерхностями входящих в модель ограничений, воспроизводит (синтезирует) образ проектируемого объекта, отвечающего всем технико-экономическим требованиям, предъявляемым в рамках данных конкретных задач проектирования.
Ситуационная задача
Пусть завод строительных материалов выпускает три вида продукции: декоративную метлахскую плитку, глазурованную облицовочную плитку и простую метлахскую плитку. Для производства этой продукции необходимы такие ресурсы, как труд рабочих, сырье и управленческий труд (труд ИТР).
Прибыль на одну тысячу штук каждого вида продукции составляет:
на 1 тыс.шт. декоративной метлахской плитки – 100 тысяч рублей, на 1 тыс.шт. глазурованной облицовочной плитки – 60 тысяч рублей, и на 1 тыс.шт. простой метлахской плитки – 40 тысяч рублей.
Затраты труда и сырьевых ресурсов на каждую тысячу единиц продукции составляют:
Затраты труда и сырья на производство 1 тыс.шт продукции
|
Вид продукции |
Затраты труда рабочих на 1 тыс.шт., часов |
Затраты сырья на 1 тыс.шт., тонн |
Затраты труда ИТР на 1 тыс.шт., часов |
|
Декоративная метлахская плитка |
1 |
1 |
2 |
|
Глазурованная облицовочная плитка |
1 |
0,40 |
2 |
|
Простая метлахская плитка |
1 |
0,50 |
6 |
Производственные мощности, структура предприятия, численность работающих таковы, что в течение рабочего дня можно использовать 100 часов труда рабочих, 60 тонн сырья и 300 часов управленческого труда.
При указанных условиях требуется определить оптимальную производственную программу предприятия.
Для построения операционной модели приведенной задачи воспользуемся методом построения такой модели, который был изложен выше.
1. Определяем оптимизируемые параметры проектной задачи. В нашем случае этими параметрами являются: X1 – ежедневное производство декоративной метлахской плитки (в тыс.шт.), X2 – количество ежедневно выпускаемой глазурованной облицовочной плитки (в тыс.шт.), X3 – объем ежедневного выпуска простой метлахской плитки ( в тыс.шт.).
2. Составляем качественную модель задачи (на основе ТЗ, которым в данном случае является условие задачи). Для этого дадим словесное описание последовательно всех основных требований нашей проектной задачи.
2.1. Численность рабочих предприятия такова, что при выпуске любых видов продукции в течение рабочего дня не может быть использовано более 100 часов труда рабочих.
2.2. Численность ИТР предприятия такова, что при выпуске любых видов продукции в течение рабочего дня не может быть использовано более 300 часов управленческого труда.
2.3. Производственные мощности предприятия таковы, что в течение рабочего дня можно использовать не более 60 тонн сырья.
Искомые параметры X1, X2, X3 (ежедневная программа выпуска плитки каждого вида) должны удовлетворять перечисленным требованиям 2.1 – 2.3 и при этих условиях обеспечить максимальную суммарную прибыль, которую в соответствии с требованиями задачи определим в качестве целевой функции (критерия эффективности) проектной задачи.
3. Опишем математически каждое из требований.
3.1.Суммарные затраты физического труда при изготовлении X1 тыс.шт. декоративной метлахской плитки, X2 тыс.шт. глазурованной облицовочной плитки и X3 тыс.шт. простой метлахской плитки не могут превышать 100 часов:
1X1 +1X2 +1X3 100 – труд рабочих (3.1)
3.2. Суммарные затраты управленческого труда при изготовлении X1 тыс.шт. декоративной метлахской плитки, X2 тыс. шт. глазурованной облицовочной плитки и X3 тыс. шт. простой метлахской плитки не могут превышать 300 часов:
2X1 + 2X2 + 6X3 300 – управление (3.2)
3.3. Суммарные затраты сырья при изготовлении X1 тыс.шт. декоративной метлахской плитки, X2 тыс.шт. глазурованной облицовочной плитки и X3 тыс.шт. простой метлахской плитки не могут превышать 60 тонн:
1X1 + 0,4X2 + 0,5X3 60 – сырье (3.3)
Целевая функция Ф, отражающая суммарную прибыль, запишется так:
Ф = 100X1 + 60X2 + 40X3
Ко всем перечисленным требованиям следует добавить требование неотрицательности всех X, так как очевидно, что объемы выпуска изделий не могут быть отрицательными числами:
X1 0, X2 0, X3 0
Таким образом, полученная математическая модель, состоящая из целевой функции Ф и системы ограничений (3.1), (3.2), (3.3) формализует нашу проектную задачу в виде задачи математического программирования:
максимизировать целевую функцию прибыли
Ф = 100X1 + 60X2 + 40X3 max
при ограничениях
X1 + X2 + X3 100
2X1 + 2X2 + 6X3 300
X1 + 0,4X2 + 0,5X3 60
X1 0 , X2 0 , X3 0
Решение этой формализованной задачи с помощью компьютера дает следующие оптимальные параметры производственной программы:
X1 = 33,33 тыс.шт.; X2 = 66,67 тыс.шт.; X3 = 0;
При этом максимальная ежедневная прибыль предприятия составляет
Ф = 7333,3 тыс.руб.
Полученное оптимальное решение предусматривает производство только декоративной (33 330 шт. в сутки) и глазурованной метлахской плитки (66 670 шт. в сутки). То есть производство простой метлахской плитки в этих условиях для предприятия невыгодно.
Здесь следует отметить, что само условие задачи (т.е. наше техническое задание) исходило лишь из возможностей и выгод предприятия и никак не учитывало общественные потребности в виде минимально необходимого количества продукции того или иного вида. Если бы это учитывалось, то в модель в качестве ограничений эти условия были бы добавлены. Например, в условии содержалось бы требование: завод должен удовлетворить ежедневную потребность в простой метлахской плитке в количестве не менее 5000 шт. Тогда соответствующее ограничение выглядело бы так:
X3 5
Это ограничение добавилось бы к модели и, естественно, изменило бы оптимальное решение. При этих новых условиях и величина максимально возможной прибыли изменилась бы (в данном случае, очевидно, уменьшилась бы).
Важное достоинство моделей, построенных по рассмотренному нами методу, заключается в том, что они остаются открытыми, и при изменении постановки задачи проектирования могут дополняться новыми ограничениями. Возможно также и построение усеченных моделей, учитывающих по желанию проектировщика не все требования исходной задачи.
В соответствии с рассмотренным методом построения операционных (синтезирующих) моделей объектов проектирования отличительным качеством является обязательный в процессе их создания этап испытания на компьютере, что дает возможность наглядно выявить все несоответствия и неточности (в постановке задачи, формировании критерия эффективности или системы ограничений). Эти несоответствия проявляются в синтезе по такой модели несообразных конструктивных параметров объекта (синтез конструктивного «урода»). На этапе корректировки модели такие неточности эффективно устраняются.
В рассмотренном примере синтезированный результат X3 = 0 мог бы в принципе рассматриваться как несообразный (уродливый): ведь предприятие имеет соответствующее оборудование для выпуска простой метлахской плитки, да и потребность в этой плитке имеется. Тогда, посчитав такой результат (X3 = = 0) нелепым, мы бы обратились к качественной модели и обнаружили бы, что не учли общественные потребности в этом виде продукции, и дополнили бы модель соответствующим ограничением, о котором говорили ранее: X3 5.
Если же такое дополнение не предусматривалось техническим заданием на задачу, то следовало бы проверить правильность исходной информации (количество труда и сырья на производство единицы продукции, а также величину удельной прибыли).
Поскольку полученный результат X3 = 0, по сути, превращает наш проект в задачу с двумя переменными, рассмотрим ее решение графическим методом, который позволяет довольно просто решать линейные задачи математического программирования.
Определение. Если операционная математическая модель состоит из линейной целевой функции, и входящие в систему ограничений равенства и (или) неравенства также линейны, то такая модель (и соответствующая проектная задача) относится к классу оптимизационных задач линейного программирования, и в этом случае могут быть использованы характерные для такого класса задач методы решения (графический, симплекс-метод).
Таким образом, в сформулированной нами задаче линейного программирования (для двух переменных X1 и X2, при X3 = 0) требуется найти значения переменных X1 и X2, удовлетворяющие всем ограничениям и обеспечивающие максимальное значение целевой функции.
Для двух переменных наша задача примет вид (подставим X3 = 0 во все выражения полученной ранее модели)
X1 + X2 100
2X1 + 2X2 300
X1 + 0,4X2 60
X1 0 , X2 0
Пусть, например, координаты точки X1 = X10, X2 = X20 таковы, что для этой точки выполняются все ограничения. Такая точка называется допустимым решением. Множество допустимых решений называется допустимой областью. Решение задачи линейного программирования состоит в отыскании наилучшего решения в допустимой области. Лучшее допустимое решение задачи называется оптимальным. Значение целевой функции, соответствующее оптимальному решению, называется оптимальным значением задачи математического программирования.
При использовании графического метода решения для изображения допустимой области следует начертить графики всех ограничений (прямые линии). Каждая прямая разделяет область на две полуплоскости (допустимую и недопустимую). Пересечение допустимых полуплоскостей определяет многоугольник, который и представляет собой множество допустимых решений задачи (допустимую область). Эта область, образованная ограничениями g1(x1,x2) – g3(x1,x2), на рис.3.4 показана заштрихованным треугольником.
Если зафиксировать значение целевой функции Z = C1X1 + C2X2, то соответствующая этому значению точка будет лежать на некоторой прямой. При изменении величины Z эта прямая подвергается параллельному переносу. Пусть C1 и C2 таковы, что при удалении прямой от начала координат значение целевой функции увеличивается. Двигая прямую вверх параллельно самой себе, приходим к такому положению Zmax, когда прямая и допустимое множество будут иметь только одну общую точку А. Очевидно, что точка А с координатами X1 = X1 и X2 = X2 и есть оптимальное решение, так как она лежит на прямой с максимально возможным значением Zmax. Пользуясь изложенным методом, решим графически нашу задачу.
Преобразуем систему ограничений к виду
X1 /100 + X2 /100 1
X1 /150 + X2 /150 1
X1 /60 + X2 /150 1
X1 0 , X2 0 ,
а целевую функцию запишем в виде
100X1 /Ф + 60X2 /Ф = 1
Пусть Ф(1) = 100x60. Тогда для этого фиксированного значения Ф(1) уравнение прямой имеет вид
X1 / 60 + X2 / 100 = 1
Рис.3.5
Прямая, соответствующая полученному выражению, представлена на рис.3.5 штрих-пунктирной линией. Здесь же изображены прямые, соответствующие системе ограничений: (1) – труд рабочих; (2) – управление; (3) – сырье. Жирными линиями выделена допустимая область, очерченная прямыми, соответствующими ограничениям по труду рабочих и сырью, а также осями абсцисс и ординат, что соответствует требованию неотрицательности оптимизируемых параметров. Оптимальным решением является точка А, лежащая на пересечении двух ограничений – (1) и (3).
