2.6. Модели целочисленного линейного программирования

Рассмотренные ранее модели линейного программирования предполагали, что управляющие переменные – объемы выпуска продукции – представляют собой непрерывные параметры. Вместе с тем, существует большое число задач управления, в которых управляющие переменные по самому смыслу решаемой проблемы могут быть только целыми числами. Примерами могут служить задачи, связанные с определением численности трудовых ресурсов (число работающих должно выражаться целым числом), решение задач об оптимальном распределении единиц подвижного состава на транспортных маршрутах города (на маршруте не может находиться, скажем, 3,5 трамвая), оптимизация распределения станочного парка между цехами предприятия и т.п. Такого рода задачи должны формулироваться как задачи целочисленного программирования. Следует заметить, что зачастую такого рода задачи на практике решают как обычные, с непрерывными параметрами, поскольку используемые методы оптимизации в таком случае гораздо более просты. Однако, несмотря на эффективность такого подхода, в ряде ситуаций он может привести к существенным ошибкам, поскольку полученное таким способом решение может даже оказаться недопустимым.

Рассмотрим модель оптимизации (3.13) из раздела 3.5

c₁x₁ + c₂x₂ + c₃x₃ + . . . + c_nx_n  max

a₁₁x₁ +a₁₂x₂ + a₁₃x₃ + . . . + a_1nx_n  b₁

a₂₁x₁ +a₂₂x₂ + a₂₃x₃ + . . . + a_2nx_n  b₂ (3.19)

a₃₁x₁ +a₃₂x₂ + a₃₃x₃ + . . . + a_3nx_n  b₃

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a_m1x₁ +a_m2x₂ + a_m3x₃ + . . . + a_mnx_n  b_m

x_j  0 (j = 1,n)

Если наряду с ограничениями задачи (3.19) потребовать, чтобы все переменные x_j (j = 1,n) были целыми, то задача становится задачей целочисленного линейного программирования.

Ограничения задачи (3.19) определяют в n-мерном пространстве выпуклую область OABCD. На рис.3.6 эта область изображена в плоскости двух координат – X_k и X_i. Узлы целочисленной решетки показаны точками. Такие точки, расположенные внутри области OABCD, являются допустимыми решениями задачи целочисленного программирования. Как было показано ранее, оптимальные решения задачи линейного программирования всегда располагаются на границе допустимой области. В данном случае граничные точки не являются даже допустимыми решениями, поскольку ни одна из них не целочисленна. Предположим, что допустимая область сужена до выпуклого многогранника допустимых целочисленных точек внутри допустимой области. На рис.3.6 часть этого выпуклого многогранника изображена в плоскости переменных X_k, X_i в виде заштрихованной области OEFGH, которую можно рассматривать как область допустимых решений некоторой другой задачи линейного программирования. Действительно, если к задаче линейного программирования, определяющей допустимую область OABCD, добавить ограничения типа RR₁, как показано на рис.3.6, то для вновь полученной задачи многоугольник OEFGH будет областью допустимых решений.

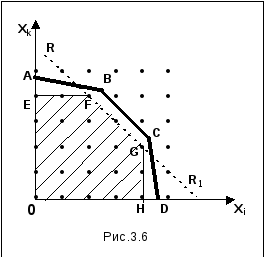
Эта область обладает двумя важными свойствами: 1) содержит все допустимые целочисленные точки исходной задачи линейного программирования (поскольку является выпуклым многогранником этих точек); 2) все крайние точки новой области целочисленны. Поэтому любое базисное решение модифицированной задачи линейного программирования имеет своими компонентами целые числа и является искомым оптимальным решением задачи целочисленного линейного программирования.

Как только будут введены упомянутые выше дополнительные ограничения, обеспечивающие выполнение указанных условий 1) и 2), можно решить модифицированную задачу линейного программирования любым обычным методом, и полученное решение автоматически будет целочисленным.

Рассмотрим в качестве примера следующую задачу.

Для приобретения оборудования по изготовлению комбикормов фирма может выделить 36 тыс.руб. Оборудование должно быть размещено на производственных площадях, не превышающих 60 кв.м. Фирма может заказать оборудование двух видов: менее мощные машины типа A стоимостью 3 тыс.руб., каждая из которых требует для размещения производственную площадь 3 кв.м. и обеспечивает производительность за смену 2 т комбикормов, и более мощные машины B стоимостью 4 тыс.руб., каждая из которых занимает площадь 5 кв.м. и обеспечивает производительность 2,7 т кормов за смену.

Требуется составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что фирма может приобрести не более 8 машин типа B.

Решение. В качестве управляющих переменных данного бизнес-проекта выбираем: x₁ – количество приобретаемых машин типа A и x₂ – количество приобретаемых машин типа B. Тогда, определив целевую функцию Z, выражающую суммарную производительность, которую требуется максимизировать, получим математическую модель задачи в виде

Z = 2x₁ + 2,7x₂  max (3.20)

при ограничениях

3x₁ + 5x₂  60 (1)

3x₁ + 4x₂  36 (2)

x₂  8 (3) (3.21)

x₁  0, x₂  0

x₁, x₂ – целые числа (3.22)

Решим эту задачу графически (рис.3.7). Здесь OKLM – область допустимых решений задачи (3.21), ограниченная прямыми (1), (2), (3) и осями координат. Точками представлена сетка целочисленных значений параметров. Точка L с координатами (4/3, 8) – это точка оптимального, но не являющегося целочисленным, решения задачи (3.21). Прямая (4) является прямой, отсекающей два целочисленных решения, лежащих в допустимой области. При добавлении в систему ограничений условия, соответствующего прямой (4), получим допустимую область расширенной задачи. Эта область на рис.3.7 представлена многоугольником OKNM. В данном случае отсеченное прямой (4) целочисленное решение – точка N(4,6) и является оптимальным решением целочисленной задачи. Таким образом, решение поставленной задачи: Z* = 24,2 при x₁* = 4, x₂* = 6, то есть максимальную производительность 24,2 тонн комбикорма за смену можно достичь приобретением 4 машин малой производительности и 6 машин большой производительности. При этом, поскольку ограничение (1) оказалось неактивным, останется незанятой часть помещения площадью 60 – (12 + 30) = 18 кв.м.

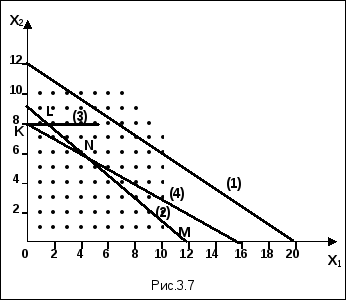
Следует заметить, что если использовать оптимальное решение нецелочисленной задачи – (4/3, 8) и округлить (как это часто делается на практике) до ближайшей допустимой точки, то мы получили бы x₁* =1, x₂ =8. При этих значениях x величина производительности Z = 23,6, что, как видим, не является лучшим решением.