21.Арифметические свойства пределов

1.теорема о пределе произведения

предел произведения конечного числа функций, каждая из которых имеет конечный предел в т. _х0, существует и равен произведению предельных множителей

2.сумма конечного числа функций, каждая из которых имеет конечный предел, также имеет пределы равные сумме пределов их слагаемых.

3.предел частного двух функций, каждая из которых имеет конечный предел, равен частному двух пределов, если предел знаменателя в т. х₀ не равен 0

При вычитании пределов могут возникнуть неопределенности вида

В случае неопределенности принимают либо разложение числителя или знаменателя на множители, либо умножение на выражение сопряженное иррациональности и применяют формулу разности квадрата.

При раскрытии неопределенности в числителе и знаменателе выносят за скобки старшую степень и производят сокращение.

Вычисляют пределы также с помощью замечательных пределов.

22.Теорема о единственности предела функции

Функция в точке не может иметь более 1 предела

Дано:

Доказать: предел единственен

Доказательство: предположим, что в т. х₀ существует еще один предел функции равной В

А≠В это значит, что можно указать окрестности т. А, В, которые не пересекаются

Тогда это значение х будет є и 1окрестность и 2, но тогда соответствует значение функции попадает в и функция є , а это значит что пересечение окрестностей т. А, В не пустое множество, пришли к противоречию, значит предположение сделано неверно.

23.Теорема о пределе промежуточной функции

(о двух милиционерах)

Пусть даны 3 функции:

Доказать:

Доказательство:

По условию - (1)

-(2)

-(3)

Выберем наименьшую из окрестностей:

Выберем произвольное х окрестности т. х₀ нового радиуса

Получили:

Теорему иногда шутливо называют «принципом двух милиционеров». Роль «милиционеров» играют функции φ(х) и g(х), функция ƒ(х) «следует за милиционерами»

24. Теорема о предельном переходе в равенстве, в неравенствах

Равенство

Если в некоторой окрестности т. _х0 для х≠ х₀ и достаточно близких к т. _х0 функции f₁=f₂ и в т. х₀ существуют пределы этих функций, то эти пределы также равны

Доказать: А₁=А₂

Обратная теорема верна не всегда, различные функции могут иметь в некоторой точке равные пределы, но во всех остальных точках взятых из окрестностей точки их значения различны.

_А1=_А2

Неравенство

1. Если функции _f1, _f2 в т. х₀ имеют пределы _А1<_А2, то существует окрестность в т. х₀, такая что для любого х этой окрестности

1.если предел функции в т., то для любого , так что функция

2.

2. Если для и выполняется неравенство и существует предел

Доказать:

Неравенство между функциями либо сохраняется, либо переходит в неравенство

1.

2.

25. Непрерывность функции в точке

Пусть дана функция -предельная т.Х,

-значение функции в т._х0

1. функция называется непрерывной в т.

Это определение предъявляет к функции следующие требования

1.функция определена в т. _х0 и ее окрестности

2.существует конечный предел функции в т._х0

3.предел функции совпадает с ее значением в т._х0

2.f- не проходит в т.

3. обозначим ,

,

f- непрерывна в т.

4. f – называется непрерывной в т.,

Доказать: что функция в т. _х0 не является непрерывной

хотя т.0 не принадлежит множеству Х, любая ее окрестность, содержащая бесконечно много точек из области определения отличных от _х0

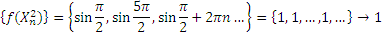
Нашлись 2 различные последовательности значений переменных х стремящихся к 0 такие, что соответствующие последовательности значений функций стремятся к различным числам - это значит, что в т.0 предела не имеет функция не является не прерывной т.к. нарушено 2 требование непрерывности. Более того в т. _х0=0 нарушена и 1 требование непрерывности, функция в т.0 неопределенна.

Профункцией которой в т. _х0 не является непрерывной говорят что они в этой точке терпят разрыв