10.Предел числовой последовательности ее геометрический смысл

Если ЧП рассмотреть как функцию, заданную на множестве натуральных чисел и использовать определение конечного предела функции на бесконечности, то получим следующее определение ЧП:

lim_n_=A(>0)(n_N)(nN:n> n_)Ix_n-AI<

Геометрический смысл: это значит, что в любой окрестности точки А под  будут находиться все члены последовательности x_n, начиная с некоторого номера. Вне этой окрестности может находиться лишь несколько первых членов числовой последовательности, их количество n_. Число n_ зависит от .

Определение предела не дает способа его отыскания, но позволяет установить является данное число пределом последовательности или нет.

См.примеры в тетради…

11.Теорема об ограниченности сходящейся числовой последовательности

Ч.П. называют сходящейся, если она имеет конечный предел при n->. Если ч.п. предела не имеет, или он бесконечен, то она называется расходящейся.

Теорема : Если ч.п. сходится, то она ограничена.

Дано: 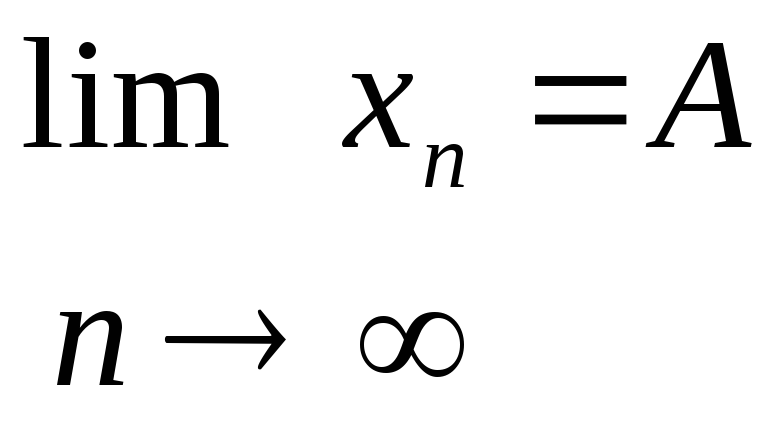где А – число.

Доказать: {x_n} - ограничена.

Доказательство:

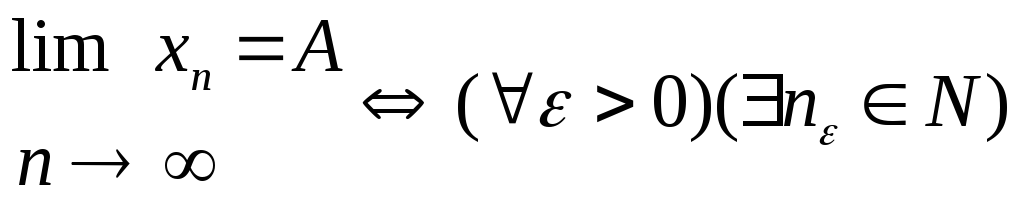
А-=m₁

А-=M₁

m₁ < x_n< M₁

Последнее неравенство означает, что все члены последовательности, начиная с некоторого номера, находятся на промежутке (m₁;M₁). За пределами этого интервала находится лишь несколько первых членов последовательности, на числовой прямой они занимают фиксированное положение, а это значит, что границы интервала можно раздвинуть так, что все члены последовательности, начиная с первого номера, попадают внутрь нового промежутка (m;M), а это значит, что {x_n} – ограничена.

12.Понятие под последовательности Теорема Больцано-Вейерштрасса.

Пусть - монотонно возрастающая последовательность натуральных чисел, тогда последовательность называется подпоследовательностью последовательности. Теорема Вейерштрасса: из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Доказательство: пусть а_n - ограничена. Это значит, что .

Множество значений последовательности является множеством ограниченным. Если множество значений последовательности конечно, то из данной последовательности можно выделить стационарную подпоследовательность (предположим противное: пусть стационарной последовательности не существует, тогда множество значений последовательности бесконечно – противоречие!!!!). В этом случае теорема доказана, так как любая стационарная последовательность сходится.

Если множество значений бесконечно, тогда оно представляет собой бесконечное подмножество множества действительных чисел и, в силу принципа Вейерштрасса, имеет хотя бы одну предельную точку. (Дополнительное определение - принцип Вейерштрасса - любое бесконечное ограниченное множество точек на числовой прямой имеет хотя бы одну предельную точку. Точка x₀ называется предельной точкой для множества, если любой интервал, содержащий точку x₀, содержит бесконечное число точек из этого множества).

Обозначим эту предельную точку через α и покажем, что в последовательности α_n существует подпоследовательность, сходящаяся к α.

Действительно, так как α - предельная точка для множества значений α_n последовательности, то в любой ε окрестности точки α найдется бесконечное число членов последовательности α_n .

Примеры:

Пусть ε=1. Тогда

Пусть ε =. Рассмотрим окрестность . Так как в любой окрестности точки α находится бесконечно много членов последовательности α_n , то найдется член последовательности α_n с номером, большим чем n₁: .