Приклад

Коли судно швартується, матрос накладає канат вісімкою на 2 чавунних стовпа (2 кнехта). Натяг канату дорівнює , сила, з якою матрос тримає канат у рівновазі, дорівнює . Кут охоплення канатом кожного стовпа дорівнює 210⁰. Коефіцієнт тертя каната по чавунному стовбу дорівнює μ = 0,15.

Визначити натяг канату, який матрос може утримати силою F = 600 Н.

Д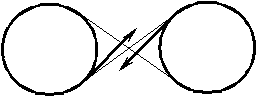ано:

F = 600 Н;

α = 210⁰;

μ = 0,15.

Q =?

Рис. 20

Кут охоплення канатом одного стовпа дорівнює

.

При накладенні трьох вісімок кут охоплення канатом стовбів буде у шість разів більше, тобто 7π.

Тоді залежність натягів двох кінців каната визначається за формулою Ейлера.

.

Логарифмуючи, знаходимо шуканий коефіцієнт тертя між канатом та чавунним стовбом:

,

звідки маємо:

.

Отже. При відомих значеннях μ і F маємо:

і Q = 27600 =16200 Н.

Відповідь: Q =16200 Н.

Кінематика Кінематика точки

а) Рівнозмінний рух точки по прямій

1. Точка, рухаючись прямолінійно, пройшла шлях Ѕ = 200 м протягом 10 с, маючи прискорення 0,01 м/с². Визначити швидкості точки: початкову, кінцеву, середню.

Відп: ν₀=15 м/с; ν_к=25 м/с; ν_ср=20 м/с.

2. Санки спускаються з гори прямолінійно без початкової швидкості і проходять за 0,5 хв. шлях 200 м. Визначити прискорення санок, вважаючи його сталим, і швидкість у кінці шляху.

Відп.: а = 0,44 м/с² ; ν =13,33 м/с.

б) Довільний рух точки

3. Судно рухається прямолінійно відповідно до рівняння: s = 4t³ м. Знайти середню швидкість і середнє прискорення судна за час від t₁ = 1 с до t₂ = 3 с.

Відп.: ν_ср = 52 м/с ; а_ср= 48 м/с².

4. Задано рівняння руху точки: х = 20 cos² t; y = 30 sin² t, де x, y – в м; t – в с.

Визначити рівняння траєкторії точки, її швидкість і прискорення в момент часу t = π/2 с.

Відп.: х/20 + у/30 =1; ν = 0; а =72,1 м/с².

5. Точка рухається відповідно до рівнянь: х = 3 t²;

у = 6 t; де x, y – в м; t – в с.

Знайти швидкість і прискорення точки.

Відп.: ν = 6+ t² м/с; а = 6 м/с²; cos (ν,x) = t/+t² ; cos (ν,x) =1/+ t²;

cos(a,x)=1; cos(a,y)=0.

6. Судно рухається згідно з рівнянням:

.

Визначити величину початкової швидкості судна.

Відп.:.

Приклад 1

Визначити відстань і пройдений шлях для моменту часу Т = 5 с, якщо точка М рухається з постійною швидкістю v = 80 см/с по колу, заданому рівнянням (х, y — у см)

х² + y² = 2500,

у напрямку ходу годинникової стрілки. Початок відліку відстаней у точці А(50;0). Початкове положення точки М₀ (—50; 0).

Розв’язання

Траєкторія руху точки – крива лінія (коло). Рух точки по цій траєкторії з постійною швидкістю описується рівнянням:

s = s₀ +V₀t.

Відлік відстаней починається в точці А, а рух починається з точки М₀, отже:

s₀=АМ₀ = πR = 3, 1450 = 157 см.

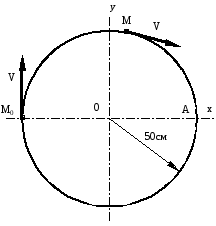
і рівняння руху в цьому випадку прийме вигляд:

s = 157 + 80t (s — у см, t — у с).

За 5 с руху точка пройде шлях:

805 = 400 см,

і виявиться в положенні М на відстані:

s = 157 + 400 — 2πR = 557 — 314 = 243 см,

від точки А, причому спочатку ця відстань збільшується від 157 до 314 см (точка М підійшла до А з іншої сторони), потім, при другому обході, від 0 до 557 — 314 = 243 см (дуга АМ_оМ на рис.).

Важливо помітити, що при розглянутому криволінійному русі точки модуль швидкості не змінюється, а напрямок вектора швидкості змінюється.

Відповідь: s =243 см.