- •Одесская национальная академия пищевых технологий
- •Конспект лекций
- •Глава 1. Основные понятия информатики и компьютерной техники.
- •1.1. Информация и информатика
- •1. 2. Устройства, характеристики и программное обеспечение пк
- •Основные характеристики современных пк
- •Программное обеспечение пк
- •3. Файловая система организация данных
- •Project.Vbp - проект Visual Basic;
- •1.4. Операционная система Windows
- •1.5. Пользовательский графический интерфейс
- •Окна в Windows
- •Глава 2. Обзор ресурсов и управление в Windows
- •2.1. Главное меню рабочего стола и справочная система
- •Справочная система Windows
- •2.2. Программа Проводник для работы с папками и файлами
- •2.3. Работа с папками в окне Проводник
- •2.4. Работа с файлами в окне Проводник
- •Глава 3. Текстовой редактор Word.
- •3.1. Создание и сохранение документа.
- •Ввод текста
- •Выделение текста
- •Отступы, выравнивание и межстрочные интервалы
- •Установка гарнитуры и размера шрифтов
- •Ввод символов
- •3.3. Редактирование текста страницы
- •Удаление, копирование, перемещение и вставка текста
- •Вставка текста из другого документа
- •3.4. Колонки и таблицы в Word Расположение текста колонками
- •Создание таблицы
- •Глава 4. Формульный редактор и графика в Word
- •4.1 Формульный редактор
- •Создание гиперссылки
- •Графика в Word Графические объекты - рисунки, фотографии, диаграммы и пр. В документах Word часто используется различного вида графика:
- •4.2. Работа с рисунками
- •Меню вставки рисунка
- •Глава 5. Табличный процессор ms Excel
- •5.1. Рабочие книги, листы и окно Excel
- •5.2. Некоторые операции над рабочей книгой и листами
- •Операции над рабочим листом
- •Выделение элементов листа
- •Работа с ячейками
- •5.3. Типы данных в Excel и их ввод
- •5.4. Арифметические и логические выражения в Excel
- •Глава 6. Вычисления в Excel
- •6.1. Абсолютные, относительные и смешанные адреса
- •6.2. Стандартные функции
- •Мастер функций
- •6.3. Логические функции если в Excel
- •Пример применения функции если
- •6.4. Функции обработки текстовых данных: Функции найти и поиск
- •Функции правсимв и левсимв
- •Функции сжпробелы и печсимв
- •Функция пстр
- •Функции заменить и подставить
- •Функция повтор
- •Функция сцепить
- •Функция текст
- •Функция рубль
- •Функция длстр
- •Функция совпад
- •Функции прописн, строчн и пропнач
- •Функция значен Функция значен преобразует строку текста, отображающую число, в число. Синтаксис:
- •6.5. Работа с датами Как вводить даты и время в Excel
- •Быстрый ввод дат и времени
- •Как Excel хранит и обрабатывает даты и время
- •Количество дней между двумя датами
- •Количество рабочих дней между двумя датами
- •Сдвиг даты на заданное количество дней
- •Сдвиг даты на заданное количество рабочих дней
- •Вычисление дня недели
- •Как посчитать сколько дней в месяце
- •Глава 7. Диаграммы в Excel и решение прикладных задач
- •7.1. Мастер диаграмм
- •7.2. Построение диаграммы типа Поверхность
- •7.3. Редактирование построенной диаграммы
- •7.4. Решение нелинейных уравнений в Excel
- •7.5. Вычисления по итерационным формулам
- •Глава 8. Обработка статистических данных в Excel
- •8.1. Некоторые понятия математической статистики
- •8.2. Генерация случайных чисел и построение гистограмм
- •Построение гистограмм
- •8.3. Описательная статистика
- •Глава 9. Работа с базами данных в Excel
- •9.1. Основные понятия и правила создания бд
- •Номер первой записи
- •Сортировка записей в бд по критериям
- •9.2. Применение команды Автофильтр Команда Автофильтр выполняет отбор записей по критериям одного поля.
- •Дополнительные пункты раскрывающегося списка команды Автофильтр : Все, Первые 10 , Условие…:( рис. 9.3)
- •9.3. Применение команды Расширенный фильтр
- •Глава 10. Алгоритмизация вычислительных процессов Этапы решения инженерных задач на пк
- •10.1. Алгоритм и его свойства
- •Типы алгоритмических структур
- •10.2. Линейные и разветвляющиеся алгоритмы
- •10.3. Простые циклические алгоритмы
- •10.4. Циклические алгоритмы обработки массивов
- •Двумерные массивы
- •А) ввод по строкам в) ввод по столбцам
- •Глава 11. Система программирования Visual Basic for Applications (vba)
- •11.1. Основные положения
- •11.2. Некоторые определения
- •Стандартный модуль (Module)
- •11.3. Запуск и элементы окна редактора vba
- •Глава 12. Пример создания проекта в vba и типы данных
- •12.1. Порядок действий на пк при создании проекта
- •12.2. Элементы языка vba
- •Данные в vba
- •12.3. Описание переменных
- •Глава 13. Выражения в vba и ввод – вывод данных
- •13.1. Выражения в vba
- •13.2. Операторы присваивания и способы ввода данных Оператор присваивания
- •Способы ввода данных
- •Для ввода
- •13.3. Способы вывода данных
- •Глава 14. Организация разветвляющихся программ
- •14.1. Операторы управления goto, if
- •Условный оператор управления if
- •Оператор1
- •Оператор2
- •Синтаксис многострочной формы if
- •Пример 14.2. Рассмотрим задачу, когда поставленных условий может быть больше двух:
- •Алгоритм решения задачи
- •14.2. Однострочный вложенный If
- •14.3. Оператор выбора Select Case
- •Глава 15. Организация циклических программ в vba
- •15.1. Простые циклические программы с оператором if
- •15.2. Оператор цикла For ... Next
- •15.3. Операторы циклов типа Do (выполнить)
- •Использование операторов Do While и Do Until для организация цикла с защитой входа
- •Использование операторов Do While и Do Until для организация цикла с свободным входом в цикл (с послеусловием) Организация цикла с проверкой условия в конце цикла
- •Глава 16. Массивы данных в vbа
- •16.1. Характеристики и описание одномерных массивов
- •Одномерный массив состоит из ряда элементов.
- •Синтаксис описания статического одномерного массива: dim Имя (размерность массива) [ as тип массива ]
- •Общая блок - схема обработки элементов одномерного массива
- •16.2. Примеры обработки одномерных массивов
- •Сортировка числовых одномерных массивов
- •Алгоритм сортировки одномерного массива по возрастанию
- •16.3. Двумерный массив
- •Программа
- •Глава 17. Пользовательские процедуры типа Sub и Function в vba
- •17.1. Подпрограммы
- •17.2. Процедура типа Sub Синтаксис процедуры типа Sub
- •Вызов подпрограммы процедуры Sub
- •2 Способ.
- •17.3. Подпрограмма - процедура Function
- •Вызов подпрограммы - процедуры Function
- •Глава 18. Решение оптимизационных задач
- •18.1. Обработка электронных таблиц в среде vba
- •18.2. Применение процедуры Поиск решения для решения линейных оптимизационных задач
- •18. 3. Подготовка эт
- •Список литературы
- •Глава 1. Основные понятия информатики и компьютерной техники
- •Глава 8. Обработка статистических данных в Excel
- •Глава 10. Алгоритмизация вычислительных процессов
- •Глава 17. Пользовательские процедуры типа Sub и Function в vba
7.4. Решение нелинейных уравнений в Excel
Нелинейные уравнения – это уравнения вида f(x)=0, где f(x) – нелинейная функция. Решение уравнения f(x)=0 сводится к поиску таких значений х* (корней уравнения), которые превращают уравнение в тождество. Различают нелинейные алгебраические уравнения и трансцендентные.
Например, нелинейное алгебраическое уравнение ax2 + вx +с =0 имеет два корня, которые могут быть действительными или мнимыми. Например, уравнение х2 + 2=0 имеет два мнимых корня х1= -2 и х2= --2 .
В дальнейшем будет идти речь о вычислении только действительных корней.
Трансцендентным называется уравнение, если в f(x) входит хотя бы одна трансцендентная функция. Например, sin(x) –1=0;
Решение нелинейных уравнений выполняют в два этапа:
-
Этап отделения корней.
-
Этап уточнения корней , т.е. поиск коней с заданной точностью.
Этап отделения корней
Для этого построим график заданной функции f(x)=0. В столбце А располагаем изменение аргумента, а в столбце В табулируемую функцию. Строим график. На графике выделяем границы корня и в этих границах берем начальное приближение корня (нарисовать график, выделить корни и взять начальное приближение).
Этап уточнение корня
Команда Подбор параметров
Порядок уточнения:
1. В ячейку A1 вводим начальное приближение корня Х1.
2. В ячейку В1 вводим формулу с заданной функцией.
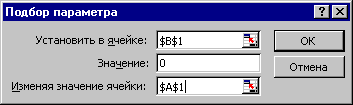
3. Выполняем команды Сервис, Подбор параметра. Появляется окно Подбор параметра (рис. 7.7).
4. В поле "Установить в ячейке" записать адрес первой формулы (можно снять окно и щелкнуть ячейку В1, затем восстановить окно).
5. В поле "Значение" установить 0.
6. В поле "Изменяя значение ячейки" установить адрес А1 (снять окно и щелкнуть А1).
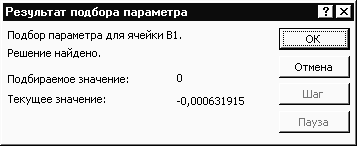
7. Щелкнуть ОК. Появляется окно Результат подбора параметра (рис. 7.8), а в ячейке А1 будет уточненное значение корня.
Рис.
7.8
Рис.
7.7
7.5. Вычисления по итерационным формулам
Итерационной
называется формула типа yi+1
= f
(yi)
. Пример1.
Вычисление
![]() задано итерационной формулой yi+1=(x/yi2
+2yi)/3
задано итерационной формулой yi+1=(x/yi2
+2yi)/3
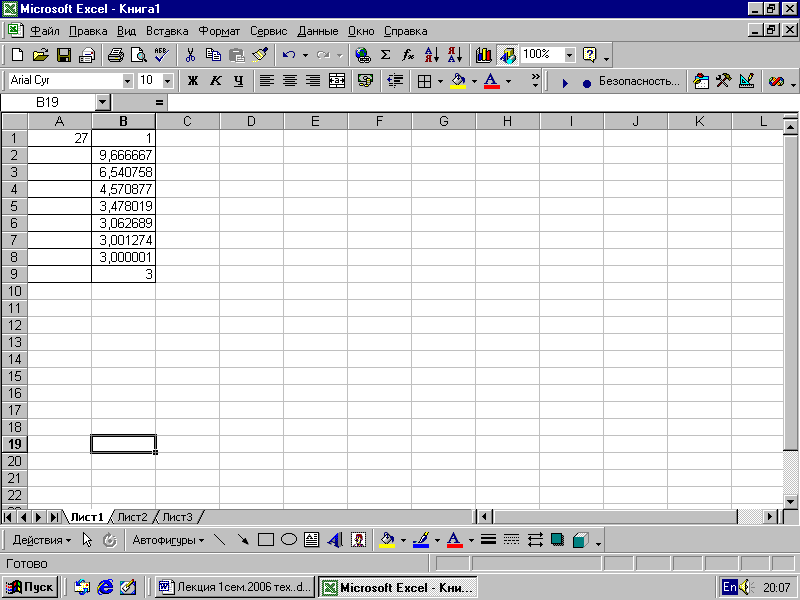
Начальное приближении у0=1 и значение х= 27.
Составим ЭТ для вычисления:
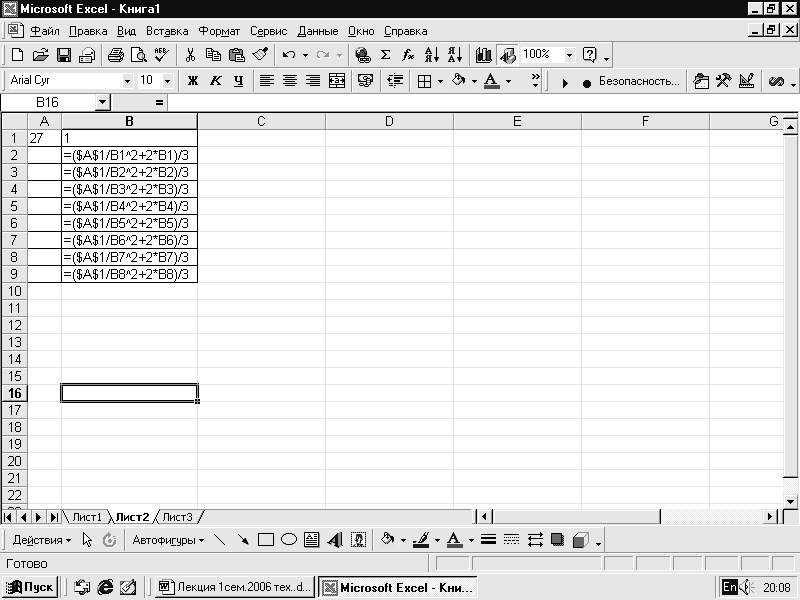
1. В ячейку a2 запишем значение х равное 27 (рис. 7.9).
2. В ячейку b2 запишем значение у0 равное 1.
3
Рис.
7.9
Пример 2. Заданы итерационные формулы
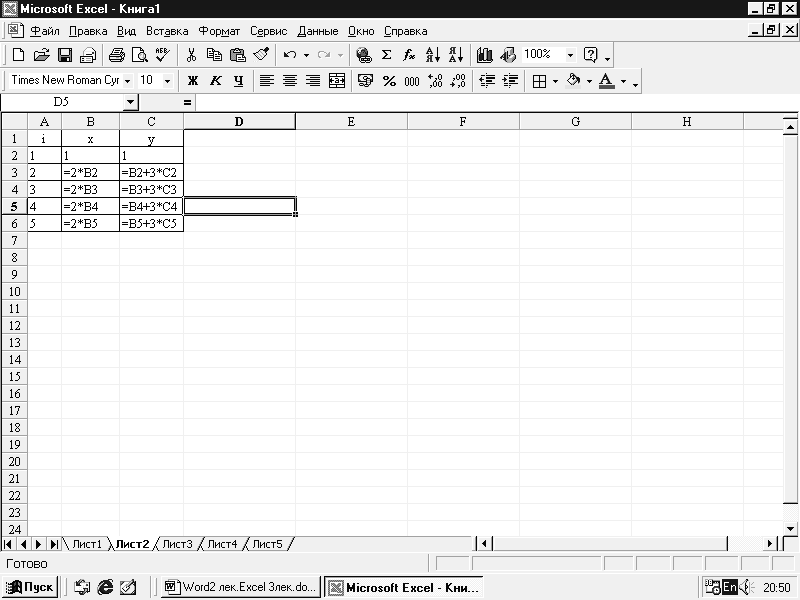
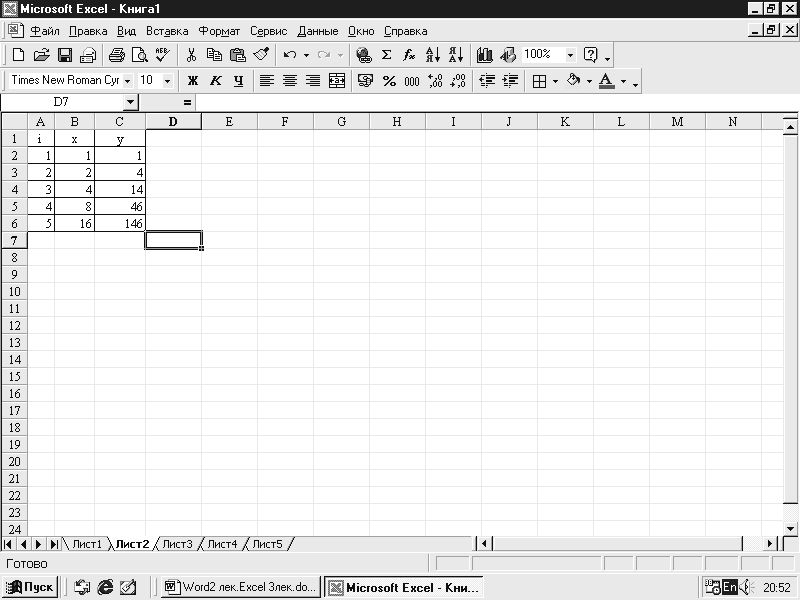
x i =2xi-1 и yi= xi-1 + 3yi-1 при изменении i=2,3,4,5.
При i=2 х2 = 2х1 и y2= x1 + 3y1
Начальные значения x1=1 ; y1=1 (рис. 7.10) запишем в В2 и С2 соответственно. В ячейки В3 и С3 запишем формулы для х2 и у2 . Выделяем В3:С3 и копируем вниз до С6. Результат вычисления на рис. 7.11.
Рис.
7.10
Рис.
7.11
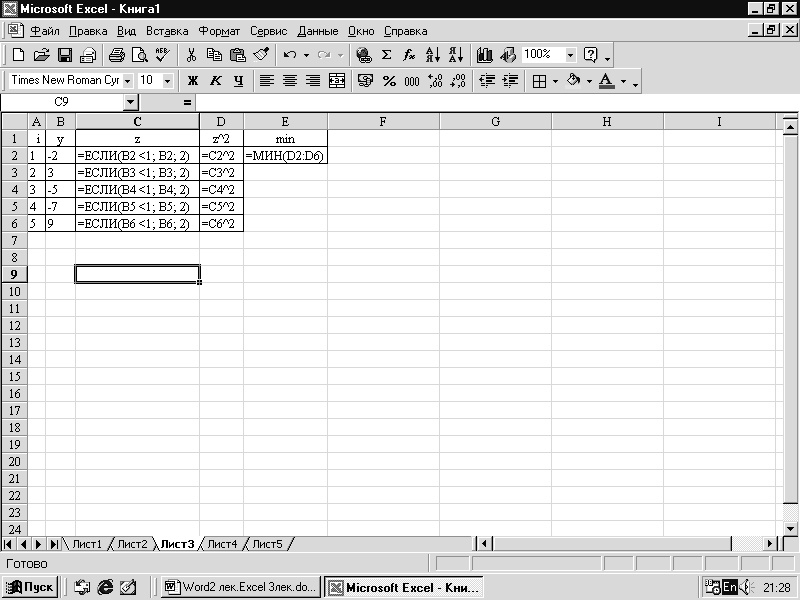
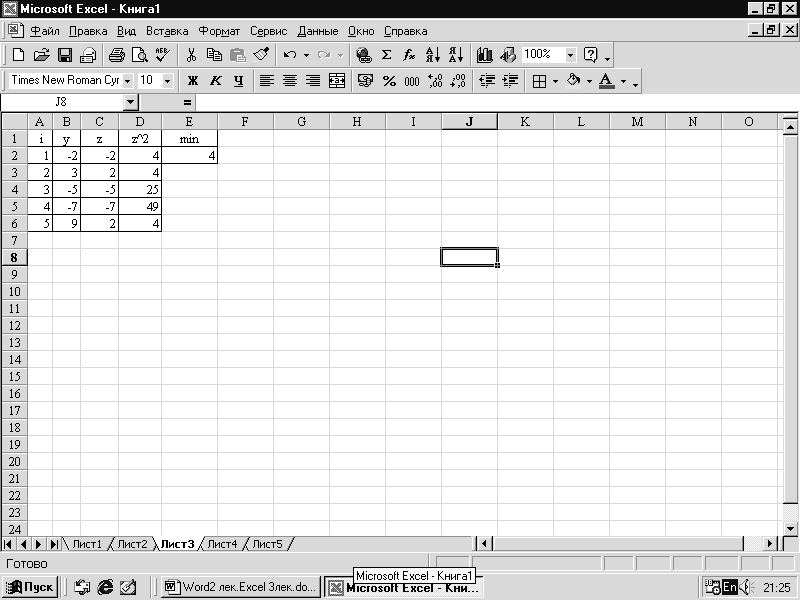
Пример 3.
Решение задач следующего типа:
Даны действительные числа у1, у2,…у5, которые записаны в В2:В6
Составить ЭТ для вычисления
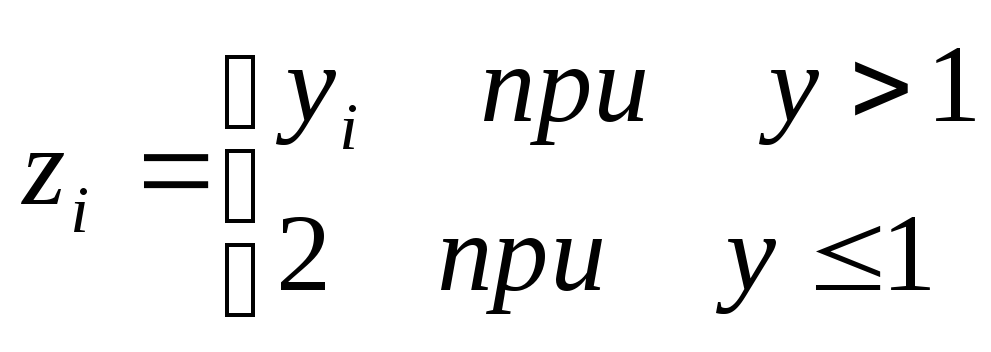 и
определения min(z12,
z22,
…,z52)
при i=1,2,…,5
и
определения min(z12,
z22,
…,z52)
при i=1,2,…,5
Рис.
7.12