
- •Математическое моделирование (Катанов Юрий Евгеньевич) Лабораторная работа №1.
- •Варианты заданий:
- •Лабораторная работа №2.
- •Варианты заданий:
- •Лабораторная работа №3.
- •Варианты заданий:
- •Лабораторная работа №4.
- •Варианты заданий:
- •Лабораторная работа №5.
- •Варианты заданий:
- •Лабораторная работа №6.
- •Варианты заданий:
- •Варианты заданий:
- •Варианты заданий:
- •Лабораторная работа №7.
- •Варианты заданий:
- •Варианты заданий:
- •Варианты заданий:
- •Лабораторная работа №8.
- •Варианты заданий:
- •Варианты заданий:
- •Варианты заданий:
- •Лабораторная работа №9.
- •Варианты заданий:
- •Варианты заданий:
- •Варианты заданий:
- •Варианты заданий:
- •Варианты заданий:
- •Лабораторная работа №10.
- •Варианты заданий:
- •Варианты заданий:
Варианты заданий:
|
1 вариант |
|
|
2 вариант |
|
|
3 вариант |
|
|
4 вариант |
|
|
5 вариант |
|
|
6 вариант |
|
|
7 вариант |
|
|
8 вариант |
|
|
9 вариант |
|
|
10 вариант |
|
|
11 вариант |
|
|
12 вариант |
|
|
13 вариант |
|
|
14 вариант |
|
|
15 вариант |
|
Задача
4:
В резервуаре вместимостью
 м3
находится рассол, содержащий
м3
находится рассол, содержащий
 кг растворенной соли. В резервуар
вливается вода со скоростью
кг растворенной соли. В резервуар
вливается вода со скоростью
 м3/мин,
а из него вытекает со скоростью
м3/мин,
а из него вытекает со скоростью
 м3/мин,
причем концентрация поддерживается
однородной посредством перемешивания.
Сколько соли содержится в резервуаре
по истечении времени
м3/мин,
причем концентрация поддерживается
однородной посредством перемешивания.
Сколько соли содержится в резервуаре
по истечении времени
 .
.
Решение:
Для
примерных расчетных данных,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
используя (9.2) определим изменение объема
резервуара с учетом различных скоростей
втекания и вытекания воды:
,
используя (9.2) определим изменение объема
резервуара с учетом различных скоростей
втекания и вытекания воды:
 . (9.3)
. (9.3)
Для
расчетных данных,
 .
.
Таким образом, когда скорости втекания и вытекания в резервуар не совпадают, то (7.6) примет вид:
 , (9.4)
, (9.4)
где
 - скорость вытекания из резервуара.
- скорость вытекания из резервуара.
Для
данных значений, (9.4) примет вид:
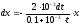 .
.
Разделяя переменные и интегрируя последнее равенство, получаем следующее:
 ,
,
 ,
,
 ,
,
 ,
,
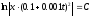 ,
,
 ,
,
 .
.
Используя
начальное условие, а именно, в начальный
момент времени масса соли была равна
10 кг, т.е.
 ,
находим постоянную величину
,
находим постоянную величину
 :
:
 ,
,
 ,
,
 .
.
Тогда,
по истечении времени
 ,
в резервуаре останется количество соли,
равное
,
в резервуаре останется количество соли,
равное
 .
.
Варианты заданий:
|
1 вариант |
|
|
2 вариант |
|
|
3 вариант |
|
|
4 вариант |
|
|
5 вариант |
|
|
6 вариант |
|
|
7 вариант |
|
|
8 вариант |
|
|
9 вариант |
|
|
10 вариант |
|
|
11 вариант |
|
|
12 вариант |
|
|
13 вариант |
|
|
14 вариант |
|
|
15 вариант |
|
Задача
5: Воздух
в помещении вместимостью
 м3
содержит
м3
содержит
 %
%
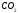 .
В помещении равномерно поступает чистый
воздух, содержащий
.
В помещении равномерно поступает чистый
воздух, содержащий
 %
%
 .
Сколько кубических метров воздуха
ежеминутно поступает в помещение, если
по истечении времени
.
Сколько кубических метров воздуха
ежеминутно поступает в помещение, если
по истечении времени
 содержание
содержание
 падает
до
падает
до
 %.
Найти закон изменения объема
%.
Найти закон изменения объема
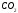 с течением времени, если единицу времени
в помещение поступает
с течением времени, если единицу времени
в помещение поступает
 м3
воздуха.
м3
воздуха.
Решение:
для
примерных данных,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
получаем, что
,
получаем, что
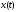 -
объем
-
объем
 в момент времени
в момент времени

 ,
а
,
а
 -
объем
-
объем
 в начальный момент времени
в начальный момент времени

 ,
который определяется следующим образом:
,
который определяется следующим образом:
 . (9.5)
. (9.5)
Для
данных значений он равен
 ,
а по истечении 10 минут он будет равен
,
а по истечении 10 минут он будет равен
 .
.
Тогда
изменение объема
 в помещении определяется зависимостью:
в помещении определяется зависимостью:
 , (9.6)
, (9.6)
где
 -
концентрация
-
концентрация
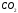 в
чистом воздухе.
в
чистом воздухе.
Тогда
для приведенных данных,
 ,
, .
.
Разделяя переменные и интегрируя, получаем:
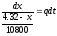 ,
,
 ,
,
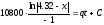 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Так
как в начальный момент времени, объем
 был
равен 12.96 м3,
то подставляя это значение в последнее
равенство, получим неизвестную величину
был
равен 12.96 м3,
то подставляя это значение в последнее
равенство, получим неизвестную величину
 :
:
 ,
,
 ,
,
 .
.
Следовательно,
 .
.
Так
как по истечении 10 минут, объем
 стал
равен 6.48 м3,
то найдем величину
стал
равен 6.48 м3,
то найдем величину
 :
:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
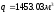 .
.
Тогда
закон изменения объема
 с течением времени, если единицу времени
в помещение поступает
с течением времени, если единицу времени
в помещение поступает
 м3
воздуха,
принимает вид:
м3
воздуха,
принимает вид:
 ,
,
![]() .
.

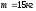 ,
,
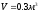 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
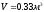 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
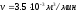 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
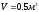 ,
,
 ,
,
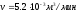 .
. ,
,
 ,
,
 ,
,
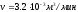 .
. ,
,
 ,
,
 ,
,
 .
. ,
,
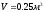 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 ,
,
 .
. ,
,
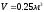 ,
,
 ,
,
 ,
,

 ,
,
 ,
,
 ,
,
 ,
,

 ,
,
 ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 ,
,
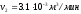 .
. ,
,
 ,
,
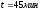 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
 ,
,
 .
. ,
,
 ,
,
 ,
,
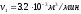 ,
,
 .
. ,
,
 ,
,
 ,
,
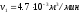 ,
,
 .
.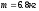 ,
,
 ,
,
 ,
,
 ,
,
 .
.