Варианты заданий:
|
1 вариант |
|
|
2 вариант |
|
|
3 вариант |
|
|
4 вариант |
|
|
5 вариант |
|
|
6 вариант |
|
|
7 вариант |
|
|
8 вариант |
|
|
9 вариант |
|
|
10 вариант |
|
|
11 вариант |
|
|
12 вариант |
|
|
13 вариант |
|
|
14 вариант |
|
|
15 вариант |
|
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
Задача
3:
Определить равновесный размер популяции,
если на
особей
в единицу времени,
особей
рождается, а гибнет
.
Предполагается при этом, что начальная
численность популяции равна
особям.
Построить график логистической кривой.
Решение:
Определим
величины
,
,
,
,
.
Тогда согласно модели Мальтуса
,
найдем соответствующие составляющие,
при этом разделим переменные и
проинтегрируем:
.
Работаем с правой частью последнего равенства:
.
Подставляя
в последнее равенство:
,
,
,
.
,
.
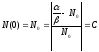Чтобы
не путать с рождаемостью, обозначим
параметр
,
стоящий под степенью экспоненты как
,
являющийся характеристикой
пропорциональности роста численности
популяции. Для его нахождения, используем
тот же подход, что и в задачи 1.
а)
если
,
,
.
б)
если
,
,
.
.
,
поэтому используем формулу
.
Варианты заданий:
|
1 вариант |
|
|
2 вариант |
|
|
3 вариант |
|
|
4 вариант |
|
|
5 вариант |
|
|
6 вариант |
|
|
7 вариант |
|
|
8 вариант |
|
|
9 вариант |
|
|
10 вариант |
|
|
11 вариант |
|
|
12 вариант |
|
|
13 вариант |
|
|
14 вариант |
|
|
15 вариант |
|
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
Лабораторная работа №9.
Цель: математические модели прикладных задач (растворение веществ)
Задача
1: Нерастворимое
вещество, содержащее в своих порах
кг
соли, подвергается действию
л
воды. Через время
,
кг
соли растворяется. Через сколько времени
растворится
первоначальной массы соли, если
концентрация насыщенного раствора
равна
.
Решение:
Пусть
-
масса нерастворенной соли в момент
времени
.
Процесс растворения веществ описывается
уравнением:
, (9.1)
где
- коэффициент пропорциональности;
-
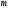первоначальная масса соли.
Тогда
для примерных расчетных данных:
,
,
,
,
,
,
,
.
Величина
,
получилась из тех соображений, что
изначально нерастворимое вещество
содержало 2кг соли, а поскольку необходимо
определить время растворения 99 %
первоначальной массы соли, то на
оставшийся 1 % нерастворенной соли
останется как раз
.
Подставляя в (9.1) примерные данные, находим:
,
,
,
.
Разделим переменные и проинтегрируем последнее равенство:
.
Левую
часть равенства получим с помощью метода
неопределенных коэффициентов:
,
.
Поскольку знаменатели равны, приравняем
и числители:
.
Раскроем
скобки в последнем равенстве, сгруппируем
коэффициенты при соответствующих
степенях переменной и приравняем данные
сгруппированные коэффициенты в правой
части к степеням в левой части равенства:
,
,
.
Подставляя в исходное равенство найденные коэффициенты:
.
Интегрируя до конца (7.5), получаем
,
,
,
,
,
. (*)
Используя начальные условия, находим неизвестные величины, используя равенство (*):
,
,
.
,
,
,
,
,
.
Итоговый вид уравнения (*) следующий:
.
Теперь
подставляя вместо
величину
,
находим итоговое время для растворения
99 % первоначальной массы соли:
,
,
,
.
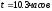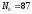
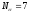
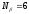