Глава 3. Физическое и математическое моделирование технических систем

3.1 Общие положения

Любая модель технической системы есть некоторые нетождественный аналог её. Быть аналогом системы означает быть подобной ей. Подобие различных систем может быть физическим и математическим.

Все процессы, протекающие в физически подобных системах, имеют одинаковую физическую природу.

У математически подобных объектов процессы могут иметь разную физическую природу, но описываются одинаковыми математическими уравнениями.

Подобность систем – это условие, при котором можно перенести количественные результаты исследований на модели на оригинал.

Физическая подобность обусловливает традуктивность моделирования, т.е. возможность установления масштабных коэффициентов, что и позволяет оценивать поведение объекта по результатам исследования модели. Правило традукции: безразмерные комплексы (критерии подобия) в сходственных точках подобных объектов (т.е. модели и оригинала) равны. Возможности физического моделирования сложных систем ограничены. Поэтому в ряде случаев применяются принципы аналогии, т.е. сходство нетождественных объектов в некоторых отношениях. Аналогичными можно считать процессы, имеющие различную физическую природу, но описываемые сходными математическими уравнениями. Приведём примеры.

Закон Ньютона для движения вязкой жидкости:

r = ,

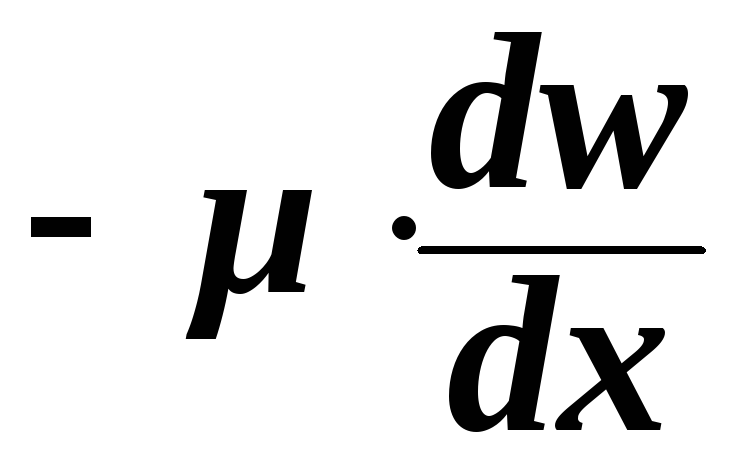где r – поток импульса, μ – коэффициент вязкости.

Закон Фурье для переноса тепла:

q = ,

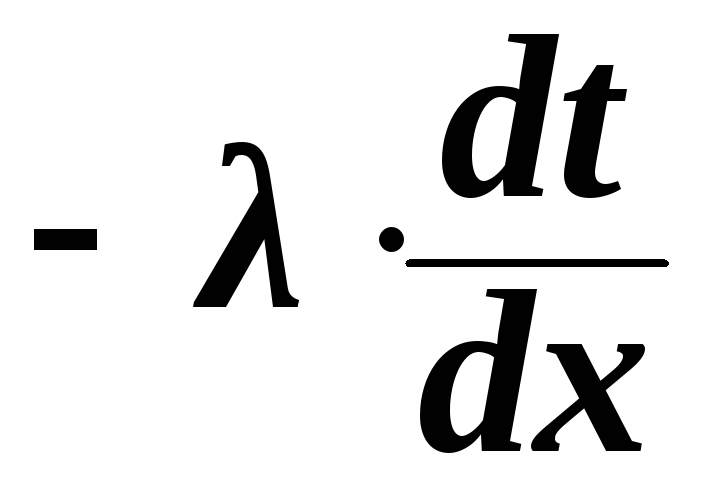где q – тепловой поток, λ – коэффициент теплопроводности.

Закон Фика для переноса вещества:

g = ,

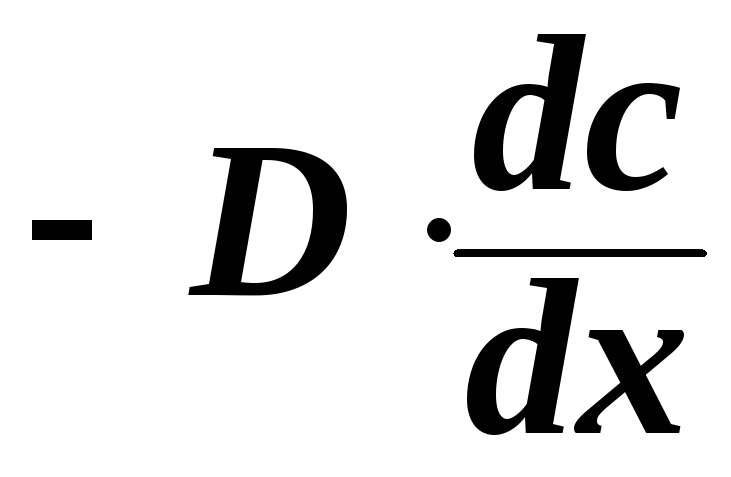где g – поток вещества, D – коэффициент диффузии.

Закон Ома для переноса электричества:

,

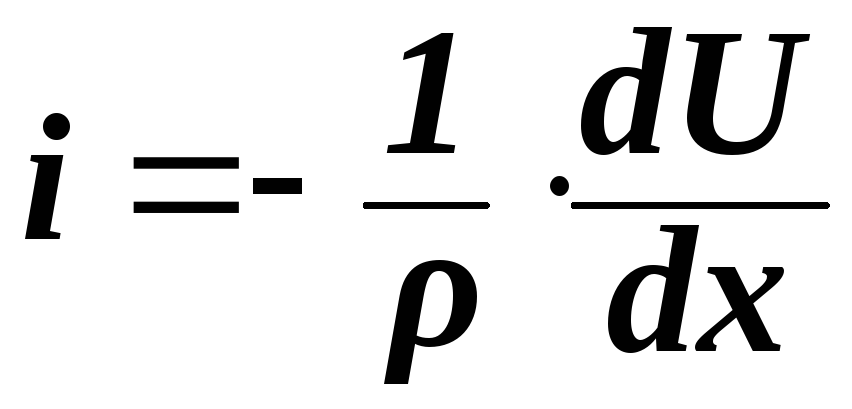где і – ток, ρ – коэффициент сопротивления.

Все приведённые уравнения описывающие, соответственно, перенос энергии, тепла, вещества в потоке и электричества, содержат градиенты, соответственно, скорости , температуры , концентрации и напряжения . Если ввести пересчётные коэффициенты, то любое из этих явлений можно смоделировать переносом электричества.

Аналогия расширяет возможности моделирования по сравнению с теорией физического подобия, однако не устраняет многих трудностей, связанных с условиями моделирования сложных технических систем. Эти трудности удаётся преодолеть при математическом моделировании.

Если систему (процесс, явление) можно описать математически в виде системы уравнений, а результат решения этих уравнений, выполненного в соответствии с определённым алгоритмом, можно перенести на оригинал, то эта система уравнений и есть математической моделью.

Физическое моделирование эффективно при изучении детерминированных процессов, в которых определяющие их величины изменяются по определённым законам. Целью физического моделирования является воспроизведение в меньших масштабах процессов, протекающих в изучаемых системах, при непрерывно изменяющихся параметрах, входящих в математические формулировки законов, которым подчиняются процессы.

Математическое моделирование применяется для описания с помощью математических моделей различных технических систем и технологических процессов, в том числе и стохастических.

Физическое и математическое моделирование не противопоставляется, а дополняет друг друга. При этом математическое моделирование, которое рассматривает целый класс аналогичных явлений, описываемых одним и тем же уравнением, является более общим, чем моделирование физическое.

Итак, математическое моделирование – это способ описания процессов с количественной и качественной стороны с помощью математической моделей, а математическая модель – это математическое описание процесса с помощью математического аппарата. Математическая модель представляет собой систему уравнений, отражающую сущность явлений, протекающих в изучаемом объекте.