4.2. Двойственный симплекс-метод
Рассмотрим задачу на максимум, у которой в строке целевой функции в симплексной таблице все элементы неотрицательные, а в столбце bj могут находиться как положительные, так и отрицательные значения переменных. Такая задача является двойственно допустимой, но решение основной задачи недопустимо (так как в столбце bj находятся отрицательные значения переменных). Суть двойственного симплекс-метода состоит в том, чтобы последовательно привести задачу к допустимому базисному решению, при этом итерации строить так, чтобы в строке ЦФ сохранялось допустимое решение двойственной задачи (элементы строки ЦФ должны остававаться неотрицательными). Алгоритм двойственного симплекс-метода будет следующим.
1. Сначала выбирается разрешающая строка: базис покинет та переменная, которая имеет наибольшее отрицательное значение переменной.
2. Для определения разрешающего столбца рассчитываются отрицательные симплексные отношения: значения в строке ЦФ делятся на соответствующие отрицательные элементы разрешающей строки. Из них выбирается минимальное по модулю, которое и определяет разрешающий столбец.
3. Выполняются преобразования Жордана-Гаусса. Итерации выполняются до тех пор, пока все значения базисных переменных основной задачи не станут положительными.
Замечание. Для решения задач на минимум двойственным симплекс-методом необходимо умножить целевую функцию на (–1) и решать задачу на максимум.
Например, рассмотрим задачу (9) – двойственную к задаче о мебельной фабрике. Умножим ЦФ W на (–1), чтобы задача стала на max и преобразуем ее к стандартному виду, и умножим все ограничения на (–1), чтобы избыточные переменные ei имели положительный коэффициент:
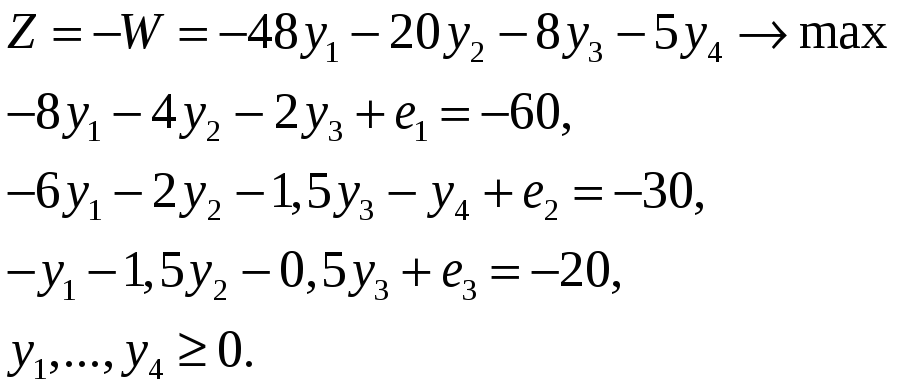
Пусть необходимо решить данную задачу. Для решения этой задачи обычным симплекс-методом необходимо прибегнуть к методу искусственного базиса, поскольку выделить исходный допустимый базис сразу нельзя. Будем решать задачу двойственным симплекс-методом, взяв в качестве исходного базиса недопустимые значения: e1 = –60, e2 = –30, e3 = – 20. Построим симплексную таблицу, в которой вместо столбца с симплексными отношениями будет строка с симплексными отношениями.
|
Базис |
cj |
|
y1 |
y2 |
y3 |
y4 |
e1 |
e2 |
e3 |
|
–48 |
–20 |
–8 |
–5 |
0 |
0 |
0 |
|||
|
1) e1 |
0 |
–60 |
–8 |
–4 |
–2 |
0 |
1 |
0 |
0 |
|
2) e2 |
0 |
–30 |
–6 |
–2 |
–1,5 |
–1 |
0 |
1 |
0 |
|
3) e3 |
0 |
–20 |
–1 |
–1,5 |
–0,5 |
0 |
0 |
0 |
1 |
|
|
0 |
48 |
20 |
8 |
5 |
0 |
0 |
0 |
|
|
с. о. |
48/8=6 |
20/4=5 |
8/2=4 |
– |
– |
– |
– |
||
Заметим, что в индексной строке все значения неотрицательные, а значит, двойственная задача имеет допустимое текущее решение и двойственный симплекс-метод можно применить.
Переменная e1 в первую очередь покинет базис, поскольку имеет максимальное по модулю отрицательное значение (–60). Переменная y3 войдет в базис вместо e1, так как в столбце y3 минимальное симплексное отношение. Далее симплексная таблица пересчитывается обычным образом.
|
Базис |
cj |
|
y1 |
y2 |
y3 |
y4 |
e1 |
e2 |
e3 |
|
–48 |
–20 |
–8 |
–5 |
0 |
0 |
0 |
|||
|
1) y3 |
–8 |
30 |
4 |
2 |
1 |
0 |
–0,5 |
0 |
0 |
|
2) e2 |
0 |
15 |
0 |
1 |
0 |
–1 |
–0,75 |
1 |
0 |
|
3) e3 |
0 |
–5 |
1 |
–0,5 |
0 |
0 |
–0,25 |
0 |
1 |
|
|
–240 |
16 |
4 |
0 |
5 |
4 |
0 |
0 |
|
|
с. о. |
– |
4/0,5=8 |
– |
– |
– |
– |
– |
||
|
Базис |
cj |
|
y1 |
y2 |
y3 |
y4 |
e1 |
e2 |
e3 |
|
–48 |
–20 |
–8 |
–5 |
0 |
0 |
0 |
|||
|
1) y3 |
–8 |
10 |
8 |
0 |
1 |
0 |
–1,5 |
0 |
4 |
|
2) e2 |
0 |
5 |
2 |
0 |
0 |
–1 |
–1,25 |
1 |
2 |
|
3) y2 |
–20 |
10 |
–2 |
1 |
0 |
0 |
0,5 |
0 |
–2 |
|
|
–280 |
24 |
0 |
0 |
5 |
2 |
0 |
8 |
|
Таким образом, получили решение y1 = y4 = 0, y2 = y3 = 10, W = –Z = 280, что совпадает с решением, полученным в табл. 3.4.