Условия равновесия произвольной плоской системы сил. Случай параллельных сил.

Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия: R = 0, M₀ = 0.

Здесь О - любая точка плоскости.

Найдем вытекающие из равенств аналитические условия равновесия.

Величины R и М_о определяются равенствами:

где Но R может равняться нулю только тогда, когда одновременно R_x = 0 и R_y = 0. Следовательно, условия будут выполнены, если будет:

Равенства выражают, следующие аналитические условия рав­новесия: для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на каж­дую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.

Теорема о трех моментах. Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю.

; ;

Равновесие плоской системы параллельных сил.

В случае, когда все действующие на тело силы параллельны друг другу, мы можем направить ось Ох перпендикулярно к силам, а ось Оу параллельно им (рис. 29). Тогда проекция каждой из сил на Ox будет равна нулю и первое из 3-х равенств обратится в тождество вида 0 = 0. В результате для параллельных сил останется два условия равновесия:

Где ось Оу параллельна силам

Предельная сила трения

Изучение равновесия тел с учетом трения сводится обычно к рассмотрению предельного положения равновесия, когда сила трения достигает своего наиболь­шего значения . При аналитическом решении задач реакцию шероховатой связи в этом случае изображают двумя составляющими N и , где . Затем составляют обычные условия равновесия статики, подставляют в них вместо величину и, решая полу­ченные уравнения, определяют искомые величины.

Коэффициент трения

Коэффициент трения - отношение силы трения F к реакции Т, направленной по нормали к поверхности касания, возникающей при приложении нагрузки, прижимающей одно тело к другому: f = F/T.

Коэффициент трения — характеристика, применяемая при выполнении технических расчётов, характеризующих фрикционное взаимодействие двух тел. В зависимости от вида перемещения одного тела по другому различают: коэффициент трения при сдвиге — скольжении и коэффициент трения при качении. В свою очередь, при скольжении в зависимости от величины тангенциальной силы различают коэффициент неполного трения скольжения, коэффициент трения покоя и коэффициент трения скольжения. Все эти коэффициенты трения могут изменяться в широких пределах в зависимости от шероховатости и волнистости поверхностей, характера плёнок, покрывающих поверхности. Для протяжённого контакта они мало изменяются с изменением нагрузки. В зависимости от величины коэффициент трения скольжения пары трения делят на 2 группы: фрикционные материалы, имеющие большой коэффициент трения— обычно 0,3—0,35, редко 0,5—0,6, и антифрикционные, имеющие коэффициент трения без смазки 0,15—0,12, при граничной смазке 0,1—0,05. Сопротивление свободному качению твёрдого тела (например, колеса) характеризуют коэффициентом сопротивления перекатыванию fk = T•rd/Ik [см], где Т — нормальная составляющая реакции колеса на опору; rd — динамический радиус качения; Ik — нормальная нагрузка на колесе. Если на колесо действуют ведущий или тормозной моменты, то коэффициент сцепления y колеса с дорожным покрытием определяется равенством: y = Tx/Ik, где Tx — неполная сила трения скольжения, возникающая между катящимся колесом и дорогой. Коэффициенты fk и y существенно зависят от природы трущихся тел, характера покрывающих их плёнок и скорости качения. Обычно для металлов (сталь по стали) fk = 0,001—0,002 см. При движении автомобиля со скоростью 80 км/час коэффициент трения колёс по асфальту fk = 0,02 см и резко возрастает с увеличением скорости. Коэффициент сцепления y на сухом асфальте доходит у автомобильных колёс до 0,8, а при наличии плёнки воды снижается до 0,2—0,1.

Коэффициент трения зависит от рода грунта и скорости относительного перемещения трущихся поверхностей. Коэффициент трения покоя (табл. 8.1) несколько больше коэффициента трения в момент получения движения судном при снятии с мели. Таблица 8.1 Величины коэффициента трения покоя для различных грунтов Характер грунта Коэффициент Жидкая глина (ил) Глина Глина с песком Мелкий песок Крупный песок Галька Каменная плита Булыжник 0,20—0,30 0,30—0,45 0,30—0,40 0,40—0,45 0,40—0,50 0,45—0,50 0,35—0,50 0,40—0,60 При посадке на мель, как правило, корпус судна проседает в грунте. Грунт начинает оказывать давление на борта судна. Это давление является причиной дополнительного сопротивления стаскиванию судна с мели. Величина проседания зависит от рода грунта, силы давления корпуса, времени нахождения на мели. При проседании судна частицы грунта прилипают к корпусу, создавая эффект присасывания. Сила присасывания тем больше, чем большей вязкостью обладает грунт. Наибольшее присасывание наблюдается у вязкой глины. На каменистых грунтах корпус может получить пробоины, в которые проникают камни и даже скалы. Это также препятствует снятию судна с мели. Характер сил, действующих на судно, находящееся на мели, разнообразен, но учет их возможен. Однако для этого требуются громоздкие расчеты, основанные на всестороннем и тщательном обследовании состояния судна, что само по себе является трудоемким процессом. В практике пользуются упрощенными расчетами по формуле (8.1) и принимают во внимание особенности действия сил. Этого достаточно, чтобы принять принципиальное решение о возможности снятия судна с мели собственными средствами и оценить характер и объем аварийных работ

Момент силы относительно оси

 

Моментом силы относительно оси (рис. 1.25), назы­вается алгебраиче­ская величина, абсолютное значение которой равняется произведению модуля проекции силы на плоскость , перпендикулярную к оси , на расстояние от точ­ки пересечения оси с этой плоскостью до линии действия проекции силы на плоскость , т.е.

 

.

 

Знак "плюс'' - если направление вращения силы вокруг точки с конца оси видно происходящим против часовой стрелки, если по ча­совой стрелке, то знак "минус''. Очевидно, что момент силы относительно оси равен нулю, если линия действия силы и ось лежат в одной плоскости.

В случае пространственной системы сил главным моментом относительно точки называется векторная сумма моментов всех сил системы относительно той же точки:

 

.

 

Главным моментом пространственной системы сил относитель­но оси назы­вается сумма моментов всех сил системы относительно этой оси:

 

 

Зная главные моменты системы сил относительно осей декар­товых коорди­нат, можно вычислить модуль главного момента отно­сительно начала коорди­нат и его направляющие косинусы

 

,

; ; .
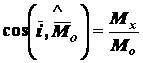