
- •Статика Аксиомы статики.
- •Связи и их реакции.
- •Проекция силы на ось и на плоскость.
- •Равновесие системы сходящихся сил.
- •Момент силы относительно центра (или точки).
- •Пара сил. Момент пары.
- •Условия равновесия произвольной плоской системы сил. Случай параллельных сил.
- •Предельная сила трения
- •Коэффициент трения
- •Условия равновесия пространственной системы сил
- •Координаты центра тяжести
- •Кинематика
- •Полное ускорение при криволинейном движении
- •Графики движения
- •Скорости и ускорения точек вращающегося тела.
- •Составляющие сложного движения тел, определения
- •Динамика Законы и задачи динамики
- •Задачи динамики для свободной и несвободной материальной точки.
- •Основные виды сил в механике
- •Дифференциальные уравнения движения точки
- •Алгоритм решения задач динамики точки
- •Работа силы.
- •Мощность.
- •Кинетическая энергия
- •Относительное, переносное и абсолютное движение точки
- •Момент инерции
- •Теорема Гюйгенса-Штейнера
Момент инерции
Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Моменты
инерции однородных тел простейшей
формы относительно некоторых осей
вращения Тело Описание Положение оси
a Момент инерции Ja
![]() Материальная
точка массы m На расстоянии r от
точки, неподвижная
Материальная
точка массы m На расстоянии r от
точки, неподвижная
![]()
 Полый
тонкостенный цилиндр или кольцо радиуса
r и массы m Ось цилиндра
Полый
тонкостенный цилиндр или кольцо радиуса
r и массы m Ось цилиндра
![]()
 Сплошной
цилиндр или диск радиуса r и массы
m Ось цилиндра
Сплошной
цилиндр или диск радиуса r и массы
m Ось цилиндра
![]()
 Полый
толстостенный цилиндр массы m с
внешним радиусом r2 и
внутренним радиусом r1 Ось
цилиндра
Полый
толстостенный цилиндр массы m с
внешним радиусом r2 и
внутренним радиусом r1 Ось
цилиндра
![]()
 Сплошной
цилиндр длины l, радиуса r и массы
m Ось перпендикулярна к цилиндру и
проходит через его середину
Сплошной
цилиндр длины l, радиуса r и массы
m Ось перпендикулярна к цилиндру и
проходит через его середину
![]()
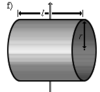 Полый
тонкостенный цилиндр (кольцо) длины l,
радиуса r и массы m Ось перпендикулярна
к цилиндру и проходит через его середину
Полый
тонкостенный цилиндр (кольцо) длины l,
радиуса r и массы m Ось перпендикулярна
к цилиндру и проходит через его середину
![]()
 Прямой
тонкий стержень длины l и массы m
Ось перпендикулярна к стержню и проходит
через его середину
Прямой
тонкий стержень длины l и массы m
Ось перпендикулярна к стержню и проходит
через его середину
![]()
 Прямой
тонкий стержень длины l и массы m
Ось перпендикулярна к стержню и проходит
через его конец
Прямой
тонкий стержень длины l и массы m
Ось перпендикулярна к стержню и проходит
через его конец
![]()
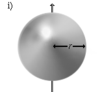 Тонкостенная
сфера радиуса r и массы m Ось
проходит через центр сферы
Тонкостенная
сфера радиуса r и массы m Ось
проходит через центр сферы
![]()
 Шар
радиуса r и массы m Ось проходит
через центр шара
Шар
радиуса r и массы m Ось проходит
через центр шара
![]()
 Конус
радиуса r и массы m Ось конуса
Конус
радиуса r и массы m Ось конуса
![]()
Теорема Гюйгенса-Штейнера
Основная статья: Теорема Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
![]()
Если
![]() —
момент инерции тела относительно оси,
проходящей через центр
масс тела, то момент инерции
относительно параллельной оси,
расположенной на расстоянии
—
момент инерции тела относительно оси,
проходящей через центр
масс тела, то момент инерции
относительно параллельной оси,
расположенной на расстоянии
![]() от
неё, равен
от
неё, равен
![]() ,
,
где
![]() —
полная масса тела.
—
полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

