§3. Число сочетаний, размещений и размещений с повторениями

Пусть – число всех –размещений с повторениями.

Теорема 2.

Доказательство. Пусть . Между множеством –размещений с повторениями и прямым произведением существует взаимно однозначное соответствие, т.е. они равномощны. По следствию теоремы 1 имеем , т.е. число всех размещений с повторениями из n по k равно .

Число всех –размещений обозначается через .

Теорема 3. .

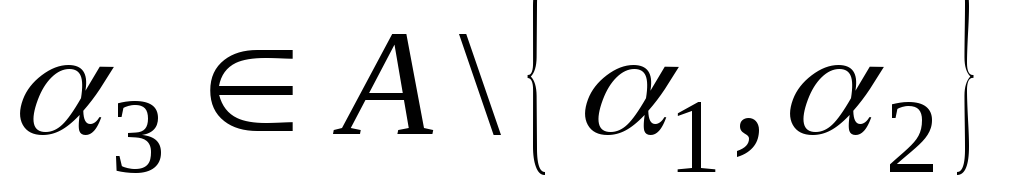Доказательство. Пусть – –размещение из множества , где , , для всех . Элемент может быть выбран n способами, , т.е. после выбора элемента элемент может быть выбран способом, после выбора и выбираем элемент , он может быть выбран способами и т.д. После выбора элементов ,,…, последний элемент может быть выбран способами.

По правилу произведения получаем, что число всех –размещений равно .

Пусть – число всех перестановок из элементов.

Следствие. .

Число всех –сочетаний обозначается через или . Эта величина называется биномиальным коэффициентом.

Теорема 4.

Доказательство. Рассмотрим –сочетание , эту неупорядоченную –выборку можно упорядочить способами ( в силу следствия теоремы 3). Если упорядочить каждое –сочетание, то получим все упорядоченные –выборки, т.е. . Отсюда получаем, что .

Задача 3. Сколько существует двоичных матриц с строками и столбцами, все строки которых различны?

Решение. Число различных двоичных упорядоченных наборов длины равно . Число всех двоичных матриц с строками совпадает с числом всех размещений из элементов по . Следовательно, по теореме 3 получаем, что число матриц равно .

Задача 4. Сколькими способами из колоды в 36 карт можно вытащить 5 карт так, чтобы среди них были три карты червовой масти и две крестовой масти?

Решение. Всего в колоде имеем по 9 карт каждой из 4 мастей. Три карты червовой масти можем вытащить способами, а две карты крестовой масти можно вытащить способами. По правилу произведения получаем, что существует  способов вытащить из колоды 5 карт определенным образом.

§4. Основные свойства биномиальных коэффициентов

Свойство 1. .

Доказательство. Рассмотрим множество из n элементов . Каждому –сочетанию однозначно соответствует –сочетание , составленное из элементов множества 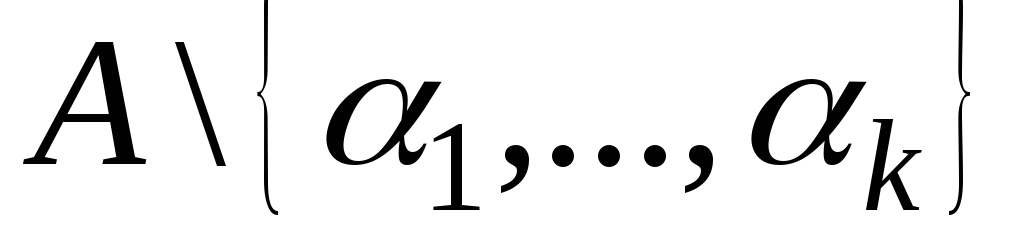. Отсюда следует, что число –сочетаний и число –сочетаний одинаково.

Убедиться в справедливости свойства 1 можно также непосредственной проверкой, расписав число сочетаний по теореме 4.

Свойство 2. .

Доказательство. Свойство доказывается непосредственной проверкой. Согласно теореме 4 имеем , . Отсюда получаем, что

.

Свойство 3.

Доказательство. Пусть . Число всех подмножеств множества А равно , число всех k–элементных подмножеств множества А равно , тогда

§5. Бином Ньютона

Теорема 5. .

Доказательство. Утверждение доказывается индукцией по n. При имеем , т.е. утверждение выполнено.

Пусть утверждение выполнено для любого . Имеем по предложению индукции.

Тогда (в первой обобщенной сумме выделим последнее слагаемое, а во второй – первое, получим) =

(после замены k на в последнем слагаемом получим) =

(в последнем слагаемом заменим i на k, объединим слагаемые) =

(воспользовались свойством 2 для сочетаний)

(наконец, после замены k на получаем) =. Теорема доказана.

Следствие 1. .

Следствие 2. .

Утверждение следует из теоремы при условии, что .

Следствие 3. .

Утверждение следует из теоремы при условии, что .

Следствие 4. .