
- •Раздел 2. Устойчивость макроскопических систем к флуктуациям в равновесном состоянии, процессы релаксации, фазовые переходы и критические явления.
- •2. 1. Термодинамические условия устойчивости систем к флуктуациям
- •2. 2.Термодинамическое описание релаксационных процессов.
- •2.3. Потеря устойчивости макроскопических систем при отклонениях от равновесного состояния, фазовые переходы и критические явления.
Раздел 2. Устойчивость макроскопических систем к флуктуациям в равновесном состоянии, процессы релаксации, фазовые переходы и критические явления.
2. 1. Термодинамические условия устойчивости систем к флуктуациям
В
классической равновесной термодинамике
проблема стабильности макроскопических
материальных систем при постоянном
составе, температуре и давлении или
объеме
в равновесном состоянии,
за исключением химического равновесия,
сводится к проблеме стабильности
однородной (гомогенной) фазы, т.е. каким
условиям должна удовлетворять гомогенная
система, чтобы она не стала гетерогенной
(не распалась на две отличные от
первоначальной макроскопической) фазы
в результате внешних или внутренних
(локальных, микроскопических) возмущений
(флуктуаций). Наиболее
общий критерий стабильности такой фазы
предложил Гиббс:
если
энергетическое выражение фундаментального
термодинамического уравнения в
интегральной форме
![]() при
определенных значениях интенсивных
параметров Т, р,
при
определенных значениях интенсивных
параметров Т, р,
![]() для какой-либо фазы равно нулю, а для
любой другой фазы, образованной из тех
же компонентов, при тех же условиях
будет больше нуля, то рассматриваемая
фаза по отношению к распаду на другие
фазы является абсолютно стабильной.
для какой-либо фазы равно нулю, а для
любой другой фазы, образованной из тех
же компонентов, при тех же условиях
будет больше нуля, то рассматриваемая
фаза по отношению к распаду на другие
фазы является абсолютно стабильной.
На основе этого критерия и в соответствие с принципом Ле Шателье (если на систему, находящуюся в равновесии, оказывать какое-либо воздействие, отклоняющее от равновесия, то в системе будут протекать процессы, уменьшающее это воздействие) Гиббсом и Дюгемом была разработана классическая термодинамическая (энергетическая) теория устойчивости равновесных состояний к случайным локальным возмущениям (флуктуациям) термодинамических параметров состояния - независимых переменных: температуры (δТ), объема (δV), состава (δNk) или давления (δр), т.е. случайными отклонениями этих величин от значений, соответствующих нормальному, наиболее вероятному (максвелловскому) распределению частиц, образующих систему, по энергиям, т.е. от их средних равновесных (наиболее вероятных) значений. При энергетическом подходе в термодинамике теория устойчивости равновесных состояний к флуктуациям термодинамических параметров базируется на постулате о возрастании термодинамического потенциала (свободной энергии) при возникновении флуктуаций относительно его минимального значения. Соответственно, в системе возникают самопроизвольные (спонтанные) необратимые процессы, ослабляющие этот эффект (принцип Ле Шателье), т.е. уменьшающие свободную энергию за счет положительного приращения энтропии (ΔiF=ΔU-TΔiS<0 или ΔiG=ΔH-TΔiS<0), сохраняя систему в равновесном состоянии. Таким образом, условием стабильности равновесного состояния является то, что возникновение флуктуаций, являясь энергетически невыгодным процессом, сопровождается увеличением термодинамических потенциалов (ΔфF>0 и ΔфG>0), что вызывает самопроизвольное возникновение необратимых процессов, уменьшающих эти потенциалы. Если возникновение и рост флуктуаций станет энергетически выгодным (ΔфF<0 и ΔфG<0), то флуктуации должны самопроизвольно расти, система становится неустойчивой и должна перейти в новое состояние.
Для
оценки изменения термодинамического
потенциала (в общем случае Ψ)
вследствие возникновения флуктуаций
термодинамических параметров (ΔфΨ)
оно разлагается в степенной ряд Тейлора
по вариациям изменения: ΔфΨ=δΨ+![]() +
…(71),
в котором член первого порядка малости
δΨ
является функцией первой степени
флуктуаций температуры (δТ),
объема (δV),
состава (δNk),
а член второго порядка малости
+
…(71),
в котором член первого порядка малости
δΨ
является функцией первой степени
флуктуаций температуры (δТ),
объема (δV),
состава (δNk),
а член второго порядка малости
![]() - функцией второй степени этих флуктуаций,
т.е. (δТ)2,
(δV)2
и (δNk)2
и т.д. Основной вклад в изменение
термодинамических потенциалов вследствие
возникновения флуктуаций вносят члены
второго порядка малости, поэтому условием
устойчивости равновесного состояния
является положительное значение этого
члена ряда
- функцией второй степени этих флуктуаций,
т.е. (δТ)2,
(δV)2
и (δNk)2
и т.д. Основной вклад в изменение
термодинамических потенциалов вследствие
возникновения флуктуаций вносят члены
второго порядка малости, поэтому условием
устойчивости равновесного состояния
является положительное значение этого
члена ряда
![]() или, соответственно, для свободных
энергий Гельмгольца:
или, соответственно, для свободных
энергий Гельмгольца:
![]() и Гиббса:
и Гиббса:![]() .
.
При использовании энтропийной формы фундаментального уравнения применительно к изолированным системам предполагается, что флуктуации термодинамических параметров уменьшают энтропию относительно ее максимального значения (ΔфS<0). Возникающие в системе самопроизвольные (спонтанные) необратимые процессы ослабляют это воздействие в соответствие с принципом Ле Шателье, т.е. увеличивают энтропию за счет ее положительного приращения (ΔiS>0) до максимального значения, сохраняя равновесное состояние. Поэтому условием стабильности равновесного состояния изолированных систем является термодинамичнеская невыгодность возникновения и роста флуктуаций, т.е. уменьшение вследствие этих процессов энтропии (ΔфS<0). Если возникновение и рост флуктуаций является или становится термодинамически выгодным (ΔфS>0), то они должны самопроизвольно расти, и система теряет устойчивость к ним.
Уменьшение
энтропии, вызываемое флуктуациями
термодинамических параметров, также
как увеличение термодинамических
потенциалов при этом, разлагается в
степенной ряд Тейлора по вариациям:
ΔфS=δS+![]() +
…(72),
причем
членами ряда более высокого порядка
малости, чем 2, обычно пренебрегают. В
данном разложении член первого порядка
малости δS
является функцией первой степени
флуктуаций температуры (δТ),
объема (δV)
или состава (δNk),
а член второго порядка малости
+
…(72),
причем
членами ряда более высокого порядка
малости, чем 2, обычно пренебрегают. В
данном разложении член первого порядка
малости δS
является функцией первой степени
флуктуаций температуры (δТ),
объема (δV)
или состава (δNk),
а член второго порядка малости
![]() - функцией второй степени этих флуктуаций,
т.е. (δТ)2,
(δV)2
и (δNk)2,
причем δS
=0, и основной вклад в изменение энтропии
вследствие возникновения флуктуаций
вносит второй член разложения, т.е.
- функцией второй степени этих флуктуаций,
т.е. (δТ)2,
(δV)2
и (δNk)2,
причем δS
=0, и основной вклад в изменение энтропии
вследствие возникновения флуктуаций
вносит второй член разложения, т.е.
![]() =
=![]() .
При
этом условием устойчивости системы к
флуктуациям термодинамических параметров
является отрицательное значение этого
члена ряда:
.
При
этом условием устойчивости системы к
флуктуациям термодинамических параметров
является отрицательное значение этого
члена ряда:
![]() <0.
<0.
Термодинамические расчеты вариаций энтропии вследствие флуктуаций температуры, объема и состава (числа молей компонентов) в изолированной системе в равновесном состоянии были проведены Гиббсом и Дюгемом в предположении, что флуктуация происходит в малой (локальной) части (обозначается индексом 1) макроскопической системы, основная часть которой обозначается индексом 2, и не нарушает общее состояние системы:
-
Локальная флуктуация внутренней энергии заключается в ее изменениях для частей системы 1 и 2 при сохранении неизменной общей энергии системы (δU1=-δU2=δU). При этом значения первой и второй вариации энтропии равны:
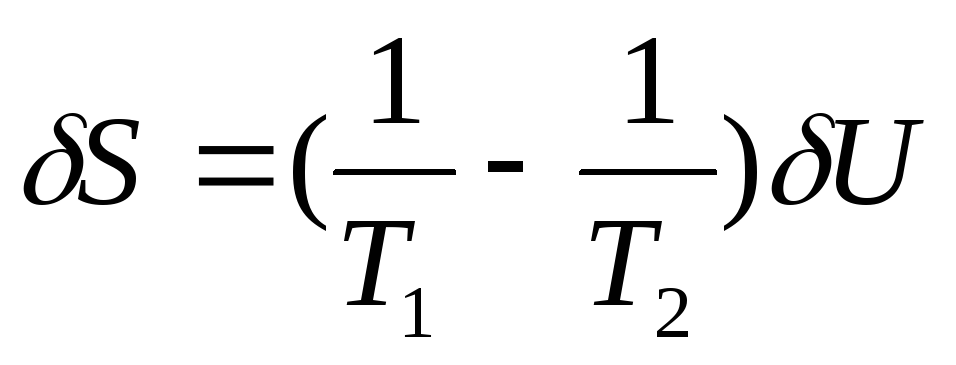 (73)
и
(73)
и
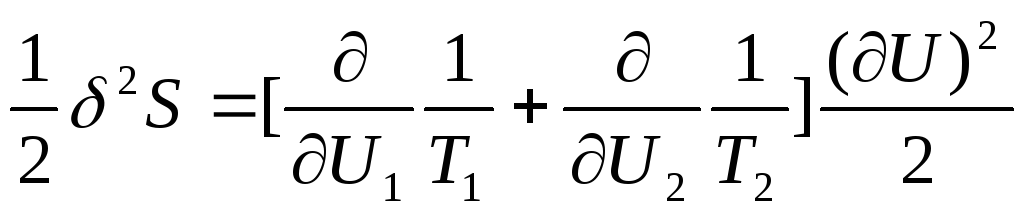 (74).
В равновесии термодинамические силы
и потоки отсутствуют, и температура в
обеих частях системы одинакова, т.е.
Т1=Т2
. Следовательно, первая вариация энтропии
δS=0.
В формуле для второй вариации
(74).
В равновесии термодинамические силы
и потоки отсутствуют, и температура в
обеих частях системы одинакова, т.е.
Т1=Т2
. Следовательно, первая вариация энтропии
δS=0.
В формуле для второй вариации
 (75),
где
(75),
где
 - мольная
теплоемкость. Подставляя уравнение
(75
)
в
(74),
получаем:
- мольная
теплоемкость. Подставляя уравнение
(75
)
в
(74),
получаем:
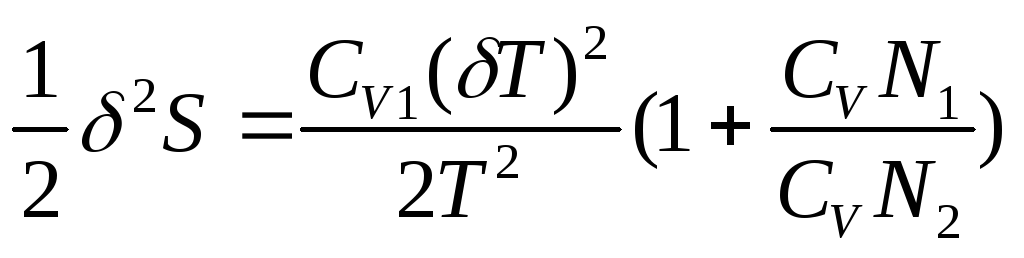 (76
),
где δТ
- изменение температуры (тепловая
флуктуация) в
малой части системы. Так как часть 1
системы мала по сравнению с основной
частью 2 (
(76
),
где δТ
- изменение температуры (тепловая
флуктуация) в
малой части системы. Так как часть 1
системы мала по сравнению с основной
частью 2 ( N1<<
N1<<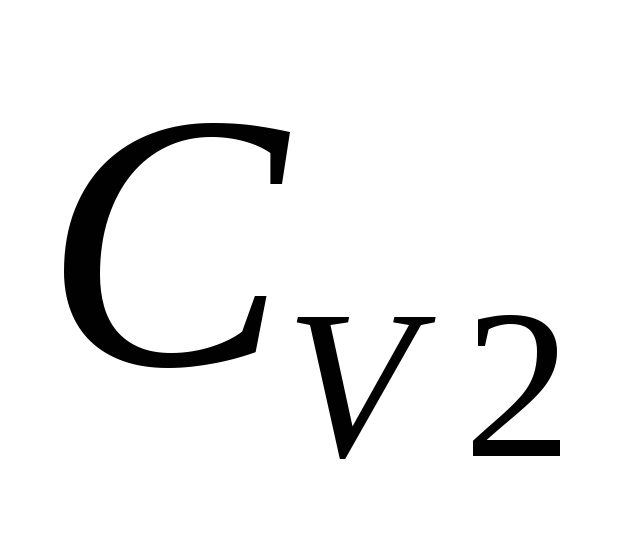 N2),
то
N2),
то
 (77
).
Таким образом, условием устойчивости
системы к тепловым флуктуациям
(тепловой
устойчивости) и равновесного состояния
является ΔфS=
(77
).
Таким образом, условием устойчивости
системы к тепловым флуктуациям
(тепловой
устойчивости) и равновесного состояния
является ΔфS=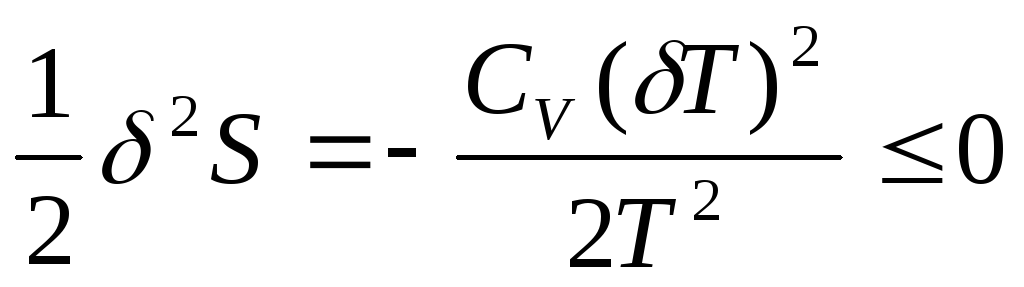 ,
причем эти условия соблюдаются только
при положительном значении теплоемкости
системы, т.е.при
,
причем эти условия соблюдаются только
при положительном значении теплоемкости
системы, т.е.при
 >0.
>0.
-
Локальная флуктуация объема заключается в изменениях объема частей системы 1 и 2 при сохранении неизменным общего объема, т.е. δV1=-δV2=δV. Аналогично предыдущему cлучаю значения первой и второй вариации энтропии равны:
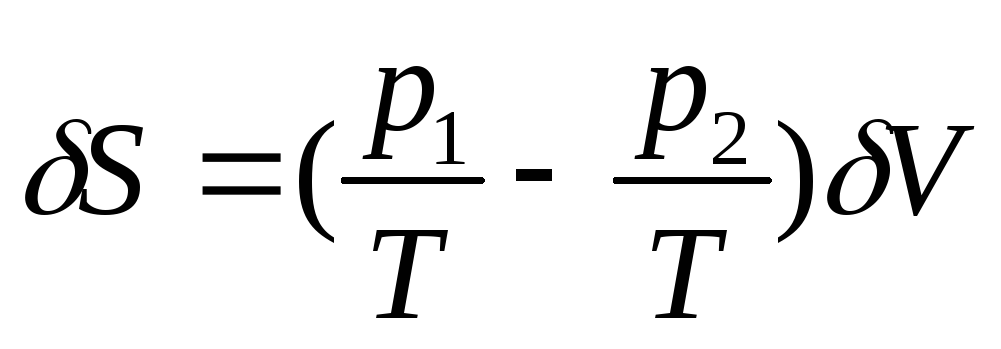 (78)
и
(78)
и
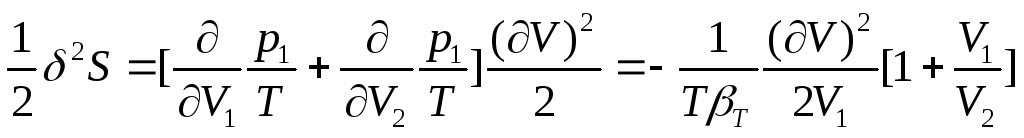 <0
(79),
где
<0
(79),
где
 - изотермическая объемная сжимаемость
- изотермическая объемная сжимаемость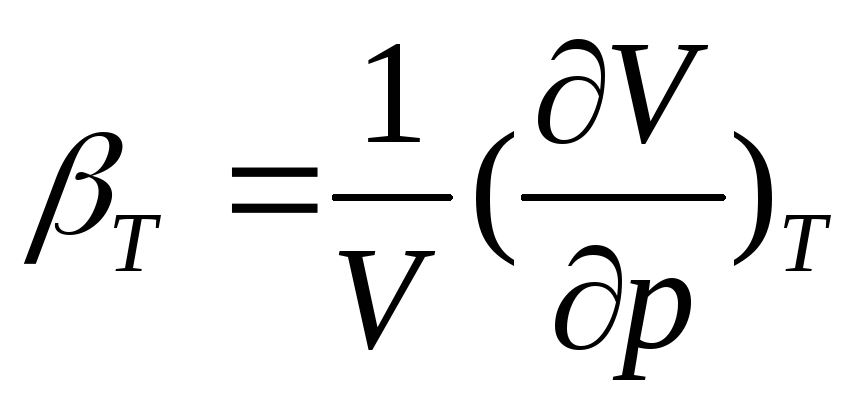 .
Так как в равновесии
.
Так как в равновесии
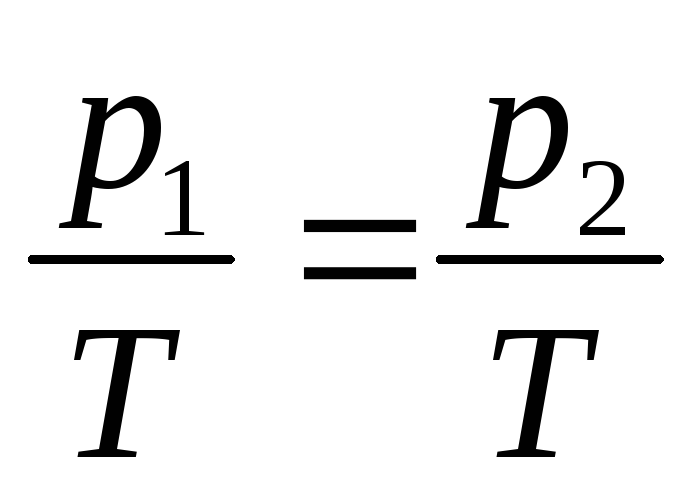 ,
то δS=0,
а так как V1<<
V2,
то
,
то δS=0,
а так как V1<<
V2,
то
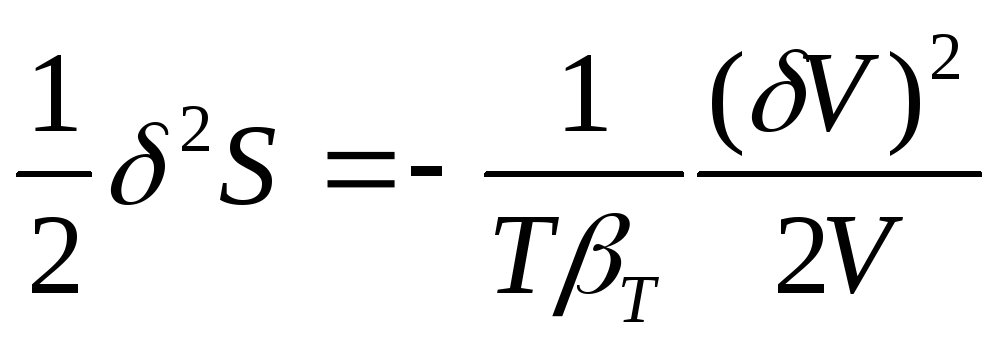 (80).
Таким образом, условием устойчивости
системы к флуктуациям объема или
плотности (механической устойчивости)
и равновесного состояния является
(80).
Таким образом, условием устойчивости
системы к флуктуациям объема или
плотности (механической устойчивости)
и равновесного состояния является
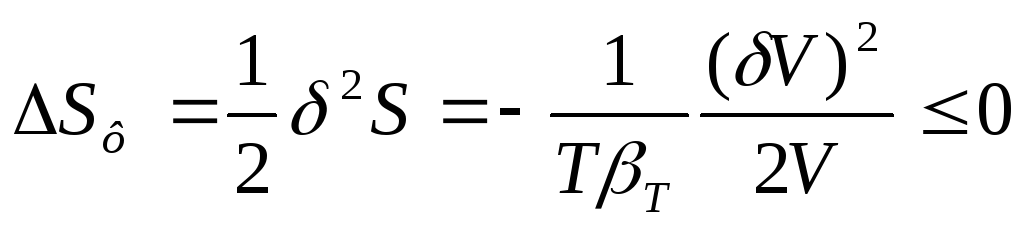 ,
причем эти условия обеспечиваются
только при положительном значении
объемной сжимаемости (
,
причем эти условия обеспечиваются
только при положительном значении
объемной сжимаемости (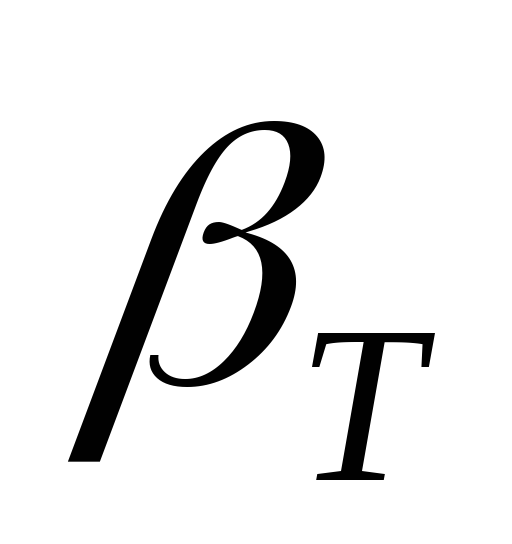 >0).
>0). -
Локальная флуктуация числа молей компонентов в многокомпонентной системе, обусловленная диффузионным обменом молекулами межу частями 1 и 2 (δNk1=-δNk2=δNk) при сохранении неизменным их общего количества, определяет следующим образом значения первой и второй вариации энтропии:
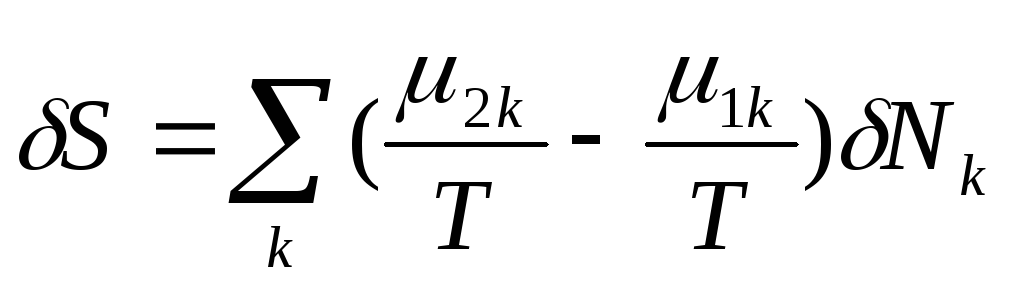 (81)
и
(81)
и
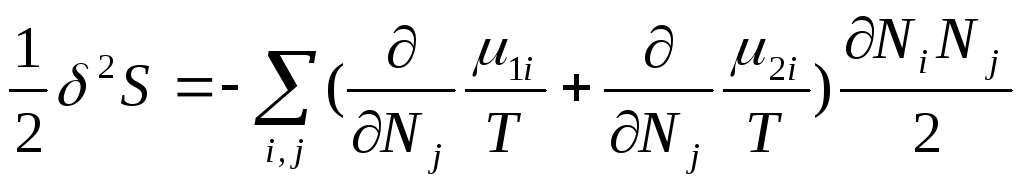 (82).
В равновесном состоянии
(82).
В равновесном состоянии
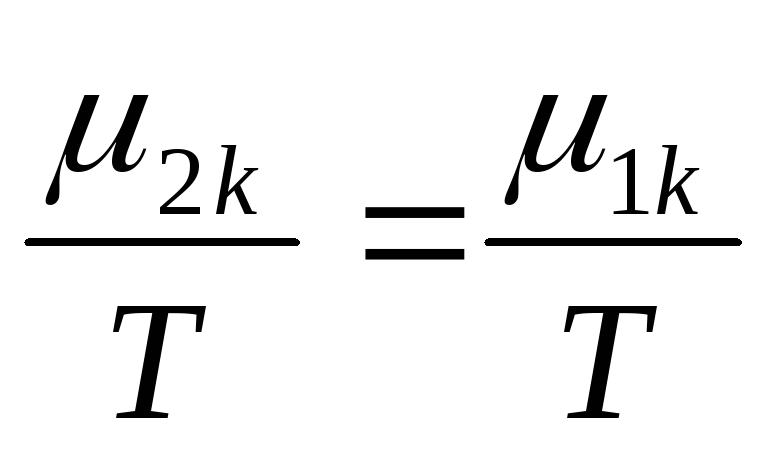 ,
следовательно δS=0,
а так как часть системы 1 намного меньше
части 2, то
,
следовательно δS=0,
а так как часть системы 1 намного меньше
части 2, то
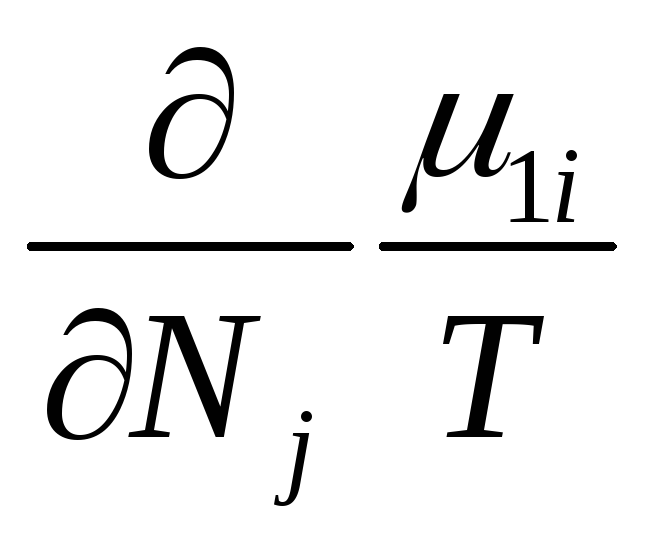 >>
>>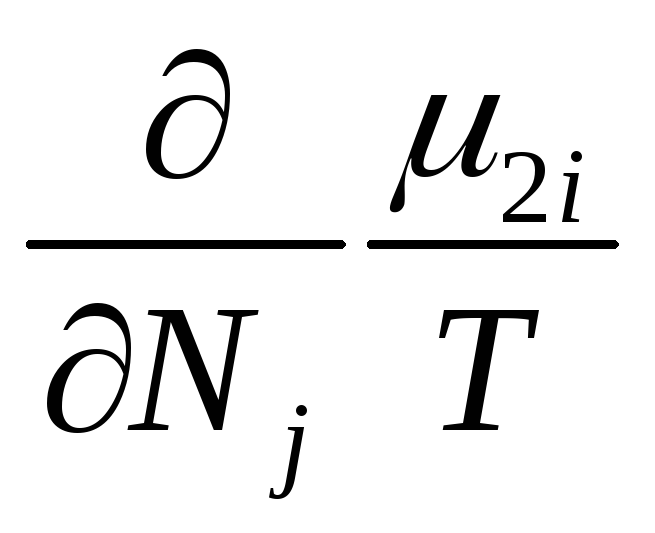 и
и
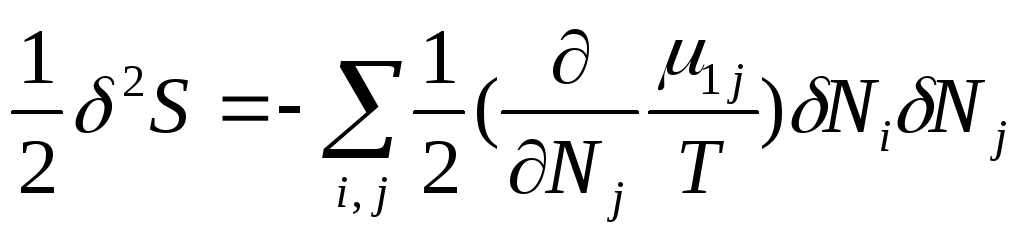 (83).
Таким образом, условием устойчивости
системы к флуктуациям концентрации и
равновесного состояния является
(83).
Таким образом, условием устойчивости
системы к флуктуациям концентрации и
равновесного состояния является ,
причем эти условия обеспечиваются
только при положительном значении
химического потенциала (
,
причем эти условия обеспечиваются
только при положительном значении
химического потенциала (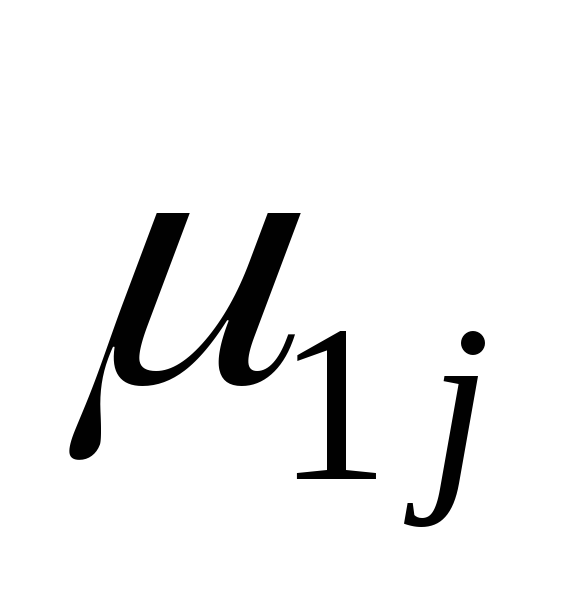 >0).
Эти условия могут быть также применено
к устойчивости химического равновесия
к флуктуациям степени превращения δξ
в химических реакциях в предположении,
что δNk=υkδξ,
где υk
– стехиометрический коэффициент. Тогда
>0).
Эти условия могут быть также применено
к устойчивости химического равновесия
к флуктуациям степени превращения δξ
в химических реакциях в предположении,
что δNk=υkδξ,
где υk
– стехиометрический коэффициент. Тогда
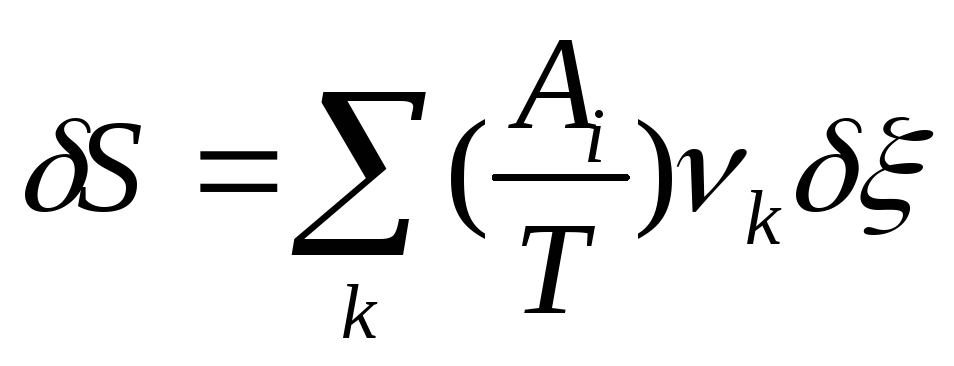 и
и
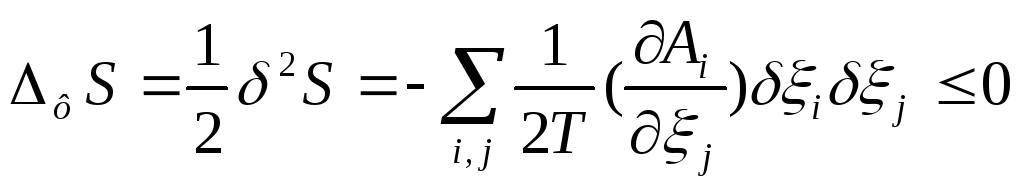 (84).
(84).
Таким
образом, при флуктуациях основных
термодинамических независимых переменных
(δТ,
δV
и δNk)
общее изменение энтропии при возникновении
флуктуаций температуры, плотности и
концентрации или химического превращения
и условие устойчивости к ним равновесного
состояния может быть выражено обобщенным
уравнением:
![]() =
=![]() <0
(85).
В этом выражении
<0
(85).
В этом выражении
![]() ,
,
![]() и
и
![]() .
Тогда уравнение (85)
можно записать через произведение
парных переменных:
.
Тогда уравнение (85)
можно записать через произведение
парных переменных:
![]() (86).
(86).
Обобщенная
термодинамическая теория флуктуаций,
развитая Эйнштейном,
позволяет рассчитывать по величине
![]() вероятности флуктуаций термодинамических
параметров в равновесном состоянии.
Как хорошо известно, впервые идею
вероятности в термодинамику ввел
Больцман, который предположил, что
энтропия любой макроскопической системы
равна:
вероятности флуктуаций термодинамических
параметров в равновесном состоянии.
Как хорошо известно, впервые идею
вероятности в термодинамику ввел
Больцман, который предположил, что
энтропия любой макроскопической системы
равна:
![]() (87),
где
(87),
где
![]() - вероятность
- вероятность
![]() состояния в множестве дискретных
состояний при i=1,2,
…,w.
При равновероятном состоянии всех
состояния в множестве дискретных
состояний при i=1,2,
…,w.
При равновероятном состоянии всех
![]() состояний, т.е при Р1=Р2=….=Рi=1/w
выражение (87)
дает известное соотношение Больцмана:
состояний, т.е при Р1=Р2=….=Рi=1/w
выражение (87)
дает известное соотношение Больцмана:![]() ,
где w
– число микросостояний, соответствующих
макросостоянию системы, энтропия которой
равна
,
где w
– число микросостояний, соответствующих
макросостоянию системы, энтропия которой
равна
![]() .
Это число по предложению Макса Планка
иногда называют термодинамической
вероятностью,
которая, в отличие от обычной вероятности,
значительно больше единицы.
.
Это число по предложению Макса Планка
иногда называют термодинамической
вероятностью,
которая, в отличие от обычной вероятности,
значительно больше единицы.
Эйнштейн,
в противоположность Больцману,
применившему термодинамическую
вероятность для вывода энтропии,
наоборот, использовал энтропию для
вывода вероятности термодинамических
флуктуаций:
![]() (88),
где Z
– нормировочный множитель, обеспечивающий
равенство суммы всех вероятностей
(88),
где Z
– нормировочный множитель, обеспечивающий
равенство суммы всех вероятностей
![]() единице, а
единице, а
![]() -
изменение энтропии вследствие
возникновения флуктуации независимых
термодинамических параметров. Подстановка
в формулу Эйнштейна (88)
значения
-
изменение энтропии вследствие
возникновения флуктуации независимых
термодинамических параметров. Подстановка
в формулу Эйнштейна (88)
значения
![]() в соответствие с уравнением (85)
дает общее выражение для вероятности
флуктуаций δТ,
δV
и δNk:
в соответствие с уравнением (85)
дает общее выражение для вероятности
флуктуаций δТ,
δV
и δNk:
![]() (89).
В более простом виде с учетом соотношения
(86)
это выражение может быть записано через
произведение парных переменных:
(89).
В более простом виде с учетом соотношения
(86)
это выражение может быть записано через
произведение парных переменных:
![]() (90).
(90).
Нормировочный
множитель определяется как
![]() ,
а распределение вероятности принимается
гауссовым для каждой независимой
переменной
δТ,
δV
и δNk.
Использование этих представлений и
приведенных соотношений позволяет
определить вероятность флуктуаций в
явном виде и рассчитать их среднеквадратичные
значения.
,
а распределение вероятности принимается
гауссовым для каждой независимой
переменной
δТ,
δV
и δNk.
Использование этих представлений и
приведенных соотношений позволяет
определить вероятность флуктуаций в
явном виде и рассчитать их среднеквадратичные
значения.
При
обобщенной записи уравнения (90)
для любого набора независимых
термодинамических параметров Хk,
флуктуации которых от равновесного
значения обозначаются как δХk,
и заменяют переменные
δТ,
δV
и δNk,
изменение энтропии за счет этой флуктуации
есть квадратичная функция δХk:
![]() (90),
где
(90),
где
![]() -
коэффициент пропорциональности, а
-
коэффициент пропорциональности, а
![]() -
термодинамическая сила. Например, для
изменения энтропии, вызванного
флуктуациями степени превращения в r
химических реакциях (см. уравнение 84)
-
термодинамическая сила. Например, для
изменения энтропии, вызванного
флуктуациями степени превращения в r
химических реакциях (см. уравнение 84)
![]() ,
а
,
а
![]() .
При наличии распределения вероятности
для набора переменных δХk
эти соотношения позволяют определять
средние значения любой функции этих
переменных и корреляции между парами
переменных. Установлено, что каждая
флуктуация коррелирует только с
соответствующей и ни с какой другой
термодинамической силой. Среднее
значение флуктуаций энтропии для m
независимых переменных δХk
равна:
.
При наличии распределения вероятности
для набора переменных δХk
эти соотношения позволяют определять
средние значения любой функции этих
переменных и корреляции между парами
переменных. Установлено, что каждая
флуктуация коррелирует только с
соответствующей и ни с какой другой
термодинамической силой. Среднее
значение флуктуаций энтропии для m
независимых переменных δХk
равна:
![]() ,
где k
–константа
Больцмана, т.е. каждый
независимый процесс вносит вклад в
изменение энтропии, обусловленное
флуктуациями термодинамических
параметров, равный –k/2,
причем знак минус показывает, что
флуктуации уменьшают энтропию.
Этот результат аналогичен теореме
статистической механики, согласно
которой каждая степень свободы теплового
движения дает вклад в увеличение средней
энергии, равный kТ/2.
С помощью этих соотношений получен
простой вывод соотношений взаимности
Онсагера.
,
где k
–константа
Больцмана, т.е. каждый
независимый процесс вносит вклад в
изменение энтропии, обусловленное
флуктуациями термодинамических
параметров, равный –k/2,
причем знак минус показывает, что
флуктуации уменьшают энтропию.
Этот результат аналогичен теореме
статистической механики, согласно
которой каждая степень свободы теплового
движения дает вклад в увеличение средней
энергии, равный kТ/2.
С помощью этих соотношений получен
простой вывод соотношений взаимности
Онсагера.
