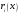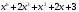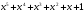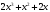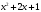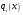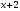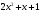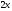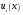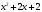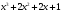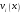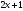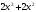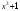- •Лекція № 8 Тема: Многочлени над скінченними полями
- •1. Кільце многочленів над скінченним полем
- •2. Операції в кільці многочленів над скінченним полем.
- •3. Конгруентність многочленів над скінченним полем
- •4. Незвідні многочлени над скінченним полем
- •Властивості незвідних многочленів над полем :
- •5. Скінченні поля на базі кілець многочленів
- •6. Примітивні многочлени
- •7. Побудова скінченного поля
Ю.Д.Жданова. Лекції з МОКП. М3 Скінченні поля. Лекція № 8
Лекція № 8 Тема: Многочлени над скінченними полями
План лекції:
-
Кільце многочленів над скінченним полем.
-
Операції в кільці многочленів над скінченним полем.
-
Конгруентність многочленів над скінченним полем.
-
Незвідні многочлени над скінченним полем.
-
Скінченні поля на базі кілець многочленів.
-
Примітивні многочлени.
1. Кільце многочленів над скінченним полем
Скінченні
поля на базі кілець класів
лишків
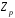 за даним простим модулем – не єдиний
приклад скінченних полів. Розберемо ще
один приклад скінченних полів, який
являє собою інтерес для криптографії.
за даним простим модулем – не єдиний
приклад скінченних полів. Розберемо ще
один приклад скінченних полів, який
являє собою інтерес для криптографії.
Означення.
Нехай
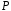 – підполе поля
– підполе поля
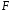 і
і
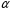 – деякий елемент поля
– деякий елемент поля
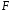 .
Мінімальне поле, яке містить поле
.
Мінімальне поле, яке містить поле
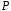 і елемент
і елемент
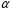 ,
називається простим
розширенням поля
,
називається простим
розширенням поля
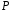 ,
яке отримане приєднанням до поля
,
яке отримане приєднанням до поля
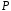 елементу
елементу
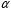 .
Це розширення позначається через
.
Це розширення позначається через
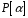 .
.
Приклад.
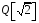 – просте розширення поля раціональних
чисел
– просте розширення поля раціональних
чисел
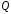 .
.
Поняття розширення поля дозволяє вводити і використовувати велику різноманітність кілець, елементи яких визначаються як многочлени
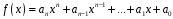
з
коефіцієнтами
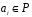 .
Такі многочлени називаються многочленами
над полем
.
Такі многочлени називаються многочленами
над полем
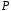 .
Найбільше число
.
Найбільше число
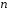 таке, що коефіцієнт
таке, що коефіцієнт
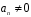 називається степенем многочлена
називається степенем многочлена
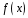 і позначається
і позначається
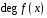 .
Якщо при цьому
.
Якщо при цьому
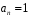 ,
то многочлен називається нормованим.
,
то многочлен називається нормованим.
Множина
всіх многочленів над полем
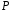 утворює кільце
утворює кільце
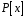 .
Операції
додавання і множення кільця
.
Операції
додавання і множення кільця
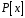 визначаються тими ж правилами, за якими
додаються або перемножуються многочлени
над полем дійсних чисел
визначаються тими ж правилами, за якими
додаються або перемножуються многочлени
над полем дійсних чисел
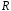 .
Нулем кільця многочленів є многочлен
0, усі коефіцієнти якого дорівнюють 0.
.
Нулем кільця многочленів є многочлен
0, усі коефіцієнти якого дорівнюють 0.
Відзначимо,
що многочлени
над полем утворюють саме кільце, а не
поле,
тому що не існує таких
многочленів
степеня
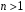 ,
які б при множенні давали б одиницю:
,
які б при множенні давали б одиницю:
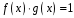 ,
тобто в кільці многочленів для кожного
елемента, що не є ненульовим сталим
многочленом, відсутній обернений
елемент.
,
тобто в кільці многочленів для кожного
елемента, що не є ненульовим сталим
многочленом, відсутній обернений
елемент.
Означення.
Многочленом
степеня
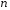 над
скінченним полем
від
однієї змінної називається
вираз вигляду:
над
скінченним полем
від
однієї змінної називається
вираз вигляду:
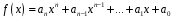 ,
,
де
коефіцієнти многочлена
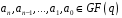 .
.
Приклад
1.
Для
многочлена над полем
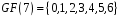 можна
записати
можна
записати
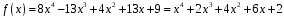 .
.
Многочлени
над скінченним полем
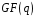 відносно звичайних операцій додавання
і множення утворюють кільце, яке
називається кільцем
многочленів над полем
відносно звичайних операцій додавання
і множення утворюють кільце, яке
називається кільцем
многочленів над полем
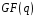 і позначається
і позначається
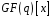 .
.
2. Операції в кільці многочленів над скінченним полем.
Для кільця многочленів над скінченним полем справедливі операції додавання, множення, ділення з остачею. Крім того, має місце відношення конгруентності.
Приклад
2.
Знайти суму і добуток многочленів
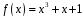 і
і
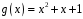 над полем
над полем
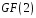 .
.
Розв’язання.
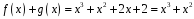 ;
;
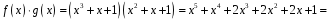
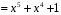 .
.
Означення.
Якщо
для многочленів
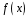 і
і
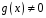 в кільці
в кільці
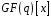 існують
такі многочлени
існують
такі многочлени
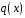 і
і
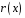 ,
що многочлен
,
що многочлен
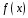 можна подати у вигляді
можна подати у вигляді
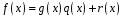
де
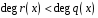 ,
то кажуть, що многочлен
,
то кажуть, що многочлен
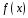 ділиться на
многочлен
ділиться на
многочлен
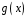 з остачею.
з остачею.
Приклад
3.
Поділити
многочлен
 на многочлен
на многочлен
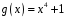 з остачею над полем
з остачею над полем
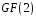 .
.
Розв’язання. Ділення відбувається кутом, на кожному проміжному етапі обчислень результат зводиться за модулем 2 (підкреслено подвійною рискою)
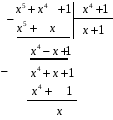
Отже,
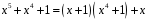 .
.
Приклад
4.
Поділити
многочлен
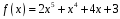 на многочлен
на многочлен
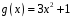 з остачею над полем
з остачею над полем
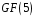 .
.
Розв’язання. Ділення відбувається кутом, на кожному проміжному етапі обчислень результат зводиться за модулем 5 (підкреслено подвійною рискою)
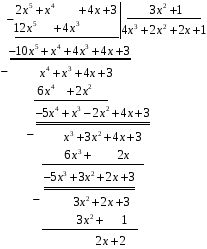
Отже,
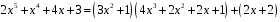 .
.
У
кільці
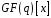 зберігаються означення та властивості
найбільшого спільного дільника
многочленів, зокрема діє алгоритм
Евкліда для визначення НСД і розширений
алгоритм Евкліда для визначення лінійного
представлення НСД.
зберігаються означення та властивості
найбільшого спільного дільника
многочленів, зокрема діє алгоритм
Евкліда для визначення НСД і розширений
алгоритм Евкліда для визначення лінійного
представлення НСД.
Приклад 5. Знайти
а)
НСД многочленів
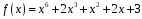 і
і
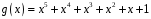 над полем
над полем
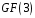 ;
;
б)
лінійне представлення НСД многочленів
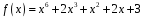 і
і
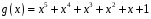 над полем
над полем
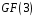 .
.
Розв’язання.
а) Дотримуючись
алгоритму Евкліда, поділимо многочлен
 на
многочлен
на
многочлен
 ,
на
кожному проміжному етапі обчислень
результат зводиться за модулем 3:
,
на
кожному проміжному етапі обчислень
результат зводиться за модулем 3:

Поділимо
многочлен
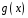 на многочлен
на многочлен
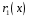 :
:

Поділимо
многочлен
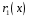 на многочлен
на многочлен
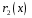 :
:
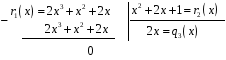
Отже,
 .
.
б)
За
допомогою розширеного алгоритму Евкліда
знайдемо лінійне представлення
найбільшого спільного дільника
многочленів
 і
і
 над полем
над полем
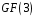 .
.
Протокол роботи розширеного алгоритму Евкліда оформимо у вигляді таблиці:
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
0 |
1 |
|
|
|
Таким
чином, над
полем
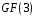
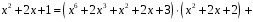 .
.
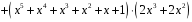 .
.