2. Основные уравнения и формулы
2.1. Волновые свойства света
Скорость света в среде
,
где
– скорость света в вакууме;
– абсолютный показатель преломления
среды.
Оптическая длина пути световой волны
,
где
– геометрическая длина пути световой
волны в среде с показателем преломления
.
Оптическая разность хода двух световых волн
.
Оптическая разность хода световых волн, отражённых от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или плёнки, находящейся в воздухе,
или
,
где
– толщина пластинки (плёнки);
– угол падения;
– угол преломления;
– длина световой волны в вакууме.
Второе слагаемое
в этих формулах учитывает изменение
оптической длины пути световой волны
на
при отражении её от среды оптически
более плотной.
В проходящем свете отражение световой волны происходит от среды оптически менее плотной, и дополнительной разности хода световых лучей не возникает.
Связь разности
фаз
колебаний с оптической разностью хода
волн
.
Условие максимумов интенсивности света при интерференции:
(
=0,
1, 2, 3, …).
Условие минимумов интенсивности света при интерференции:
.
Радиусы светлых колец Ньютона в отражённом свете (или тёмных в проходящем)
,
где
– номер кольца (
= 1, 2, 3, …);
– радиус кривизны поверхности линзы,
соприкасающейся с плоскопараллельной
стеклянной пластинкой.
Радиусы тёмных колец в отражённом свете (или светлых в проходящем)
.
Радиус
-й
зоны Френеля:
-
для сферической волны
,
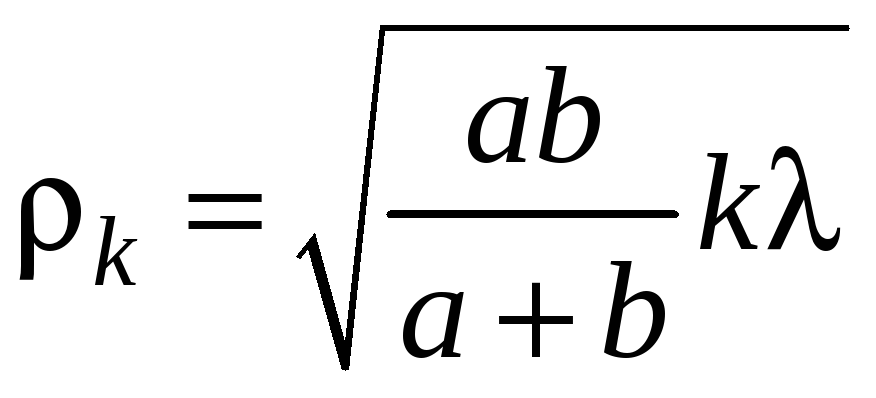где
– расстояние от диафрагмы с круглым
отверстием до точечного источника
света;
– расстояние от диафрагмы до экрана;
– номер зоны Френеля;
– длина волны;
-
для плоской волны
.
Дифракция света на одной щели при нормальном падении лучей
Условие максимумов интенсивности света:
;
=1,
2, 3, …,
где
– ширина щели;
– угол дифракции;
– номер минимума;
– длина волны.
Условие минимумов интенсивности света:
;
=1,
2, 3, …
Дифракция света на дифракционной решётке при нормальном падении лучей
Условие главных максимумов интенсивности:
=0,
1, 2, …,
где
– период (постоянная) решётки;
– номер главного максимума;
– угол между нормалью к поверхности
решётки и направлением дифрагированных
волн.
Разрешающая сила дифракционной решётки
,
где
– наименьшая разность длин волн двух
соседних спектральных линий (
и
),
при которой эти линии могут быть видны
раздельно в спектре, полученном
посредством данной решётки;
– число штрихов решётки;
– порядковый номер дифракционного
максимума.
Угловая дисперсия дифракционной решётки
.
Линейная дисперсия дифракционной решётки
;
для малых углов дифракции
,
где F– главное фокусное расстояние линзы, собирающей на экране дифрагирующие волны.
Формула Вульфа – Брэгга:
,
где
– расстояние между атомными плоскостями
кристалла;
– угол скольжения.
Закон Брюстера:
,
где
– угол падения, при котором отражённая
световая волна полностью поляризована;
– относительный показатель преломления.
Закон Малюса:
,
где
– интенсивность плоскополяризованного
света, прошедшего через анализатор;
– интенсивность плоскополяризованного
света, падающего на анализатор;
– угол между направлением колебаний
светового вектора волны, падающей на
анализатор, и плоскостью пропускания
анализатора.
Степень поляризации света
,
где
и
– максимальная и минимальная интенсивность
частично поляризованного света,
пропускаемого анализатором.
Угол поворота
плоскости
поляризации оптически активными
веществами определяется соотношениями:
-
в твёрдых телах
,
где
– постоянная вращения;
– длина пути, пройденного светом в
оптически активном веществе; -
в чистых жидкостях
,
где
– удельное вращение;
– плотность жидкости; -
в растворах
,
где
– массовая концентрация оптически
активного вещества в растворе.