33. Кореляційний аналіз

Кореляційний аналіз є одним із широко розповсюджених методів оцінки статистичних зв'язків. Він відповідає на питання: чи впливає вхідна величина на вихідну і яка ступінь (тіснота) зв'язку між величинами? Ступінь зв'язку оцінюється коефіцієнтом кореляції.

Якщо оцінюється вплив на вихідну однієї вхідної величини, то визначається коефіцієнт парної кореляції.

У кореляційному аналізі виходять із того, що як вхідні, так і вихідні величини є випадковими.

Оцінкою коефіцієнта парної кореляції є величина:

Перевірка значимості коефіцієнта кореляції здійснюється по виразу:

де T_α – табличне значення критерію Стьюдента для f= n-2 і відповідного рівня значимості, величина якого наведена в таблиці.

 

Значення критерію Стьютента для рівня значимості =0,05

 

f	1	2	3	4	5	6	8	10	20	30	60
tα	12,71	4,303	3,182	2,775	2,571	2,447	2,305	2,228	2,086	2,042	2,00

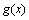34. Апроксимацією (наближенням) функції називається знаходження такої функції (апроксимуючої функції), що була б близька заданої. Критерії близькості функцій і можуть бути різні.

У тому випадку, коли наближення будується на дискретному наборі точок, апроксимацію називають точковою або дискретною.

У тому випадку, коли апроксимація проводиться на безперервній множині точок (відрізку), апроксимація називається безперервною або інтегральню.

35. Лінійна інтерполяція.

Найпростішим випадком локальної інтерполяції є лінійна інтерполяція, коли інтерполяційна функція вибирається поліном першого ступеня, тобто вузлові точки з'єднуються прямою лінією. (мал. 1)

Рис. 1

36. Інтерполяція сплайнами

Серед методів локальної інтерполяції найбільше поширення одержала інтерполяція сплайнами (від англійського слова spline – гнучка лінійка). При цьому будується інтерполяційний поліном третього ступеня, що проходить через всі задані вузли й має безперервні першу й другу похідні. На кожному інтервалі функція, що інтерполює, є поліномом третього ступеня 

і задовольняє умовам 

. (1)

Якщо всього n вузлів, то інтервалів – . Виходить, потрібно визначити невідомих коефіцієнтів поліномів. Умова (1) дає нам n рівнянь. Умова безперервності функції і її перших двох похідних у внутрішніх вузлах інтервалу дає додатково рівнянь 

Усього маємо різних рівнянь. Два відсутні рівняння можна одержати, задаючи умови на краях інтервалу. Зокрема, можна зажадати нульової кривизни функції на краях інтервалу, тобто

Задаючи різні умови на кінцях інтервалу, можна одержати різні сплайни. Приклад інтерполяції сплайнами представлений на малюнку 2.

Рис. 2