26. Чисельні методи розв’язання диференціальних рівнянь

Нехай необхідно знайти рішення рівняння

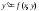(1)

с початковою умовою . Розкладемо шукану функцію в ряд поблизу точки 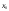й обмежимося першими двома членами розкладання 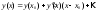. Урахувавши рівняння (1) й позначивши , одержуємо 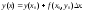Цю формулу можна застосовувати багаторазово, знаходячи значення функції в усі нових і нових точках.

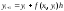(2)

27. Розв’язання диференціальних рівнянь за допомогою функції odesolve в Mathcad

У бібліотеці убудованих функцій Mathcad є функція odesolve, призначена для рішення лінійних диференціальних рівнянь. Функція odesolve вирішує задачу Коші з початковими умовами

або найпростішу крайову задачу, у якій задані n граничних умов, що визначають значення шуканої функції і її похідних у кінцях відрізка , тобто задані n граничних умов виду

, , , .

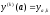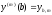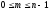Запишіть!

Для рішення диференціальних рівнянь за допомогою функції odesolve необхідно:

1. увести ключове слово Given для використання вирішального блоку;

2. задати диференціальне рівняння і його обмеження, що використовують булеві оператори;

3. увести функцію odesolve (x, b, [step]) зі змінною інтегрування x і кінцевою точкою b.

28. Метод Ейлера для диференціальних рівнянь першого порядку в MathCad

Вирішимо задачу Коші для диференціального рівняння першого порядку 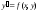методом Ейлера.

Нехай права частина рівняння дорівнює

Задамо границі зміни x:

Задамо число точок і величину кроку:

Задамо початкові умови:

Обчислимо x і y по формулах Ейлера

Представимо результат графічно й порівняємо його з аналітичним рішенням

Точне аналітичне рішення й рішення, отримане чисельно, відрізняються в точці x=1 на

Тобто відносна помилка становить

29. Рішення систем диференціальних рівнянь в Mathcad.

Для рішення диференціальних рівнянь Mathcad має ряд убудованих функцій, зокрема, функцію rkfixed, що реалізує метод Рунге-Кутти четвертого порядку з фіксованим кроком. Фактично ця функція призначена для рішення систем диференціальних рівнянь першого порядку.

Запишіть!

Функція rkfixed(y, x1, x2, npoints, D) повертає матрицю. Перший стовпець цієї матриці містить точки, у яких отримане рішення, а інші стовпці – рішення і його перші похідні.

Аргументи функції:

• y – вектор початкових значень (n елементів).

• x1 і x2 – границі інтервалу, на якому шукається рішення диференціального рівняння.

• npoints – число точок усередині інтервалу (x1,x2), у яких шукається рішення. Функція rkfixed повертає матрицю, що складається з 1+npoints рядків.

• D – вектор, що складається з n елементів, що містить перші похідні шуканої функції.

30. Рішення диференціальних рівнянь методом Рунге-Кутти

Вирішимо ще раз задачу Коші для диференціального рівняння першого порядку методом Рунге-Кутти.

Задамо границі зміни x:

Задамо число крапок усередині інтервалу

Задамо початкові умови . Оскільки ми вирішуємо тільки одне диференціальне рівняння першого порядку, а не систему диференціальних рівнянь, матриця y містить тільки один елемент, однак запис y=1 була б неправильною. Необхідно явно вказувати на те, що величина y – матриця, тобто писати індекс.

Визначимо тепер матрицю похідних. Ця матриця теж складається тільки з одного елемента. Цей елемент із точністю до позначень збігається із правою частиною вихідного диференціального рівняння:

Вирішуємо диференціальне рівняння

Точне аналітичне рішення й рішення, отримане чисельно відрізняються в точці 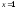на

Відносна помилка становить