
- •Рівномірний розподіл
- •Розподіл « xи-квадрат»
- •Показовий розподіл
- •Математичне очікування
- •Рівняння виду
- •Диференціальні рівняння виду , що не містять шуканої функції
- •Загальний розв’язок лінійного однорідного рівняння з постійними коефіцієнтами
- •Линейные неоднородные уравнения с постоянными коэффициентами. Общее решение. Метод подбора.
- •Чисельні методи розв’язання диференціальних рівнянь
- •Розв’язання диференціальних рівнянь за допомогою функції odesolve в Mathcad
- •Метод Ейлера для диференціальних рівнянь першого порядку в MathCad
- •Рішення систем диференціальних рівнянь в Mathcad.
- •Рішення диференціальних рівнянь методом Рунге-Кутти
- •Розв’язання диференціальних рівнянь вищих порядків
- •Кореляційний аналіз
- •Лінійна інтерполяція.
- •Інтерполяція сплайнами
-
Рівняння виду
Розв’язок
такого рівняння знаходиться
 -кратним
інтегруванням, а саме:
-кратним
інтегруванням, а саме:
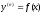 ,
,
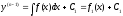 ,
,
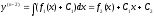 ,
,
…………………………………………………
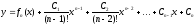 ,
,
де
 .
.
Оскільки
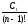 ,
,
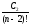 ,
… є сталими величинами, то загальний
розв’язок можебути записаний так:
,
… є сталими величинами, то загальний
розв’язок можебути записаний так:
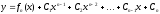 .
.
-
Диференціальні рівняння виду , що не містять шуканої функції
Порядок
такого рівняння можна понизити, прийнявши
за нову невідому функцію, найнижчу із
похідних даного рівняння, тобто вважаючи
 .
Тоді отримаємо рівняння
.
Тоді отримаємо рівняння
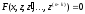 .
.
Таким
чином, порядок рівняння знижується на
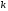 одиниць.
одиниць.
-
Диференціальні рівняння виду
 ,
що однорідні відносно
,
що однорідні відносно
 ,
,
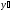 ,
,
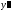 ,
...,
,
...,
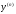
Рівняння
такого типу допускають пониження порядку
похідної при заміні
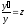 .
.
Розглянемо
приклад.
Розв’яжемо рівняння
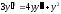 .
.
Розділимо
обидві частини рівняння на
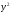 :
:
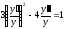 .
.
Запровадимо
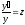 ,
звідки
,
звідки
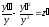 ,
або
,
або
 .
В результаті отримаємо рівняння
.
В результаті отримаємо рівняння
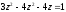 ,
або
,
або
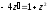 ,
тобто
,
тобто
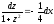 .
.
Звідси, інтегруючи, знаходимо
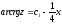 ,
або
,
або
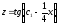 ,
або
,
або
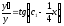 .
.
-
Принцип суперпозиції будується на наступних властивостях розв’язків лінійних рівнянь:
-
Якщо
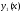 й
й
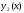 - два розв’язки однорідного лінійного
рівняння
- два розв’язки однорідного лінійного
рівняння
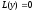 ,
то їхня лінійна комбінація
,
то їхня лінійна комбінація
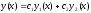 при будь-яких постійних
при будь-яких постійних
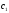 ,
,
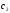 є рішенням диференціального рівняння.
є рішенням диференціального рівняння. -
Якщо
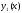 й
й
 - два розв’язки неоднорідного лінійного
рівняння
- два розв’язки неоднорідного лінійного
рівняння
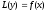 ,
то їхня різниця
,
то їхня різниця
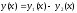 є рішенням однорідного рівняння
є рішенням однорідного рівняння
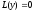 .
. -
Будь-яке розв’язок неоднорідного лінійного рівняння
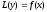 є сума частинного (фіксованого) розв’язку
неоднорідного рівняння й деякого
рішення однорідного рівняння.
є сума частинного (фіксованого) розв’язку
неоднорідного рівняння й деякого
рішення однорідного рівняння. -
Якщо
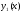 й
й
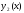 - розв’язки неоднорідних лінійних
рівнянь
- розв’язки неоднорідних лінійних
рівнянь
 і
і
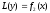 ,
то їхня сума
,
то їхня сума
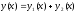 є розв’язок рівняння
є розв’язок рівняння
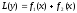 .
.
Наприклад,
функції
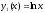 й
й
 - два розв’язок лінійного рівняння:
- два розв’язок лінійного рівняння:
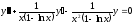 ,
,
а
функція
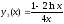 - розв’язок неоднорідного рівняння:
- розв’язок неоднорідного рівняння:
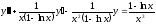 .
.
Підстановкою
в рівняння легко перевірити, що функція
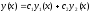 є розв’язок однорідного рівняння при
будь-яких
є розв’язок однорідного рівняння при
будь-яких
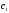 ,
,
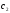 ,
а функція
,
а функція
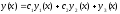 - розв’язок наведеного вище неоднорідного
рівняння.
- розв’язок наведеного вище неоднорідного
рівняння.
-
Загальний розв’язок лінійного однорідного рівняння з постійними коефіцієнтами
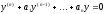 ,
,
где
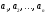 -
произвольные постоянные коэффициенты,
справедливы следующие утверждения.
-
произвольные постоянные коэффициенты,
справедливы следующие утверждения.
-
Существует
 линейно независимых решений
линейно независимых решений
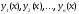 уравнения, а любые
уравнения, а любые
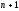 решений линейно зависимы.
решений линейно зависимы. -
При любых значениях констант
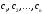 ,
функция
,
функция
 является решением уравнения.
является решением уравнения. -
Для любых начальных значений
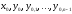 существуют такие значения
существуют такие значения
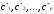 ,
что решение
,
что решение
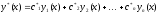 удовлетворяет условиям
удовлетворяет условиям
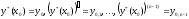
Выражение
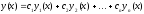 называется общим
решением
линейного однородного уравнения.
называется общим
решением
линейного однородного уравнения.
-
Линейные неоднородные уравнения с постоянными коэффициентами. Общее решение. Метод подбора.
В соответствии с принципом суперпозиции общее решение линейного неоднородного уравнения может быть записано как сумма общего решения однородного уравнения и любого частного решения неоднородного уравнения.
Метод подбора применяют для отыскания частных решений неоднородных уравнений с постоянными коэффициентами и правыми частями вида:
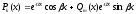
где
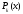 ,
,
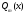 - многочлены соответственно степени
- многочлены соответственно степени
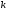 и
и
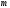 .
Правые части такого вида называют
обобщенными многочленами.
.
Правые части такого вида называют
обобщенными многочленами.
Метод подбора, или метод неопределенных коэффициентов, состоит в следующем.
Искомое решение уравнения записывается в виде:
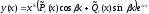 ,
,
где
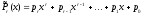 ,
,
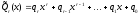 - многочлены степени
- многочлены степени
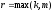 с неизвестными коэффициентами
с неизвестными коэффициентами
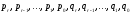 .
.
Сомножитель
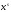 называют резонансным сомножителем.
Резонанс имеет место в случаях, когда
среди корней характеристического
уравнения есть корень
называют резонансным сомножителем.
Резонанс имеет место в случаях, когда
среди корней характеристического
уравнения есть корень
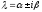 кратность
кратность
 ,
действительная часть которого совпадает
с коэффициентом в показателе степени
экспоненты, а мнимая – с коэффициентом
в аргументе тригонометрической функции
в правой части уравнения.
,
действительная часть которого совпадает
с коэффициентом в показателе степени
экспоненты, а мнимая – с коэффициентом
в аргументе тригонометрической функции
в правой части уравнения.
Подставив
выражение для решения с неопределенными
коэффициентами в левую часть уравнения,
получим обобщенный многочлен того же
вида, что и в правой части уравнения.
Два обобщенных многочлена равны тогда
и только тогда, когда равны коэффициенты
при сомножителях вида
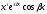 ,
,
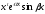 с одинаковыми степенями
с одинаковыми степенями
 .
Приравняв коэффициенты при таких
сомножителях, получим систему
.
Приравняв коэффициенты при таких
сомножителях, получим систему
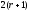 линейных алгебраических уравнений
относительно
линейных алгебраических уравнений
относительно
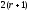 неизвестных. Решение системы – неизвестные
коэффициенты многочленов, входящие в
искомое выражение для частного решения
неоднородного дифференциального
уравнения.
неизвестных. Решение системы – неизвестные
коэффициенты многочленов, входящие в
искомое выражение для частного решения
неоднородного дифференциального
уравнения.
