Р ис. 3. Діаграма деформації розтягу стебла:

А – відповідає межі пропорційності, В – відповідає межі руйнування

б) визначити напруження, які відповідають межам пропорційності _ПЦ і міцності _МЦ.

Напруження _ПЦ (МПа), яке відповідає межі пропорційності

,

де F_ПЦ – навантаження, яке відповідає межі пропорційності, Н.

Напруження _МЦ (МПа), яке відповідає межі міцності

,

де F_РУЙН – навантаження, яке відповідає межі міцності, Н.

в) визначити модуль пружності Е_ПЦ і жорсткість стебла E_ПЦ S.

Модуль пружності (пропорційності) Е_ПЦ (МПа)

.

Жорсткість стебла рослини на розтяг (Н)

,

де _ПЦ – відносне подовження, яке відповідає межі пропорційності.

г) визначити потенціальну енергію пружної деформації А_ПР і роботу на руйнування стебла А_РУЙН.

Робота (енергія) пропорційна площі діаграми.

Потенціальна енергія пружної деформації А_ПР (Дж)

А_ПР = 0,5  F_ПЦ  l  10^{– 3}  k,

або

А_ПР = 0,5  _ПЦ  _ПЦ  10^{– 3}  k, k = S · l

де 0,5F_ПЦ l – площа трикутника діаграми, побудованої в координатах F – l;

0,5_ПЦ _ПЦ – площа трикутника діаграми, побудованої в координатах –;

k – коефіцієнт пропорційності для діаграми в координатах F – l дорівнює 1, для діаграми в координатах  –  дорівнює S· l. Розмірність S – мм², l – мм.

А_ПР = 0,5 89,2  0,88  10 ^{– 3}  1 = 39,25  10^{– 3} Дж = 0,0393 Дж.

або

А_ПР = 0,5  44,6  10⁶ Па  0,0088  2  10^{– 6} м²  100 м 10^{– 3} = 39,25  10^{– 3} Дж = 0,0393 Дж.

Роботу руйнування стебла (Дж) визначають за формулою

А_РУЙН = А_ПР + А^/,

де А^/ – робота, яку необхідно виконати за межами А_ПР. до руйнування, Дж.

Робота

А^/ = 0,5  (F_РУЙН + F_ПЦ)  (l_РУЙН – l_ПЦ)10^–3 · k,

А^/ = 0,5  (120 + 89,2)  (1,52 – 0,88)  10^–3 1 = 0,0669 Дж.

або

А^/ = 0,5  (_МЦ + _ПЦ)  (_РУЙН – _ПЦ) 10^–3  k; k = S  l.

А^/ = 0,5  (60 + 44,6)  10⁶  (0,0152 – 0,0088) 10^–3 · 2 · 10^{– 6}  100 = 0,0669 Дж.

А_РУЙН = 0,0393 Дж + 0,0669 Дж = 0,1062 Дж.

Відповідь: При розтязі стебла льону діаметром d = 1,6 мм і довжиною l = 100 мм модуль пружності (пропорційності) становить Е_ПЦ = 5068,18 МПа; жорсткість стебла рослини на розтяг - Потенціальна енергія пружної деформації А_ПР = 0,0393 Дж. Робота руйнування стебла А_РУЙН = 0,1062 Дж.

2. При деформуванні на поперечний стиск стебла озимої пшениці діаметром d одержано діаграму в координатах: зусилля F – абсолютне скорочення d з наступними даними:

F, H	0	1,67	3,34	5,02	6,69	8,93	10,47	11,45	11,96
d , мм	0	0,12	0,24	0,36	0,48	0,72	0,96	1,20	1,44

Довжина ділянки стебла, на яку діє сила F дорівнює в.

Необхідно:

а) побудувати діаграму деформації стиску стебла в координатах: величина умовного стискання q – відносне скорочення _С;

б) визначити модуль пружності Е_ПЦ;

в) визначити потенціальну енергію пружної деформації А_ПР і розплющування стебла А_РОЗПЛ..

Дано: d = 3,5 мм; в = 15 мм.

РОЗВЯЗОК:

а) побудувати діаграму деформації стиску стебла в координатах: величина умовного стискання q – відносне скорочення _С.

Опір стебел рослин стисканню.

Величина умовного стискання q (кПа)

,

де F – сила стискання, Н;

в – довжина ділянки стебла, на яку діє сила F, мм;

d – діаметр стебла, мм.

Проводимо розрахунки величин умовного стискання q

F, H

0

1,67

3,34

5,02

6,69

8,93

10,47

11,45

11,96

Відносна деформація

,

де d – абсолютне скорочення стебла, мм.

Проводимо розрахунки відносної величини деформації

d, мм

0

0,12

0,24

0,36

0,48

0,72

0,96

1,20

1,44

Після проведених розрахунків величини умовного стискання q та відносної величини деформації  заносимо в таблицю

qі, кПа	0	31,81	63,62	95,62	127,43	170,095	199,43	218,095	227,81
i	0	0,034	0,069	0,103	0,137	0,206	0,274	0,343	0,411

По отриманих даних малюємо діаграму деформації стиску стебла (рис. 4).

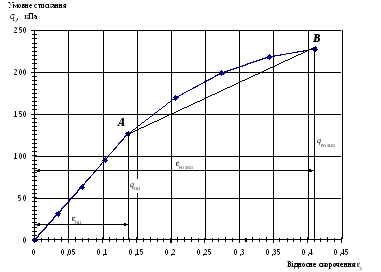
Рис. 4. Діаграма деформації стиску стебла:

А – відповідає межі пропорційності, В – відповідає розплющуванню.

б) визначити модуль пружності Е_ПЦ.

Модуль пропорційності (пружності), кПа

,

де q_ПЦ і _ПЦ – відповідно величина умовного стискання і відносної деформації, які відповідають межі пропорційності.

в) визначити потенціальну енергію пружної деформації А_ПР і розплющування стебла А_РОЗПЛ..

Потенціальна енергія (Дж) пружної деформації пропорційна площі трикутника, основою якого є _ПЦ, а висотою – q_ПЦ і дорівнює

A_ПР = 0,5  _ПЦ  q_ПЦ  10^–6  k,

де k = в d². Тут в і d підставляються в мм.

k = 15  3,5² = 183,75 мм³.

A_ПР = 0,5  0,137  127,43 10³ 183,75  10^–9 = 1604  10^–6 Дж = 0,0016 Дж.

Робота розплющування стебла А_РОЗПЛ (Дж) пропорційна з деяким наближенням сумі площ трикутника і трапеції, яка одержується проведенням хорди через точки q_ПЦ і q_РОЗПЛ..

А_РОЗПЛ= 0,5 [_ПЦ  q_ПЦ + (q_ПЦ + q_РОЗПЛ)  (_РОЗПЛ – _ПЦ)]  10^–6  k ².

А_РОЗПЛ = 0,5 10³  [0,137  127,43 + (127,43 + 227,81)  (0,411 – 0,137)]  10^–9  183,75 =

= 0,0105 Дж.

Відповідь: При деформуванні на поперечний стиск стебла озимої пшениці діаметром d = 3,5 мм модуль пропорційності (пружності) становить Е_ПЦ = 930,15 кПа. Потенціальна енергія пружної деформації A_Пр = 1,6010^–3 Дж. Робота розплющування стебла А_Роспл = 0,0105 Дж.

3. При згинанні консольнозакріпленого сухого стебла жита одержано залежності відгину у від прикладеної сили F:

F, H	0	0,05	0,10	0,15	0,20	0,25	0,29	0,31	0,33	0,35	0,37
у, мм	0	1,25	2,50	3,75	5,00	6,25	7,50	8,75	10,00	11,25	12,5

Необхідно:

а) побудувати залежність вигину у від сили F;

б) визначити потенціальну енергію пружної деформації А_ПР і роботу А_ЗЛ, необхідну для зламу стебел;

в) визначити жорсткість стебла Е_ПЦІ;

г) визначити осьовий момент інерції I;

д) визначити модуль пропорційності Е_ПЦ;

е) визначити кут відхилення стебла від горизонтального положення _ЗЛ.

Дано: d = 3,8 мм; l = 25 мм.

РОЗВЯЗОК:

а) побудувати залежність вигину у від сили F (рис. 5).

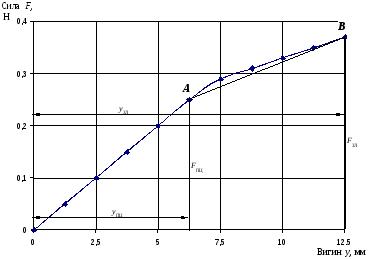
Рис. 5. Графік залежності вигину у від сили F:

А – відповідає межі пропорційності, В – відповідає зламу

б) визначити потенціальну енергію пружної деформації А_ПР і роботу А_ЗЛ, необхідну для зламу стебел.

Опір згинанню консольнозакріпленого стебла.

Потенціальна енергія пружної деформації А_ПР (Дж)

,

де F_ПЦ і у_ПЦ – відповідно навантаження (Н) і вигин (мм), які відповідають межі пропорційності.

Роботу, необхідну для зламу стебла, А_ЗЛ (Дж) обчислюють за формулою

,

де F_ЗЛ і у_ЗЛ – відповідно навантаження (Н) і вигин (мм), які відповідають межі міцності стебла.

в) визначити жорсткість стебла Е_ПЦІ.

Жорсткість стебла Е_ПЦІ (Н·м²)

,

де F – навантаження, яке відповідає вигину у_ПЦ, Н;

l – відстань від місця закріплення зразка до місця прикладання сили, мм;

I – осьовий момент інерції, м⁴.

г) визначити осьовий момент інерції I для трубчастого стебла.

Осьовий момент інерції I (м⁴)

для трубчастого стебла

,

де d_З – зовнішній діаметр стебла, м;

d_ВН – внутрішній діаметр стебла, м.

Товщина стінки стебел зернових культур складає 0,6 – 0,8 мм.

д) визначити модуль пропорційності Е_ПЦ.

е) визначити кут відхилення стебла від горизонтального положення _ЗЛ.

Кут зламу _ЗЛ (град.)

.

Відповідь: При згинанні консольнозакріпленого сухого стебла жита діаметром d = 3,8 мм і довжиною l = 25 мм потенціальна енергія пружної деформації становить А_ПР = 0,0078 Дж; робота, необхідна для зламу стебла буде А_ЗЛ = 0,027 Дж. Побудували залежність вигину від сили. Жорсткість стебла становить Е_ПЦІ = 1,310^-6 Н·м². Осьовий момент інерції становить I = 8,610^-12 м⁴. Кут відхилення стебла від горизонтального положення _ЗЛ становить майже 27 град.

4. При згинанні стебла соняшника діаметром d на двох опорах з відстанню між ними l одержано залежність прогину f зразка від прикладеного навантаження F:

F, H	0	7	14	21	28	35	42	48	56	51
f, мм	0	0,6	1,2	1,8	2,4	3,0	3,6	4,2	4,8	5,4

Необхідно:

а) побудувати залежність прогину f від навантаження F;

б) визначити модуль пружності Е­_ПЦ і жорсткість стебла ЕІ;

в) визначити потенціальну енергію пружної деформації А_ПР і роботу А_ЗЛ, необхідну для зламу стебла;

г) визначити кут зламу стебла _ЗЛ.

Дано: d = 22 мм; l = 100 мм.

РОЗВЯЗОК:

а) побудувати залежність прогину f від навантаження F (рис. 6).

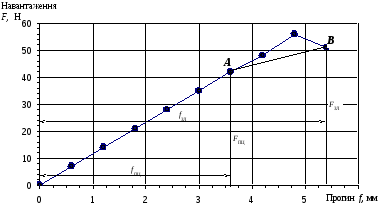
Рис. 6. Графік залежності прогину f від навантаження F:

А – відповідає межі пропорційності, В – відповідає зламу

б) визначити модуль пружності Е­_ПЦ і жорсткість стебла ЕІ.

Опір згинанню стебла, розташованого на двох опорах.

Жорсткість стебла Е_ПЦІ (Н·м²)

,

де F_ПЦ – навантаження, яке відповідає прогину f _ПЦ посередині між опорами, Н;

l – відстань між опорами, мм;

f_ПЦ – прогин, мм;

I – осьовий момент інерції, м⁴.

Осьовий момент інерції I (м⁴)

для трубчастого стебла

,

де d_З – зовнішній діаметр стебла (беремо згідно варіанту), мм;

d_ВН – внутрішній діаметр стебла (приймаємо товщину стінок даної культури 2 мм, тому діаметр внутрішній буде становити 18 мм), мм.

в) визначити потенціальну енергію пружної деформації А_ПР і роботу А_ЗЛ, необхідну для зламу стебла.

Потенціальна енергія пружної деформації А_ПР (Дж)

,

де F_ПЦ і f_ПЦ – відповідно навантаження (Н) і відгин (мм), які відповідають межі пропорційності.

Роботу, необхідну для зламу стебла, А_ЗЛ. (Дж) обчислюють за формулою

,

де F_ЗЛ і f_ЗЛ – відповідно навантаження (Н) і прогин (мм), які відповідають межі міцності стебла.

г) визначити кут зламу стебла _ЗЛ.

Кут зламу _ЗЛ (град.)

.

Відповідь: При згинанні консольно-закріпленого сухого стебла соняшника діаметром d = 3,8 мм і довжиною l = 100 мм потенціальна енергія пружної деформації А_ПР = 0,0756 Дж; робота, необхідна для зламу А_ЗЛ. = 0,1593 Дж.

5. При різанні без ковзання стебла кукурудзи діаметром d = 28 мм одержано діаграму в координатах: висота ординати h – переміщення сегмента l з наступними параметрами:

h, мм	0	7	14	21	28	36	20	0
l, мм	0	4	8	12	16	20	24	28

Масштаб пружини складає m.

Необхідно:

а) побудувати діаграму перерізання стебла залежністю h = f(l);

б) визначити величину максимального F_max і середнього F_C зусиль перерізання стебла;

в) визначити роботу різання стебла А_РІЗ;

г) визначити питому роботу різання а_РІЗ.

Дано: q_П = 9 Н/мм.

РОЗВЯЗОК:

а) побудувати діаграму перерізання стебла залежністю h = f(l) (рис. 7).

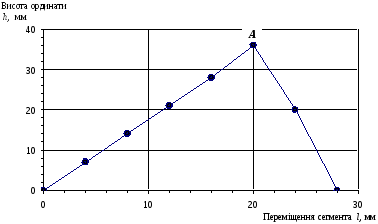
Рис. 7. Діаграма перерізання стебла залежністю h = f(l):

А – відповідає максимальній висоті ординат

б) визначити величину максимального F_max і середнього F_C зусиль перерізання стебла;

Величина максимального зусилля перерізання стебла F_max (Н)

,

де h_max – максимальна ордината діаграми, мм;

q_П – жорсткість (масштаб) пружини, Н/мм.

Величина середнього зусилля F_С (Н) перерізання стебла

,

де S_Д – площа діаграми, мм²;

l – переміщення сегмента, мм.