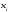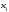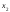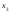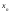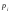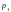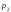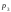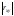Задания для контрольной работы №4
Задание № 1
Имеются статистические данные, что в суде, имеющих 6 комнат для заседаний, в xi комнатах одновременно проходят заседания с вероятностью рi (см. задания). Найти математическое ожидание и дисперсию случайной величины Х, имеющей смысл числа заседаний одновременно проходящих в случайный момент времени.
|
Число обслуживаемых клиентов (одинаково для всех вариантов). |
||||||||
|
xi
|
0
|
1
|
2
|
3
|
4
|
5
|
||
|
Вариант |
Вероятность pi (по вариантам) |
|||||||
|
1, 30
|
0,05
|
0,17
|
0,42
|
0,10
|
0,20
|
0,06
|
||
|
2, 29
|
0,39
|
0,10
|
0,18
|
0,15
|
0,11
|
0,07
|
||
|
3, 28
|
0,59
|
0,06
|
0,09
|
0,17
|
0,05
|
0,04
|
||
|
4, 27
|
0,13
|
0,15
|
0,45
|
0,12
|
0,08
|
0,07
|
||
|
5, 26
|
0,16
|
0,29
|
0,20
|
0,07
|
0,19
|
0,09
|
||
|
6, 25 |
0,16 |
0,21 |
0,47 |
0,02 |
0,10 |
0,04 |
||
|
7, 24
|
0,10
|
0,22
|
0,48
|
0,06
|
0,07
|
0,07
|
||
|
8, 23
|
0,34
|
0,08
|
0,34
|
0,01
|
0,17
|
0,06
|
||
|
9, 22
|
0,45
|
0,05
|
0,23
|
0,07
|
0,17
|
0,03
|
||
|
10, 21
|
0,26
|
0,07
|
0,44
|
0,07
|
0,07
|
0,09
|
||
|
11, 20
|
0,21
|
0,28
|
0,20
|
0,10
|
0,17
|
0,04
|
||
|
12, 19
|
0,45
|
0,08
|
0,06
|
0,19
|
0,18
|
0,04
|
||
|
13, 18
|
0,53
|
0,17
|
0,16
|
0,06
|
0,04
|
0,04
|
||
|
14, 17
|
0,38
|
0,13
|
0,06
|
0,18
|
0,19
|
0,06
|
||
|
15, 16
|
0,38
|
0,12
|
0,14
|
0,09
|
0,17
|
0,10
|
||
Задание № 2
Дана выборка количества приводов в милицию в течении года
для 20 детей из неблагополучных семей.
а) Составить статистический ряд по данным выборки.
б) Построить полигон, гистограмму кумуляту
Вариант ВЫБОРКА
1. 0 3 1 0 0 0 1 1 1 3 0 3 2 0 2 0 0 0 4 2
2. 3 4 1 6 1 4 1 1 2 0 2 5 3 1 1 1 2 6 2 3
3. 2 1 5 5 0 2 3 2 2 1 3 2 2 4 2 0 1 2 0 3
4. 5 2 1 1 2 3 0 2 3 2 1 1 0 0 4 2 0 1 1 2
5. 1 0 2 0 0 2 1 0 2 3 3 1 0 3 2 2 1 4 3 2
6. 0 2 2 1 3 0 2 1 3 3 2 4 2 0 0 2 3 0 2 0
7. 3 1 2 0 2 1 4 0 2 2 2 1 1 2 0 1 1 1 2 3
8. 1 3 1 0 2 5 3 3 1 0 3 0 2 2 1 3 2 3 5 0
9. 0 3 0 2 4 1 1 4 3 6 1 3 0 0 5 1 4 0 1 1
10. 0 0 0 3 0 3 2 1 2 1 1 1 0 1 3 0 1 1 3 0
11. 0 1 1 2 2 1 0 2 3 1 2 1 1 3 2 4 0 0 4 3
12. 1 1 2 2 1 2 0 1 0 0 1 2 1 4 1 1 0 1 1 0
13. 0 4 2 4 1 2 0 0 1 2 3 0 2 2 1 2 2 3 2 1
14. 0 1 2 0 0 0 0 0 2 3 3 1 0 0 2 1 1 3 2 1
15. 0 0 2 2 3 0 1 2 3 2 1 3 0 0 0 0 1 0 1 2
16. 3 0 2 3 0 2 2 1 0 3 2 2 0 2 0 1 1 3 0 2
17. 2 0 3 1 0 4 1 0 1 0 3 3 1 1 3 0 2 1 2 3
18. 3 1 0 2 1 0 2 1 1 5 0 2 4 1 2 1 2 0 4 3
19. 2 3 0 1 1 2 1 2 2 3 1 1 2 0 0 2 1 0 1 3
20. 2 0 2 0 1 2 3 0 3 1 4 3 1 2 2 1 1 3 2 1
21. 1 2 1 5 1 3 1 1 1 1 3 2 0 1 3 1 1 5 2 2
22. 1 4 1 1 0 0 3 2 1 1 1 2 1 1 3 0 0 1 0 2
23. 2 0 1 7 0 1 2 2 2 0 1 0 0 0 2 0 1 0 4 3
24. 2 2 0 0 1 2 2 4 0 1 3 1 6 0 1 0 2 1 1 0
25. 2 3 1 1 1 1 1 1 0 2 2 2 2 4 1 0 2 0 5 1
26. 0 0 1 1 1 2 2 3 4 1 0 1 2 1 0 2 2 0 3 4
27. 1 4 3 1 1 1 2 1 0 5 0 2 1 2 3 4 2 1 3 2
28. 2 3 2 1 3 0 3 1 1 2 3 2 2 1 2 2 3 1 3 0
29. 1 2 5 0 4 3 2 3 1 0 3 4 3 1 2 4 2 4 0 2
30. 3 1 3 4 1 1 1 2 2 0 0 2 2 0 4 2 1 5 2 1
Задание № 3.
Случайная величина X задана рядом распределения
|
X |
7 |
9 |
11 |
15 |
|
p |
0,14 |
0,2 |
0,49 |
0,17 |
Найти
функцию распределения F(x)
случайной величины X
и построить ее график. Найти для X
ее среднее значение (математическое
ожидание M(X)),
дисперсию D(X)
и моду
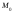
Решение:
а) Функцию распределения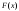
дискретной случайной величины X
найдем по формуле
,
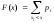которая может быть записана в виде
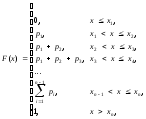
где закон распределения случайной величины X задан в виде таблицы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В нашем примере имеем:
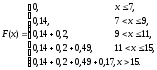
Таким образом, функция распределения примет вид
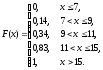
б) Математическое ожидание (среднее значение) дискретной случайной величины X найдем по формуле
.
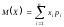Тогда математическое ожидание
.
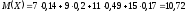в) Дисперсию дискретной случайной величины X найдем по формуле
,
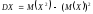где математическое ожидание квадрата дискретной случайной величины X
.
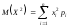Найдем
.
Тогда дисперсия
.
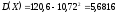г) Среднеквадратическое отклонение
.
д)
Моду
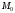найдем по максимальной вероятности в
ряде распределения:
.
Ответ: а) функция распределения
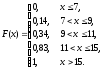
б)
математическое ожидание
;
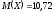в)
дисперсия
;
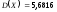г)
среднеквадратическое отклонение
;
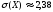д)
мода
.
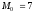Задание № 4.
На основании отчетных данных было проведено 10%-ное обследование строительных организаций по величине объема выполненных работ (млн. руб.). Полученные результаты представлены в таблице:
|
Объем работ, млн. руб. |
12-14 |
14-16 |
16-18 |
18-20 |
20-22 |
Итого |
|
Число организаций |
6 |
15 |
35 |
33 |
11 |
100 |
Используя
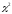-критерий
Пирсона, при уровне значимости
проверить гипотезу о том, что случайная
величина X
– величина объема выполненных работ –
распределена по нормальному закону.
Построить на одном чертеже гистограмму
эмпирического распределения и
соответствующую нормальную кривую.
Задание № 5.
Изучая зависимость между показателями X и Y, проведено обследование 9 объектов и получены следующие данные
|
X |
30 |
28 |
33 |
37 |
40 |
42 |
44 |
49 |
47 |
|
Y |
5 |
7 |
10 |
12 |
15 |
18 |
20 |
23 |
26 |
Полагая,
что между X
и Y
имеет место линейная корреляционная
связь, определите выборочное уравнение
регрессии
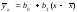и выборочный коэффициент линейной
регрессии
.
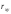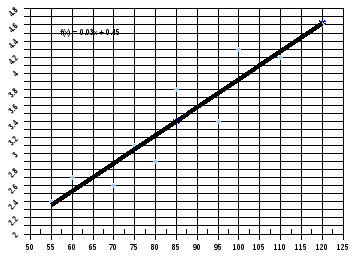
Постройте диаграмму рассеяния и линию
регрессии. Сделайте вывод о направлении
и тесноте связи между показателями X
и Y.
Решение.
Построим диаграмму рассеяния (рис.
1),
отметив в прямоугольной декартовой
системе координат точки с координатами
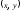- эмпирические данные. Из диаграммы
рассеяния видно, что между показателями
X
и Y
действительно наблюдается линейная
связь.
Для
определения коэффициентов выборочного
уравнения регрессии
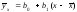можно воспользоваться, например,
следующими формулами
,
,
,
,
.
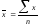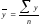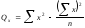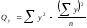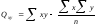Тогда
параметры
и
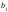уравнения линейной регрессии и выборочный
коэффициент линейной корреляции
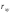определим по формулам
,
,
.
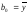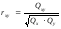Составим расчетную таблицу
|
|
x |
y |
x2 |
y2 |
xy |
|
1 |
30 |
5 |
900 |
25 |
150 |
|
2 |
28 |
7 |
784 |
49 |
196 |
|
3 |
33 |
10 |
1089 |
100 |
330 |
|
4 |
37 |
12 |
1369 |
144 |
444 |
|
5 |
40 |
15 |
1600 |
225 |
600 |
|
6 |
42 |
18 |
1764 |
324 |
756 |
|
7 |
44 |
20 |
1936 |
400 |
880 |
|
8 |
49 |
23 |
2401 |
529 |
1127 |
|
9 |
47 |
26 |
2209 |
676 |
1222 |
|
|
350 |
136 |
14052 |
2472 |
5705 |
Тогда
,
,
,
,
,
,
.
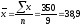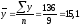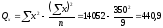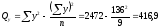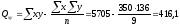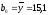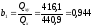Тогда выборочное уравнение линейной регрессии примет вид
,
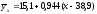или
.
Выборочный
коэффициент линейной корреляции
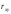
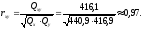
Таким
образом, расчеты подтвердили, что между
показателями X
и Y наблюдается
положительная линейная корреляционная
связь (связь прямая, так как
),
которая согласно таблице Чеддока можно
считать весьма высокой (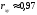
).
Для
построения линии регрессии (прямой)
найдем две точки. В качестве одной из
них можно выбрать
,
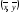то есть точку
.
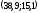Вторую точку найдем из уравнения
регрессии
.
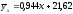При
:
,
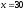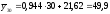то есть точка
.
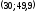Замечание
1. Выборочный
коэффициент линейной корреляции
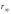меняется в пределах
.
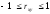Знак
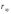характеризует направление, а абсолютная
величина
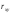- тесноту линейной корреляционной связи.
Если
,
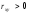то увеличение признака x
в среднем приводит к увеличению признака
y,
то есть связь между показателями x
и y
прямая (положительная) линейная
корреляционная связь. Если
,
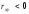то с увеличением признака x
в среднем признак y
уменьшается, то есть связь между
показателями x
и y
обратная (отрицательная) линейная
корреляционная связь.
Замечание 2. Для качественной оценки тесноты корреляционной связи между x и y можно воспользоваться таблицей Чеддока:
|
Диапазон
изменения
|
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,99 |
|
Характер тесноты связи |
слабая |
умеренная |
заметная |
высокая |
весьма высокая |
перерисовать