
Задания для контрольной работы №3
Задание № 1
Имеется 5 задержанных. Для проведения расследования необходимо устроить парные очные встречи каждого с каждым. Сколько таких встреч нужно организовать?
Задание № 2
В бригаде ОМОН 8 сотрудников. Для выполнения задания из них нужно отобрать группу из 5 человек. Сколько таких различных групп можно создать?
Задание 3. Бросают две игральные кости. Найти вероятность того, что на верхних гранях сумма числа очков не превосходит 7.
Решение. В данной задаче испытанием является бросание двух игральных костей. Результатом испытания является одно из сочетаний очков 1, 2, 3, 4, 5, 6 на верхних гранях двух костей.
Рассмотрим событие А - сумма числа очков на двух костях не превосходит 7, то есть указанная сумма меньше или равна 7.
Вероятность события А вычислим с помощью классического определения вероятности
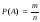 ,
,
где n – общее число равновозможных элементарных исходов испытания; m – число элементарных исходов благоприятствующих появлению события A.
Числа m и n можно определять, используя основные правила и понятия комбинаторики, а так же непосредственно выписав всевозможные результаты испытаний и выделив из них те, для которых сумма числа очков на двух костях не превосходит 7. Последним способом можно воспользоваться, воспользоваться, если общее число исходов и число исходов, благоприятствующих наступлению события A, не велико, как в нашем случае.
Составим таблицу всевозможных элементарных исходов данного испытания (в первом столбце по вертикали укажем число очков, которое может появиться на одной кости, в первой строке по горизонтали – число очков которое может появиться на второй кости, внутри таблицы запишем сумму числа очков на двух костях).
Таблица 1.
|
«+» |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Тогда
из табл. 1 несложно найти общее число
равновозможных элементарных исходов
испытания:
 (число клеток в табл. 1); и число элементарных
исходов благоприятствующих появлению
события A:
(число клеток в табл. 1); и число элементарных
исходов благоприятствующих появлению
события A:
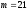 (число клеток в табл. 1, имеющих светлую
штриховку).
(число клеток в табл. 1, имеющих светлую
штриховку).
В результате получаем:
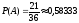 .
.
Таким образом, искомая вероятность равна 0,58333.
Ответ:
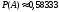
Задание 4. В ур-е содержится 7 черных и 4 белых шаров. Случайным образом вынимают 4 шаров. Найти вероятность того, что среди них имеется: а) 2 белых шаров;
б) меньше, чем 2, белых шаров;
в) хотя бы один белый шар.
Решение. В данной задаче испытанием является случайное вынимание четырех шаров. Элементарными событиями являются всевозможные сочетания по 4 из 11 шаров. Их число можно определить по формуле числа сочетаний из k по m:
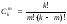 ,
,
где
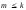 и
и
 (читается “«ка» факториал”) – есть
произведение первых k
натуральных чисел, то есть
(читается “«ка» факториал”) – есть
произведение первых k
натуральных чисел, то есть
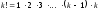 ,
причем по определению полагают, что
,
причем по определению полагают, что
 .
.
В
нашем случае
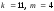 .
Тогда
.
Тогда
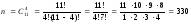
Решение: а) Рассмотрим событие А – среди четырех вынутых шаров 2 белых, то есть среди четырех вынутых шаров 2 белых и 2 черных.
Вероятность события А вычислим с помощью классического определения вероятности
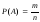 ,
,
где
n
– общее число равновозможных элементарных
исходов, испытания (в нашем случае
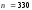 );
m
– число элементарных исходов
благоприятствующих появлению события
A.
);
m
– число элементарных исходов
благоприятствующих появлению события
A.
Для
нахождения m
воспользуемся правилом умножения: если
требуется выполнить одно за другим
какие-то
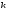 действий, которые можно выполнить
соответственно
действий, которые можно выполнить
соответственно
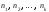 способами, то все
способами, то все
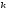 действий вместе могут быть выполнены
действий вместе могут быть выполнены
 способами.
способами.
В
нашем случае требуется выбрать из 4
белых шаров 2 шара и из 7 черных шаров
еще 2 шара. Из 4 шаров выбрать 2 шара можно
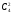 способами, из 7 шаров выбрать 2 шара можно
способами, из 7 шаров выбрать 2 шара можно
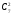 способами. Тогда число способов,
благоприятствующих событию
способами. Тогда число способов,
благоприятствующих событию
 определяется следующим выражением
определяется следующим выражением
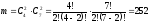 .
.
Тогда искомая вероятность:

Решение: б) Рассмотрим событие B – среди четырех вынутых шаров меньше чем 2 белых, то есть среди вынутых шаров или ни одного белого шара, а все четыре черные, или среди них один белый, а остальные три черные. Таким образом, событие B состоит из двух несовместных событий:
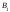 -
среди вынутых шаров только один белый
и 3 черных шара,
-
среди вынутых шаров только один белый
и 3 черных шара,
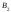 -
среди вынутых шаров нет ни одного белого,
все 4 шара черные, то есть
-
среди вынутых шаров нет ни одного белого,
все 4 шара черные, то есть
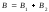 .
.
Так
как события
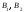 несовместны, то есть при осуществлении
одного из событий другое произойти не
может, то для нахождения вероятности
события
несовместны, то есть при осуществлении
одного из событий другое произойти не
может, то для нахождения вероятности
события
 можно воспользоваться или
теоремой
сложения для несовместных событий, или
классическим определением вероятности,
используя правило сложения.
можно воспользоваться или
теоремой
сложения для несовместных событий, или
классическим определением вероятности,
используя правило сложения.
Проиллюстрируем оба метода.
Первый
способ.
Используем теорему сложения для
несовместных событий, то есть если
события
 и
и
 несовместные, то вероятность суммы этих
событий
несовместные, то вероятность суммы этих
событий
 определяется следующей формулой
определяется следующей формулой
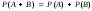 .
.
В
нашем случае имеем: события
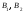 несовместны, тогда
несовместны, тогда
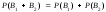 .
.
Вероятности
событий
 и
и
 определим, используя классическое
определение вероятностей.
определим, используя классическое
определение вероятностей.
Для
события
 имеем
имеем
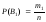 ,
,
где
 ,
,
 доделать(при
вычислении
доделать(при
вычислении
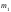 использовали правило умножения, так
как нам необходимо было определить
число способов, которыми можно выбрать
из 4 белых один шар и из 7 черных 3 шара,
и свойство числа сочетаний
использовали правило умножения, так
как нам необходимо было определить
число способов, которыми можно выбрать
из 4 белых один шар и из 7 черных 3 шара,
и свойство числа сочетаний
 ).
Тогда
).
Тогда
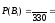 .
.
Для
события
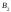 имеем
имеем
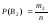 ,
,
где
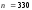 ,
,
 доделать(при
вычислении
доделать(при
вычислении
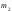 использовали
правило умножения, так как нам необходимо
было определить число способов, которыми
можно выбрать из 4 белых ноль шаров и из
7 черных 4 шара). Тогда
использовали
правило умножения, так как нам необходимо
было определить число способов, которыми
можно выбрать из 4 белых ноль шаров и из
7 черных 4 шара). Тогда
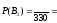 .
.
Таким образом, получим:
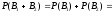 .
.
Второй
способ.
Для определения вероятности события
 воспользуемся классическим определением
вероятности
воспользуемся классическим определением
вероятности
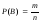 ,
,
где
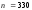 ;
а m
можно определить, используя правило
сложения.
;
а m
можно определить, используя правило
сложения.
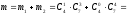
Тогда искомая вероятность
 .
.
Решение:
в)
Рассмотрим событие С
–
среди четырех вынутых шаров хотя бы
один белый. Этому событию удовлетворяют
следующие сочетания шаров: 1 белый и 3
черных (событие
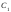 ),
2 белых и 2 черных (событие
),
2 белых и 2 черных (событие
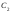 ),
3 белых и 1 черный (событие
),
3 белых и 1 черный (событие
 ),
4 белых и ни одного черного (событие
),
4 белых и ни одного черного (событие
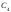 ).
Тогда
).
Тогда
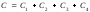 .
.
Здесь
событие C
определяется словами «хотя бы один» и
прямое решение приводит обычно к сложным
(громоздким) вычислениям. В таких задачах
удобнее вначале рассмотреть противоположное
событие
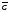 и найти его вероятность
и найти его вероятность
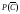 ,
а затем воспользоваться формулой
,
а затем воспользоваться формулой
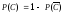 .
.
Рассмотрим
противоположное событие
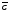 - среди четырех вынутых шаров нет ни
одного белого шара. Вероятность этого
события вычислим, используя классическое
определение вероятности
- среди четырех вынутых шаров нет ни
одного белого шара. Вероятность этого
события вычислим, используя классическое
определение вероятности
 ,
,
где
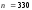 ,
,
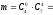 .
.
Таким образом, вероятность противоположного события
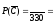 .
.
Тогда вероятность исходного события
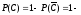 .
.
Ответ: ,
,
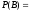 ,
,
 .
.
Задание 5. В каждом из 740 независимых испытаний событие А происходит с постоянной вероятностью 0,43. Найти вероятность того, что событие А происходит: а) точно 310 раз; б) меньше чем 310 и больше чем 266 раз; в) больше чем 310 раз.
Решение.
Так
как количество n
= 740
довольно велико, а вероятность p
=
0,43 не очень мала,
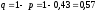 причем
причем
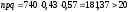 ,
,
то можно использовать формулы Муавра - Лапласа:
- локальная формула Муавра - Лапласа:
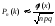 ,
,
где
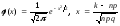 (таблица
значений функции
(таблица
значений функции
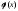 приведена в приложении 1 в настоящих
методических указаниях или в приложении
1 в книгах [1] или [5]; функция
приведена в приложении 1 в настоящих
методических указаниях или в приложении
1 в книгах [1] или [5]; функция
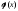 является четной, то есть
является четной, то есть
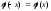 );
);
- интегральная формула Муавра – Лапласа:
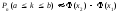 ,
,
где
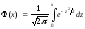 - функция Лапласа,
- функция Лапласа,
 ,
,
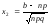 (таблица
функции Лапласа приведена в приложении
2 в настоящих методических указаниях
или в приложении 2 в книгах [1] или [5];
функция
(таблица
функции Лапласа приведена в приложении
2 в настоящих методических указаниях
или в приложении 2 в книгах [1] или [5];
функция
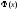 является нечетной, то есть
является нечетной, то есть
 ).
).
Решение:
a)
Дано:
 ,
,
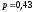 ,
,
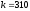 .
Найти вероятность
.
Найти вероятность
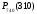 .
.
Воспользуемся локальной формулой Муавра – Лапласа
Находим
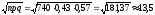 ;
;
Число получилось с минусом я без минуса делала
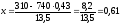 .
.
Значение
функции
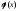 находим по таблице (приложение 1)
находим по таблице (приложение 1)
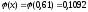 .
.
Тогда
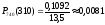 .
.
Решение:
б)
Дано:
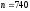 ,
,
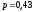 ,
,
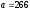 и
и
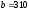 .
Найти вероятность
.
Найти вероятность
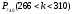 .
.
Воспользуемся
интегральной формулой Муавра – Лапласа
для нахождения вероятности

Находим
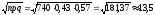 ;
;
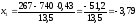 ;
;
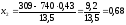 .
.
Значение
функции
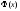 находим по таблице (приложение 2)
находим по таблице (приложение 2)
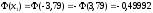 ;
;
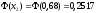 .
.
Тогда
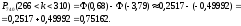
Решение:
в)
Дано:
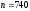 ,
,
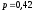 ,
,
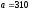 и
и
 .
Найти вероятность
.
Найти вероятность
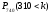 .
.
Воспользуемся
интегральной формулой Муавра – Лапласа
для нахождения
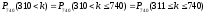 .
.
Находим
 ;
;
 ;
отрицательное
значение получилось
;
отрицательное
значение получилось
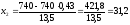 ;
;
Значение
функции
 находим по таблице (приложение 2)
находим по таблице (приложение 2)
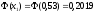 ;
;
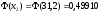 .
.
Тогда
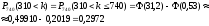
Ответ: 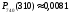 ;
;
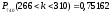 ;
;
 .
.
