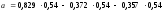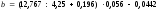Для вариантов 4,14,24,34
---------------------------------------------------------------------------------------------
Задание 1. Найдите пересечение, объединение, разность множества различных букв, входящих в слово «ГЕОМЕТРИЯ» и множества различных букв, входящих в слово «ХАЛАТНОСТЬ».
Решение:
Пусть
множество A
– множество различных букв, входящих
в слово «ГЕОМЕТРИЯ», т. е.
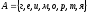 и пусть множество B
- – множество различных букв, входящих
в слово «ХАЛАТНОСТЬ», т. е.
и пусть множество B
- – множество различных букв, входящих
в слово «ХАЛАТНОСТЬ», т. е.
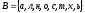 .
.
Тогда, по определению пересечения множеств A и B будем иметь
 .
.
По определению объединения множеств A и B будем иметь
 .
.
По
определению разности множеств A
и B,
получим
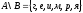
Ответ:
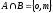 ;
;
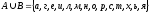 ;
;
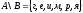 .
.
----------------------------------------------------------------------------------------------
Задание
2. 1).
Укажите характеристическое свойство
элементов множества
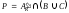 ,
если
,
если
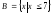 ,
,
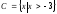 и
и
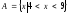 .
2). Изобразить на числовых прямых все
множества. 3). Выясните, истинны ли
высказывания
.
2). Изобразить на числовых прямых все
множества. 3). Выясните, истинны ли
высказывания
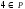 ,
,
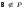 ,
, .
.
Решение:
1). Изобразим на числовых прямых заданные
множества (рис.1). Учитывая
соглашение о порядке выполнения операций,
сначала находим
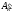 ,
затем
,
затем
------------------------------------------------------------------------------------------
Задание
3. Докажите,
что для любых множеств A,
B,
C
справедливо равенство:
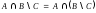 ,
и проиллюстрируйте его с помощью кругов
Эйлера.
,
и проиллюстрируйте его с помощью кругов
Эйлера.
Решение: Для доказательства равенства множеств
Задание 4. Из 300 человек плаванием занимается 200 человек, а прыжками в воду – 120 человек, Найти наибольшее и наименьшее число человек, занимающихся обоими видами спорта
Задание 5. Составить таблицу истинности для следующего высказывания. Выяснить является ли данное высказывание тавтологией?
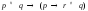
Задания для контрольной работы №2
Задание № 1
Даны множества A и В. Найти AB, AB, A\ B, B \ A, AB.
множество А - 0 1 7 8 9 11 12 14
множество В - 0 2 3 5 7 11 12 15
Задание № 2
В юридической фирме 25 юристов являются специалистами по гражданскому праву, 27 – по уголовному, 22- по административному. Кроме того 9 сотрудников являются специалистами по гражданскому и уголовному, 8 – по уголовному и административному, 7 – по гражданскому и административному, а 3 сотрудника являются специалистами во всех трех правах. Сколько сотрудников работает в фирме?
Вар-т N1 N2 N3 N4 N5 N6 N7
4. 25 27 22 9 8 7 3
Задание № 3
Дана логическая функция ((xy) ( y z)). Составить таблицу истинности.
Задание № 4
Доказать методом математической индукции, что для любого натурального числа n истинно равенство
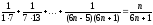
Решение :
а).
При n
= 1 данное утверждение истинно: в левой
части равенства имеем:
 ;
в
правой части равенства:
;
в
правой части равенства:
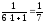 .
.
б).
Докажем теперь, что если утверждение
истинно для n
= k
, т.е.
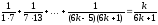 ,
то
оно истинно и для n
= k
+ 1, т.е.
,
то
оно истинно и для n
= k
+ 1, т.е.
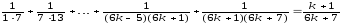
В
выражении: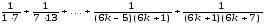
сумма
первых k
слагаемых по условию равна
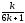 ,
что
дает возможность привести данное
выражение к виду
,
что
дает возможность привести данное
выражение к виду
 .
.
Дальнейшее преобразования полученного выражения приводят к следующему:
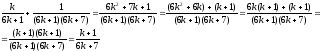
Таким образом,
 что
и требовалось доказать на этом этапе.
что
и требовалось доказать на этом этапе.
Таким образом, мы доказали, что из того, что формула верна при n = k, следует, что она верна и при n = k +1.
На основании метода математической индукции заключаем, что данное равенство истинно для любого натурального n.
Задание № 5
Не используя калькулятор, выразите в процентах частное чисел a и b, если