Кривые упрочнения

Истинное напряжение является пределом текучести упрочненного наклепом материала. Иногда его называют напряжением текучести. Зависимость между сопротивлением деформации, т. е. напряжением текучести, и степенью деформации изображают кривыми упрочнения. При построении кривых упрочнения по оси ординат обычно откладывают напряжение текучести , а по оси абсцисс — относительную деформацию.

В зависимости от вида характеристики относительной деформации при растяжении обычно различают три вида кривых упрочнения:

первый вид устанавливает зависимость от относительного удлинения;

второй вид — зависимость от сужения площади ;

третий вид — зависимость от «истинного» сужения площади .

В пределах равномерного удлинения образца, т. е. до момента образования шейки, между тремя видами деформации () легко установить следующие соотношения.

По условию постоянства объема , где F_ol_o — площадь поперечного сечения и длина образца в исходном состоянии; F — площадь поперечного сечения образца в момент, когда абсолютное удлинение равно . Отсюда

; (1.1)

; (1.1a)

; (1.2)

(1.3)

(1.4)

Ниже рассмотрены некоторые важные особенности кривых упрочнения. Полная нагрузка на образец, в каждый момент времени. P=F. Дифференцируя это выражение, получаем dP = dF+dF.

Полная нагрузка достигает максимального значения в момент начала образования шейки, когда условное напряжение достигает предела прочности . Следовательно,

(1.5)

Используя (1.5), рассмотрим свойства кривой упрочнения первого вида. Так как до момента образования шейки справедливы соотношения (1.1) и (1.1а),

(1.6)

Следовательно,

(1.7)

и (1.8)

Но равно тангенсу угла наклона касательной к кривой упрочнения первого вида в точке начала образования шейки (рис. 2), т. е.

(1.9)

Отсюда следует, что касательная к кривой упрочне­ния первого вида в точке начала образования шейки от­секает на отрицательной оси абсцисс отрезок, численно равный единице удлинения. Отрезок, отсекаемый каса­тельной на оси ординат,

(1.10)

Полная нагрузка в момент образования шейки достигает максимального значения .

Следовательно,

… (1.11)

Подставив значение в (1.10), получим

… (1.12)

Касательная к кривой упрочнения первого вида в точке начала образования шейки отсекает на оси орди­нат отрезок, численно равный пределу прочности. Из подобия треугольников АОС и ADB получаем, что при .

Касательная к кривой упрочнения первого вида в точке начала образования' шейки отсекает на ординате, равной единице относительного удлинения, отрезок, равный удвоенному пределу прочности.

Рассмотрим свойства кривой упрочнения второго вида, которая имеет преимущество перед кривой перво­го вида, так как относительное удлинение после обра­зования шейки зависит от расчетной длины образца. Сужение площади поперечного сечения не зависит от формы образца.

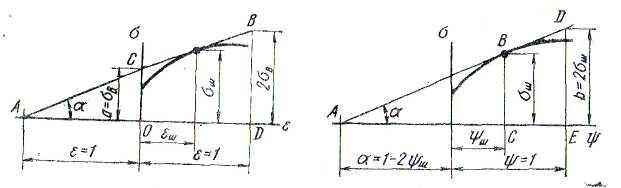
Рис.2. Кривая упрочнения Рис.3. Кривая упрочнения

первого вида второго вида

Кроме того, оно изменяется от нуля до единицы, тогда как относительное удлинение может, быть неограниченной величиной.

Из выражения (1.2) F=F₀(1—) следует dF= - F₀d.

Подставляя значения F и dF, отвечающие моменту образования шейки, в выражение (1.9), получаем

, (1.13)

где — угол наклона касательной к кривой упрочнения в точке начала образования шейки (рис. 3).

Из треугольника ABC определим расстояние точки пересечения касательной с осью абсцисс до начала ко­ординат :

(1.14)

отсюда .

Касательная к кривой упрочнения второго вида в точке начала образования шейки отсекает на отрицательной оси абсцисс отрезок, равный .

Из треугольника ADE определяем конечную ордина­ту b, когда ,

отсюда

Разность 2σ_ш - σ₀ называют модулем упрочнения.

Свойства кривой упрочнения третьего вида. Из выражения (1.4) следует, что .

Полная нагрузка при растяжении

. (1.15)

Дифференцируя это выражение, получаем

В момент образования шейки на образце нагрузка достигает максимального значения, поэтому

Отсюда

Из рис. 4 следует, что касательная к кривой упрочнения третьего вида в точке начала образования шейки отсекает на отрицательной оси абсцисс отрезок, равный .

И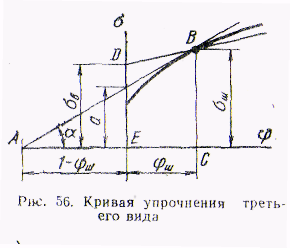з подобия треугольни­ков ABC и ADE находим Рис.4 Кривая упрочнения третьего вида

Следовательно, касательная к кривой упрочнения третьего вида в точке начала образования шейки отсекает на оси ординат отрезок, численно равный .

Задача

При испытании на растяжение определены: предел прочности =45 кгс/мм², сужение площади в момент образования шейки = 0,1. Определить истинное сопротивление деформации при относительном удлинении = 0,4.

Решение

Воспользуемся кривой упрочнения второго вида. Определим сужение площади , отвечающее удлинению 0,4:

Истинное сопротивление в момент образования шейки:

кгс/мм².

Определяем приближенное значение истинного сопротивления деформации при = 0,286 по касательной к кривой:

кгс/мм

Определяем по приближенному уравнению кривой второго вида:

кгс/мм.