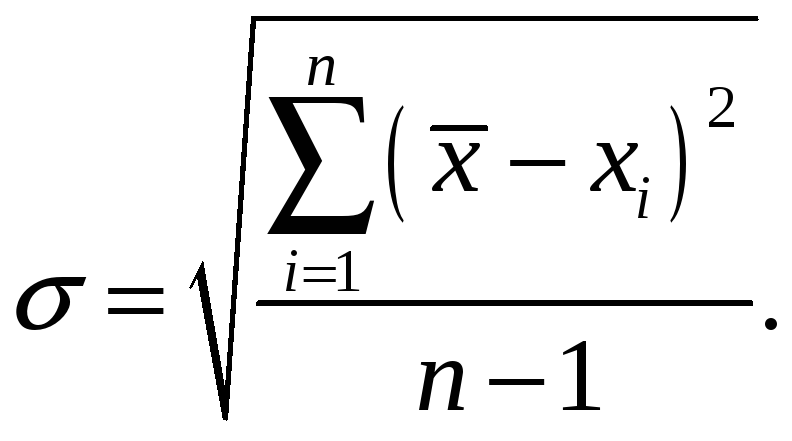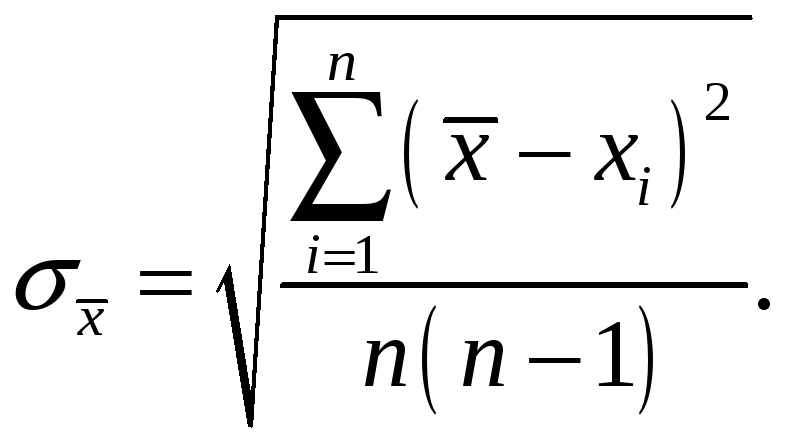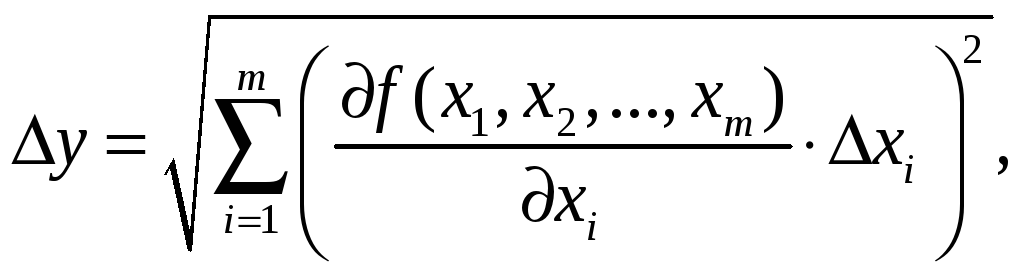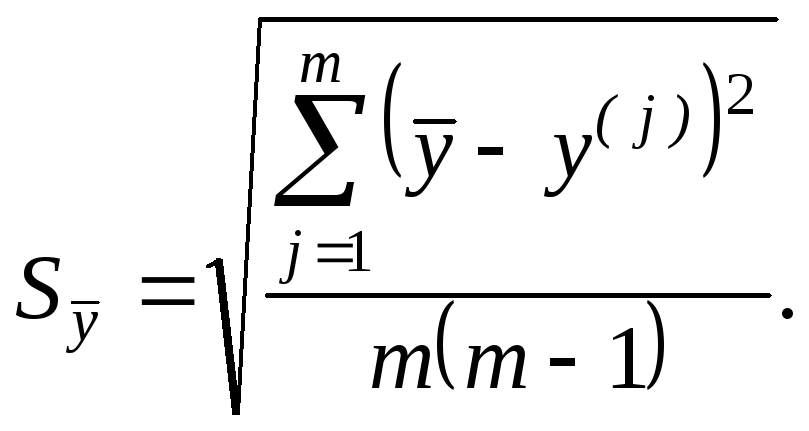- •Оценка погрешностей измерений
- •4. Термодинамика
- •Теоретическая часть
- •Методика и порядок проведения работы
- •Результаты работы
- •Вопросы для самоконтроля
- •Обработка результатов
- •Вопросы для самоконтроля
- •Теоретические сведения
- •Результаты опыта
- •Вопросы для самоконтроля
- •5. Растворы
- •Теоретические сведения
Министерство образования и науки РФ
ФГАОУ ВПО
«Уральский федеральный университет имени первого Президента России Б.Н. Ельцина»
ТЕРМОДИНАМИКА. РАСТВОРЫ
Методические указания к лабораторным работам
по курсу «Физическая химия»
для студентов всех форм обучения металлургических специальностей
Екатеринбург
2010
УДК 541.1
Составители: А.И. Михайлов, Н.Ю. Добрынина, Л.Н. Шибанова
Научный редактор: А.М. Панфилов
ТЕРМОДИНАМИКА. РАСТВОРЫ: Методические указания к лабораторным работам по курсу «Физическая химия»/ А.И. Михайлов, Н.Ю. Добрынина, Л.Н. Шибанова. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2010. 51 с.
Методические указания предназначены для организации самостоятельной работы студентов всех видов обучения металлургических специальностей при выполнении лабораторных работ по курсу «Физическая химия».
В работе изложены теория и методика выполнения шести лабораторных работ, предусмотренных учебными программами курса «Физическая химия» (разделы «Термодинамика», «Термодинамика растворов»): изучение равновесия реакций газификации углерода и диссоциации карбонатов на примере CaCO3, определение теплот растворения солей в воде и коэффициента распределения вещества между двумя несмешивающимися жидкостями, определение парциально-молярных объемов компонентов в бинарных растворах, изучение концентрационной зависимости температуры замерзания раствора. Приведены необходимые справочные данные, изложена методика оценки погрешности измерений.
Библиогр.: 5 назв. Рис. 13. Табл. 8. Прил. 3.
|
|
Подготовлено кафедрой «Теория металлургических процессов»
|
© ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина», 2010.
СОДЕРЖАНИЕ
|
ВВЕДЕНИЕ |
4 |
|
|
1. ОСНОВНЫЕ ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К СТУДЕНТАМ В ЛАБОРАТОРИИ |
4 |
|
|
2. ПОСТРОЕНИЕ ГРАФИКОВ |
6 |
|
|
3. ОЦЕНКА ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ |
7 |
|
|
4. ТЕРМОДИНАМИКА |
11 |
|
|
Работа № 1. |
ИЗУЧЕНИЕ РАВНОВЕСИЯ РЕАКЦИИ ГАЗИФИКАЦИИ УГЛЕРОДА ЕГО ДИОКСИДОМ |
11 |
|
Работа № 2. |
ИЗУЧЕНИЕ УПРУГОСТИ ДИССОЦИАЦИИ CaCO3 |
19 |
|
Работа № 3 |
ОПРЕДЕЛЕНИЕ ТЕПЛОТЫ РАСТВОРЕНИЯ СОЛИ В ВОДЕ |
25 |
|
5. РАСТВОРЫ |
31 |
|
|
Работа № 4.
|
ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА РАСПРЕДЕЛЕНИЯ ВЕЩЕСТВА В ДВУХ НЕСМЕШИВАЮЩИХСЯ ЖИДКОСТЯХ |
31 |
|
Работа № 5. |
ОПРЕДЕЛЕНИЕ ПАРЦИАЛЬНО-МОЛЯРНЫХ ОБЪЕМОВ КОМПОНЕНТОВ БИНАРНОГО РАСТВОРА |
38 |
|
Работа № 6. |
ОПРЕДЕЛЕНИЕ КРИОСКОПИЧЕСКОЙ ПОСТОЯННОЙ ВОДЫ |
45 |
|
ПРИЛОЖЕНИЕ 1 |
Термодинамические свойства некоторых веществ |
53 |
|
ПРИЛОЖЕНИЕ 2 |
Расчет
величины
|
53 |
|
ПРИЛОЖЕНИЕ 3 |
Интегральные теплоты растворения некоторых солей в воде при 25ºС |
53 |
|
Библиографический список |
54 |
|
ВВЕДЕНИЕ
Выполнение лабораторных работ по физической химии дает возможность более глубокого осмысления студентами соответствующих разделов теоретического курса, знакомит с некоторыми методами физико-химических исследований, закрепляет необходимые навыки самостоятельной обработки и анализа результатов наблюдений.
-
ОСНОВНЫЕ ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К СТУДЕНТАМ В ЛАБОРАТОРИИ
-
Техника безопасности
-
К выполнению лабораторных работ допускаются только лица,
прошедшие вводный инструктаж по технике безопасности и имеющие соответствующую подпись в листке по учёту инструктажа.
Работа с нагревательными и измерительными электрическими приборами, с химической посудой и реактивами проводится согласно инструкции по технике безопасности в лаборатории.
После выполнения работы студент приводит в порядок рабочее место и сдает его лаборанту.
-
Особенности подготовки к лабораторным занятиям
Основными источниками для подготовки к занятиям являются «Методические указания к лабораторным работам», учебники и учебные пособия, рекомендованные лектором, конспекты лекций.
Готовясь к лабораторной работе, студент в течение недели, предшествующей занятию,
должен прочитать и понять материал, изложенный в методических указаниях к лабораторным работам, и подготовить теоретическую часть отчета в соответствии с требованиями, указанными ниже. При возникновении затруднений необходимо использовать рекомендованную литературу, а также конспекты лекций, консультации лектора и преподавателей, ведущих лабораторные занятия.
Готовность студента к выполнению работы контролируется преподавателем путем опроса каждого из студентов. Недостаточно подготовленный студент обязан изучить материал, относящийся к данной работе, в течение занятия, а экспериментальную часть работы выполнить на дополнительном занятии, дата и время проведения которого указываются преподавателем.
-
Требования к отчету
Отчет о лабораторной работе пишется на развернутых листах из тетради и состоит из следующих разделов:
-
Лицевая сторона отчета (образец приведен на рис. 1).

-
Теоретическая часть работы – конспект соответствующего раздела методических указаний к лабораторным работам. В конспекте необходимо изложить цель работы, краткое
описание изучаемых физико-химических свойств систем или процессов, расчетные формулы с пояснением физического смысла входящих в них величин.
-
Эскиз схемы установки с обозначением приборов и основных узлов, используемых
в эксперименте.
Разделы 1.3.1 – 1.3.3 должны быть выполнены в процессе подготовки к работе.
-
Перечень средств измерений с указанием измеряемых величин.
-
Таблица первичных опытных данных и величин, подлежащих определению.
Рекомендуется результаты измерений фиксировать на черновике и переносить в отчет после проверки их преподавателем.
-
Произведенные вычисления, расчет погрешностей определения величин, если он
предусмотрен в методических указаниях.
-
Графики изучаемых зависимостей, построенные в соответствии с требованиями,
изложенными ниже в разделе 2.
-
Выводы по работе, в которых необходимо отразить:
– на основании каких опытных данных делается то или иное заключение;
– согласуются ли сделанные заключения с изученными ранее физико-химическими закономерностями;
– возможные причины отклонения от ожидаемых результатов (если таковые имеются).
Выводы следует излагать литературным языком, допуская лишь общепринятые сокращения. Полностью оформленный отчет о работе сдается на проверку преподавателю перед началом следующей работы или заранее в часы консультации.
-
ПОСТРОЕНИЕ ГРАФИКОВ
Графическое изображение опытных и расчетных данных облегчает сравнение величин, позволяет легко обнаружить характер изменения их (наличие максимумов, минимумов, точек перегиба и т.п.). В таблицах все эти особенности проявляются менее отчетливо.
При построении графиков необходимо соблюдать следующие основные правила:
-
Значение независимой переменной откладывают по оси абсцисс,
функции – по оси ординат.
-
Масштабы нужно выбирать так, чтобы координаты любой точки графика могли быть
определены легко и быстро. Если расстояние между главными соседними линиями разделено на десять равных частей, то наиболее удобно выбирать такой масштаб, в котором это расстояние принято за одну, две, четыре или пять единиц. Цифровые обозначения этих величин необходимо проставлять равномерно вдоль всей оси. На каждой координатной оси необходимо проставить название представляемой ею величины и единицы, в которых она измеряется.
При выборе шкалы по осям координат нет необходимости откладывать величины с нулевого значения, если это не вызвано специальными соображениями (экстраполяция и т.п.). В соответствии с этим правилом шкала для каждой переменной величины может начинаться с наименьшего округленного значения из совокупности данных и заканчиваться округленным в сторону большего значения.
-
Масштаб желательно выбирать так, чтобы кривая проходила через всё поле графика,
насколько это возможно.
-
Кривая должна быть плавной, проходить насколько возможно близко ко всем
нанесенным точкам. Примерно одна половина всех точек должна лежать по одну сторону кривой, а вторая – по другую. Кривая не должна содержать необъяснимых разрывов, самопересечений или других подобных особенностей.
Рекомендуется на графике четко выделять опытные точки, а кривую, проведенную по
ним, представлять сравнительно тонкой линией. На линиях, полученных в результате теоретических расчетов, точки не проставляются.
-
Оценка погрешностей измерений
1.3 Общие положения
При выполнении измерений результат
всегда получается с некоторой погрешностью.
Погрешностью измерений называют величину
![]() ,
определяемую из неравенства
,
определяемую из неравенства
|
|
(1) |
где
![]() –
истинное значение измеряемой величины,
–
истинное значение измеряемой величины,
![]() –
измеренное значение величины.
–
измеренное значение величины.
Поскольку
точное значение
![]() не известно, точно узнать
не известно, точно узнать
![]() нельзя. Поэтому указывают интервал
нельзя. Поэтому указывают интервал
![]() ,
внутри которого с определенной
вероятностью, называемой доверительной
вероятностью, расположено значение
,
внутри которого с определенной
вероятностью, называемой доверительной
вероятностью, расположено значение
![]() .
.
За лучшую оценку истинного значения результата измерений, принимают
среднее
арифметическое (![]() )
из всех величин
)
из всех величин
![]() ,
полученных в процессе отдельных
измерений, выполненных в одинаковых
условиях:
,
полученных в процессе отдельных
измерений, выполненных в одинаковых
условиях:
|
|
(2) |
где n – число отдельных измерений.
Качество
результатов измерений бывает удобно
характеризовать не абсолютной погрешностью
![]() ,
а ее отношением к найденному значению
измеряемой величины
,
а ее отношением к найденному значению
измеряемой величины
![]() ,
которое называют относительной
погрешностью a
и выражают в процентах:
,
которое называют относительной
погрешностью a
и выражают в процентах:
|
|
(3) |
Погрешности измерений принято подразделять на систематические, случайные и грубые.
Грубые погрешности (промахи) появляются из-за недостатка внимания экспериментатора. Грубая погрешность обычно существенно превышает случайную.
3.2 Систематические погрешности
Систематические погрешности δ вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Систематическую погрешность можно оценить, сравнив полученные результаты измерений с расчетным значением измеряемой величины, найденным на основании более точных экспериментальных данных, приведенных в справочнике.
3.3 Случайные погрешности
Случайные
погрешности обязаны своим происхождением
ряду причин, действие которых неодинаково
в каждом опыте и не может быть учтено.
Чаще всего случайные погрешности
подчиняются нормальному закону
распределения и могут быть оценены с
помощью выборочной средней квадратической
погрешности отдельного измерения (![]() ):
):
|
|
(4) |
При
большом числе измерений (![]() )
можно утверждать, что точное значение
измеряемой величины
)
можно утверждать, что точное значение
измеряемой величины
![]() лежит в интервале
лежит в интервале
![]() с доверительной вероятностью 0.68 или в
интервале
с доверительной вероятностью 0.68 или в
интервале
![]() с вероятностью 0.95.
с вероятностью 0.95.
Если
для нахождения определенного значения
физической величины проводят несколько
(n)
параллельных измерений, а затем по
формуле (2) рассчитывают их среднее
значение
![]() ,
то средняя квадратическая погрешность
среднего арифметического
,
то средняя квадратическая погрешность
среднего арифметического
![]() будет меньше погрешности отдельного
измерения
будет меньше погрешности отдельного
измерения
![]() в
в
![]() раз:
раз:
|
|
(5) |
В
предлагаемых лабораторных работах
случайную погрешность измерений следует
оценивать по формуле (4) на основании
нескольких измерений (![]() ),
выполненных в одинаковых условиях.
),
выполненных в одинаковых условиях.
3.4 Учет систематической и случайной погрешностей
Часто
бывает, что систематическая и случайная
погрешности близки друг другу и обе
определяют точность результата. Тогда
можно найти суммарную погрешность
![]() ,
полагая, что систематической погрешности
,
полагая, что систематической погрешности
![]() соответствует не бόльшая доверительная
вероятность, чем утроенной
среднеквадратической погрешности
соответствует не бόльшая доверительная
вероятность, чем утроенной
среднеквадратической погрешности
![]() :
:
|
|
(6) |
3.5 Погрешности косвенных измерений
Измерения
подразделяются на прямые
и косвенные.
При прямом измерении искомую величину
определяют непосредственно с помощью
измерительного устройства, например
находят высоту поднятия жидкости в
манометре с помощью измерительной
линейки. Результат косвенных измерений
вычисляют по данным прямых измерений
с помощью формул. Например, в работе №
1 средний тепловой эффект реакции
![]() находят по опытным данным с помощью
формулы (см. приложение 2)
находят по опытным данным с помощью
формулы (см. приложение 2)
![]()
Погрешности прямых измерений могут
быть найдены по соотношениям (3.4), (3.5) и
(3.6). Если при косвенных измерениях
интересующая нас величина
![]() является известной функцией других
величин
является известной функцией других
величин
![]() ,
которые измеряются непосредственно
,
которые измеряются непосредственно
|
|
(7) |
то
ее абсолютную погрешность
![]() можно найти как
можно найти как
|
|
(8) |
где
![]() – абсолютная погрешность величины
– абсолютная погрешность величины
![]() .
.
Лучшим
приближением к истинному значению
![]() ,
как и в случае прямых измерений, считают
среднее арифметическое значение
,
как и в случае прямых измерений, считают
среднее арифметическое значение
![]() .
.
Среднеарифметическое
значение измеряемой величины
![]() и погрешность результата можно вычислить
двумя способами:
и погрешность результата можно вычислить
двумя способами:
-
Вычислить
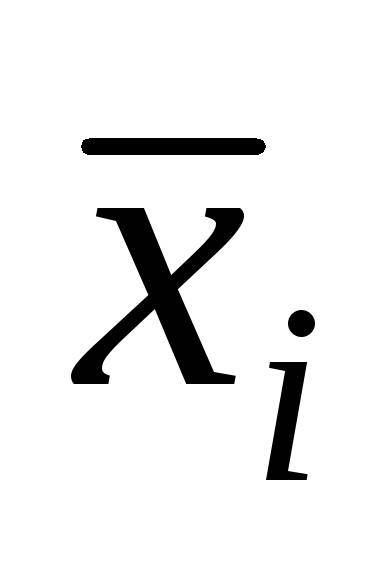 и, подставив эти значения в уравнение
(3.7), найти
и, подставив эти значения в уравнение
(3.7), найти
 .
Затем, определив погрешности
.
Затем, определив погрешности
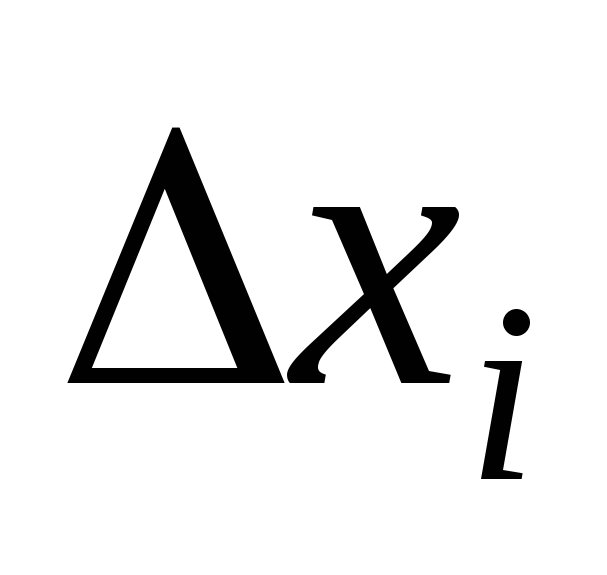 , по уравнению (3.8) найти
, по уравнению (3.8) найти
 .
. -
Для каждой группы результатов совместных измерений (
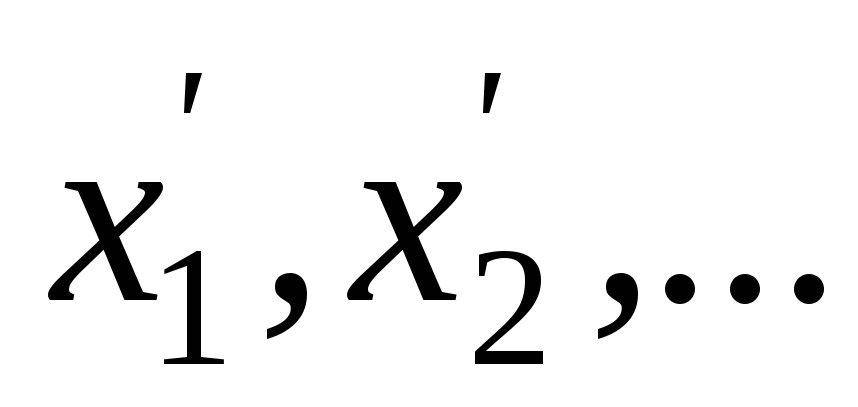 );
(
);
(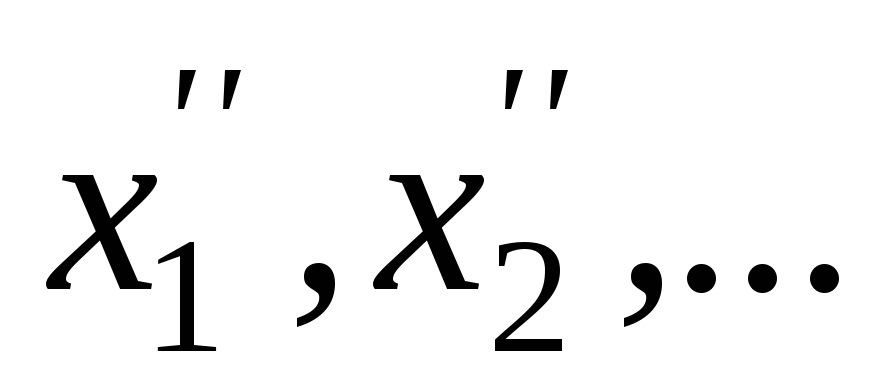 ),
…; (
),
…; (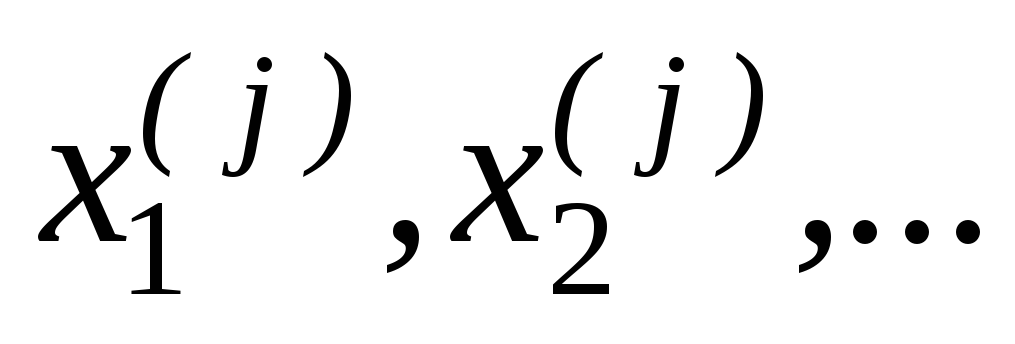 );
…; (
);
…; (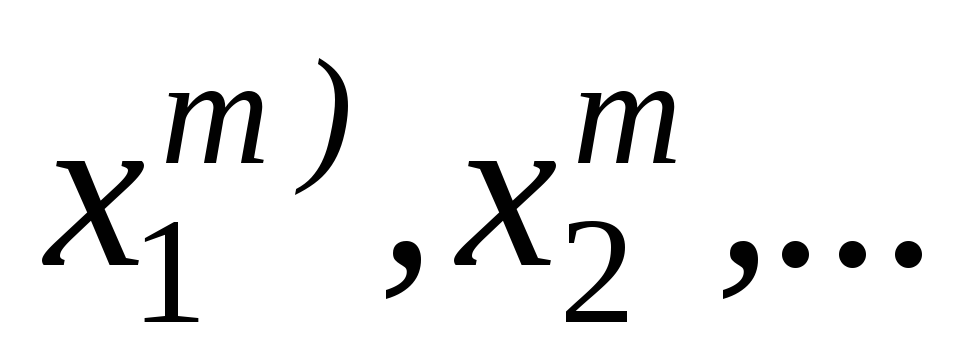 )
найти
)
найти
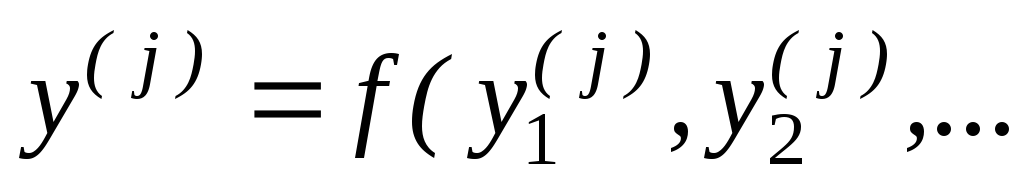 ,
затем рассчитать среднеарифметическое
значение
,
затем рассчитать среднеарифметическое
значение
 :
:
|
|
(9) |
а погрешность определения величины вычислить обычным путем:
|
|
(10) |
Систематическую
погрешность косвенных измерений, как
и прямых, можно оценить путем сравнения
![]() с результатами расчетов, выполненных
с использованием справочных данных.
с результатами расчетов, выполненных
с использованием справочных данных.
3.6 Требуемая точность вычислений. Целесообразное число значащих цифр в представлении результатов измерений
Во всех случаях нужно придерживаться следующего правила. Погрешность, получающаяся в результате вычислений, должна быть на порядок (т.е. в 10 раз) меньше суммарной погрешности измерений. При этом можно быть уверенным, что в процессе арифметических операций мы ощутимым образом не исказили результата.
Как окончательный результат вычислений записывают числа только с верными цифрами и одной сомнительной (так называется цифра того разряда, в котором содержится первая значащая цифра ошибки). Неверные цифры (правее сомнительной) отбрасывают с соблюдением правил округления. Следовательно, максимальная ошибка округления составит 5 единиц ближайшего отброшенного результата.
3.7 Оценка значимости изменения измеряемой величины
При выполнении предлагаемых лабораторных работ следует руководствоваться правилом: если изменение измеряемой величины превосходит утроенную среднеквадратичную погрешность, то это изменение значимо и является проявлением физико-химической закономерности. В противном случае обычно считают, что измеряемая величина изменялась под действием случайных факторов.