МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ

южно-российский государственный технический университет

(Новочеркасский политехнический институт)

Волгодонский институт

Е.С.Молошная, С.А.Шилов

электрические цепи однофазного

синусоидального тока

методические указания к лабораторным работам

по электротехнике и основам электроники

Новочеркасск 2003

УДК 621.3.024.1(076.5)

Рецензенты: канд. техн. наук., доц. О. Г. Дигун

канд. техн. наук., доц. В. А. Фролов

Научный редактор канд. техн. наук., зав.каф. электротехники и автоматики ВИ ЮРГТУ И. А. Сысоев

электрические цепи однофазного синусоидального тока: Метод. указания к лабораторным работам по электротехнике и основам электроники

/Е. С. Молошная, С. А. Шилов; Волгодонский институт ЮРГТУ. – Новочеркасск: ЮРГТУ, 2003. 23с.

Настоящие методические указания имеют цель оказать помощь студентам при самостоятельной подготовке и выполнении лабораторных исследований по курсу «Электротехника и электроника» раздел «Электрические цепи однофазного синусоидального тока».

Указания предназначены для студентов 3, 4 курсов специальностей ТМ-120100, СП-120500, КР-101300, ТС-100500, ОД-240400 дневной вечерней и заочной форм обучения.

Волгодонский институт ЮРГТУ, 2003

Е. С. Молошная, С. А. Шилов, 2003

ЛАБОРАТОРНАЯ РАБОТА № 1

Исследование линейной цепи синусоидального тока при последовательном соединении приемников.

Цель работы. Экспериментально исследовать влияния параметров электрической цепи переменного тока на значения электротехнических величин: тока, напряжения, мощности, cos φ; определить параметры цепи по результатам измерений в различных режимах; проанализировать режим резонанса напряжения.

1. Программа работы

1.1 Ознакомиться со схемой установки (рис.1.1) и измерительными приборами. Записать данные приборов и их типы в таблицу.

1.2. В цепи (рис.1.1) :

• подключить осциллограф для снятия осциллограмм входного напряжения и тока. На вход Х-Х осциллографа подать напряжение с шунта R_ш, а на вход y-y – входное напряжение;

• включить цепь тумблера F;

• настроить цепь в резонанс путем изменения индуктивности дросселя (первоначально сердечник полностью выведен), наблюдая на экране осциллографа совмещение осциллограмм входного напряжения и тока в цепи;

• снять осциллограмму тока i и напряжения u в резонансном режиме;

• измерить действующие значения входного напряжения U, тока в цепи I , напряжение на индуктивной катушке U_k и на конденсаторе U_с, активную мощность, потребляемую в цепи P;

• рассчитать коэффициент мощности цепи cosφ и фазовый угол φ.

Данные опытов и расчетов внести в таблицу.

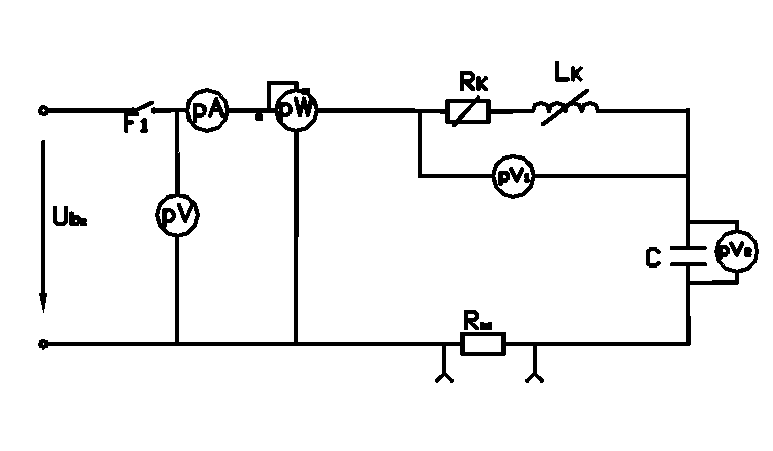
Рис. 1.1. Принципиальная схема исследуемой цепи

1.3 Расстроить резонансный режим один раз уменьшив ,а другой раз увеличив индуктивность дросселя. Снять осциллограммы и повторить все измерения и расчеты п.2.2, для этих двух режимов. Данные занести в таблицу.

1.4. Построить векторные диаграммы токов и напряжений для трех режимов φ>0; φ=0; φ<0.

Данные опытов и расчетов Таблица 1.1

№ пп.

U В

f Гц

U1 В

U2 В

I А

P Вт

cosφ

φ град

R Ом

XL Ом

XC Ом

Q BAр

S BA

Данные опытов

Результаты расчетов

1

2

3

1.5. Исследовать последовательную цепь RLC с помощью компьютерного редактора E.W.B.

2. Пояснения к работе.

Закон изменения любой синусоидально изменяющейся величины может быть записан в виде

,

где - мгновенное значение тока;

- максимальное значение (амплитуда);

- фаза;

- начальная фаза (при t=0);

- угловая частота;

f - частота, Гц.

Связь между током и напряжением для мгновенных значений на элементах R, L, C вычисляется по формулам:

;

;

.

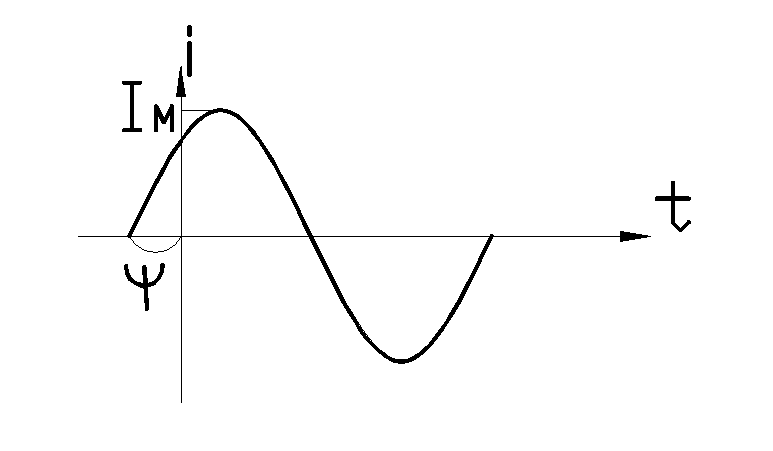
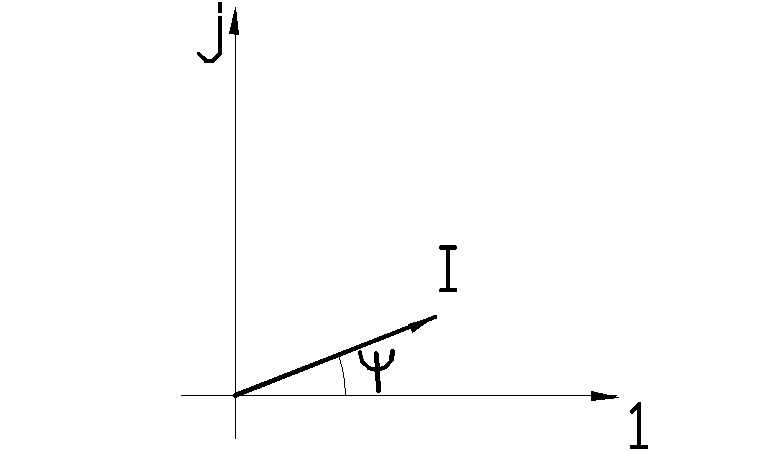
а) б)

Рис. 1.2. Временная диаграмма синусоидального тока (а) и его векторная диаграмма (б).

На схемах стрелками показывают условно положительное направление синусоидально изменяющихся величин. Стрелка означает, что именно так направлена синусоидальная величина, когда положительна в соответствии с запасом ее изменения.

Действующим называется такой не изменяющийся во времени ток, при котором в сопротивлении за время в один период выделяется то же количество теплоты, что и при постоянном токе:

; ; .

На действующее значение градуируются шкалы электромеханических измерительных приборов.

Используя метод математического моделирования можно синусоидально изменяющейся величине поставить в соответствие вращающийся вектор, позволяющий определить фазу и мгновенное значение в любой момент времени. Это позволяет перейти от дифференциальных уравнений, написанных, для мгновенных значений токов и напряжений, к алгебраическим уравнениям и значительно упрощает расчет цепей перемещения тока.

Для анализа и расчета широко используются векторные диаграммы – совокупность векторов, отображающих фазовые и количественные соотношения между электрическими величинами в данной цепи, вытекающие из законов Кирхгофа. При анализе и расчете электрических цепей переменного тока необходимо учитывать не только сопротивление различных их элементов, но также индуктивности и емкости, если, конечно, они имеют существенное значение. Объясняется это тем, что при переменном токе в устройствах, обладающих индуктивностью, возникает Э. Д. С. самоиндукции, а в устройствах, обладающих емкостью, появляется изменяющееся напряжение. Э. Д. С. самоиндукции и напряжение на емкости оказывают влияние на ток, напряжение и мощность в электрической цепи.

Рассмотрим идеализированные элементы электрических цепей переменного тока, имеющие только активное сопротивление R, индуктивность L или емкость С.

Если ток в этих элементах будет изменяться по закону , то напряжения будут описываться выражениями:

;

;

,

где

индуктивное сопротивление, Ом, .

емкостное сопротивление, Ом

Разделив левые и правые части соотношений между амплитудными значениями напряжений и токов на, получим соотношение между действующими значениями:

; ; .

Указанные выше соотношения, а также временные и векторные диаграммы имеют важнейшее значение для изучения синусоидального тока.

Мощность – это скорость изменения энергии. Можно говорить о мгновенной, активной, реактивной и полной мощности.

Мгновенная мощность равна произведению мгновенных значений тока и напряжения:

.

Мгновенная мощность изменяется с течением времени и по величине, и по знаку.

При активной нагрузке (φ=0) в течение всего периода изменения тока

р>0, в этом случае электрическая энергия потребляется из сети и обратно в сеть не возвращается. Она преобразуется в тепло, механическую энергию и т.п.

При индуктивной нагрузке (), а также при емкостной нагрузке () в одну четверть периода, когда р>0, электрическая энергия забирается из сети и преобразуется в энергию магнитного или электрического поля; в другую четверть периода, когда р<0, такое же количество энергии преобразуется в электрическую энергию и возвращается в сеть.

В электрических цепях могут быть разные по величине и по характеру сопротивления (R,X_L,X_C). В соответствии с этим угол сдвига фаз между напряжением и током может лежать в пределах .

В случае смешанной активно-индуктивной () или активно-емкостной нагрузки () забираемая из сети электрическая энергия больше энергии, возвращаемой в сеть, так как возвращается только та часть энергии, которая была преобразована в энергию магнитного или электрического поля.

Под активной мощностью понимается мощность, равная среднему значению мгновенной мощности за период

,

где cos φ –коэффициент мощности показывает, какую часть полной мощности, потребляемой приемником, составляет активная мощность.

Реактивная мощность, индуктивная или емкостная

.

Реактивная мощность соответствует энергии, которая в одну часть периода забирается из сети и преобразуется в энергию магнитного или электрического поля, а в другую - вновь преобразуется в электрическую энергию и возвращается в сеть.

Полная мощность включает в себя активную и реактивную мощность:

.

В последовательной цепи R,L,C согласно второму закону Кирхгофа в комплексной форме

.

Действующее значение входного напряжения

.

Коэффициент мощности

;

.

Мощности

;

;

.

Резонансом напряжения называется режим работы последовательной цепи R,L,C, наступающий при равенстве индуктивного и емкостного сопротивлений:

;

Как видно, резонанс может быть получен путем изменения индуктивности, емкости или частоты. Режим резонанса напряжения характеризуется следующим образом

• полное сопротивление минимально и равно активному сопротивлению :

;

• ток в цепи максимален

;

• напряжение на индуктивности и емкости равны между собой ,находятся в противофазе и могут быть по величине значительно больше входного напряжения

; ;

• активная мощность имеет максимальное значение, cosφ=1;

• реактивная мощность всей цепи равна нулю, хотя индуктивная и емкостная мощности могут иметь большие значения

.

Между индуктивностью и емкостью происходит обмен энергией, из сети реактивная энергия и соответствующая ей реактивная мощность не потребляются:

• полная мощность равна активной мощности: S=P;

• напряжение и ток совпадают по фазе: φ=0.