
- •Методы растрирования кривых второго порядка
- •1. Вывод окружности
- •1.1. Метод прямого вычисления координат
- •Void Circle_Pixel(int x0, int y0, int X, int y, int color); {
- •Void Circle (int x0, int y0, int r, int color) {
- •1.2. Алгоритм Брезенхема для вывода окружности
- •Var X,y,d:integer:
- •2. Вывод эллипса
- •2.1. Построение эллипса по неявной функции
- •2.2. Построение путем сжатия окружности
2. Вывод эллипса
Прежде всего отметим, что у эллипса, в отличие от окружности, всего 2 оси симметрии, поэтому по точкам придется строить уже 2 октанта:

2.1. Построение эллипса по неявной функции
Неявная функция, задающая эллипс, имеет вид:


Пусть f(x, y) = b2x2 + a2y2 - a2b2.
тогда,
в каждой точке
![]() эллипса
существует вектор нормали, задаваемый
градиентом функции
эллипса
существует вектор нормали, задаваемый
градиентом функции
![]() .
Дугу разобьем на две части: первая - с
углом между нормалью и горизонтальной
осью больше 45° (тангенс больше 1) и вторая
- с углом, меньшим 45° (рис.
8.9). Движение вдоль дуги будем
осуществлять в направлении по часовой
стрелке, начиная с точки (0, b).
Вдоль всей дуги координата является
монотонно убывающей функцией от х,
но в первой части она убывает медленнее,
чем растет аргумент, а во второй - быстрее.
Поэтому при построении растрового
образа в первой части будем увеличивать
x на единицу и
искать соответствующее значение y,
а во второй - сначала уменьшать значение
y на единицу и
определять соответствующее значение
x.
.
Дугу разобьем на две части: первая - с
углом между нормалью и горизонтальной
осью больше 45° (тангенс больше 1) и вторая
- с углом, меньшим 45° (рис.
8.9). Движение вдоль дуги будем
осуществлять в направлении по часовой
стрелке, начиная с точки (0, b).
Вдоль всей дуги координата является
монотонно убывающей функцией от х,
но в первой части она убывает медленнее,
чем растет аргумент, а во второй - быстрее.
Поэтому при построении растрового
образа в первой части будем увеличивать
x на единицу и
искать соответствующее значение y,
а во второй - сначала уменьшать значение
y на единицу и
определять соответствующее значение
x.
Направление нормали соответствует вектору
![]()
Отсюда
находим тангенс угла наклона вектора
нормали:
![]() .
Приравнивая его единице, получаем, что
координаты точки деления дуги на
вышеуказанные части удовлетворяют
равенству
.
Приравнивая его единице, получаем, что
координаты точки деления дуги на
вышеуказанные части удовлетворяют
равенству
![]() .
Поэтому критерием того, что мы переходим
ко второй области в целочисленных
координатах, будет соотношение
.
Поэтому критерием того, что мы переходим
ко второй области в целочисленных
координатах, будет соотношение
![]() ,
или, переходя к целочисленным операциям,
,
или, переходя к целочисленным операциям,
![]() .
.

Рис. 8.10. Схема перехода в первой и второй областях дуги эллипса
При
перемещении вдоль первого участка дуги
мы из каждой точки переходим либо по
горизонтали, либо по диагонали, и критерий
такого перехода напоминает тот, который
использовался при построении растрового
образа окружности. Находясь в точке
![]() ,
мы будем вычислять значение
,
мы будем вычислять значение
![]() .
Если это значение меньше нуля, то
дополнительная точка
.
Если это значение меньше нуля, то
дополнительная точка
![]() лежит
внутри эллипса, следовательно, ближайшая
точка растра есть
лежит
внутри эллипса, следовательно, ближайшая
точка растра есть
![]() ,
в противном случае это точка
,
в противном случае это точка
![]() (рис.
8.10а).
(рис.
8.10а).
На
втором участке дуги возможен переход
либо по диагонали, либо по вертикали,
поэтому здесь сначала значение координаты
y уменьшается на единицу, затем
вычисляется
![]() и
направление перехода выбирается
аналогично предыдущему случаю (рис.
8.10б).
и
направление перехода выбирается
аналогично предыдущему случаю (рис.
8.10б).
Остается
оптимизировать вычисление параметра
![]() ,
умножив его на 4 и представив в виде
функции координат точки. Тогда для
первой половины дуги имеем
,
умножив его на 4 и представив в виде
функции координат точки. Тогда для
первой половины дуги имеем

Для второй половины дуги получим
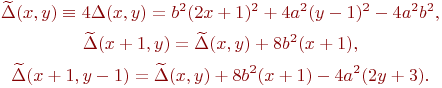
Все
оставшиеся дуги эллипса строятся
параллельно: после получения очередной
точки
![]() ,
можно инициализировать еще три точки
с координатами
,
можно инициализировать еще три точки
с координатами
![]() .
.
2.2. Построение путем сжатия окружности
Воспользуемся тем, что эллипс с параметрами a, b (пусть a > b ) получается из окружности радиуса a сжатием по оси y в a/b раз. Построим алгоритм, который является некой комбинацией алгоритмов Брезенхема для окружности и для отрезка

Начнем из точки (a, 0) на окружности и из точки (0, 0) на отрезке. Будем строить эллипс точно так же, как окружность, но смещать текущую точку по y только в том случае, когда такое смещение происходит в текущем шаге уже для отрезка, т.е. построение отрезка как раз и является реализацией сжатия в a/b раз (точнее, его дискретной аппроксимацией). Этот алгоритм тоже имеет недостаток: возможная смешанная связность полученной линии:

