Завдання 7. Перетин многоГранника площиною

Умова. Побудувати лінію перетину многогранника площиною, натуральну величину фігури перетину і розгортку.

Приклад виконання завдання наведений у додатку 8.

Мета завдання – освоєння способів побудови плоских перетинів і розгорток гранних поверхонь.

Порядок виконання завдання

1. Побудувати проекції лінії перетину многогранника із заданою площиною.

2. Визначити натуральну величину фігури перетину.

3. Побудувати розгортку многогранника й нанести на ній лінію перетину.

В індивідуальних варіантах завдання (табл. 9) як многогранники задані призми й піраміди. Для раціонального розв‘язання завдань, зазначених у пп. I, 2 доцільно використати спосіб заміни площин проекцій, що дає можливість задану площину загального положення перетворити в проектуючи положення, а фігуру перетину – у відрізок прямої. .

На рис. 5 показано, як за допомогою першої заміни площини проекцій П₂ на П₄ побудована лінія перетину площини трикутника ABC із пірамідою, а за допомогою другої заміни П₁ на П₅ визначена натуральна величина фігури перетину. Для цього через вершину С у площині трикутника ABC проведена горизонталь h. Перпендикулярно до цієї горизонталі задана замість П₂ нова вертикальна площина проекцій П₄. Лінія перетину П₁ і П₄ (вісь проекцій X₁₄) проведена перпендикулярно до h₁. Від горизонтальних проекцій вершин трикутника й піраміди перпендикулярно до нової осі проекцій X₁₄ проведені лінії зв'язку, на яких за віссю X₁₄ відкладені висотні координати зазначених вершин. У побудованій системі площин проекцій П₁ і П₄ трикутник ABC і перетин 1-4 займають проектуючи положення. Оскільки висоти точок перетину 1-4 при проектуванні на вертикальні площини П₄ і П₂ однакові, за допомогою вимірника їх легко можна "перенести" на відповідні ребра піраміди з П₄ на П₂. "Перенос" проекцій цих точок з П₄ і П₂ на П₁, виконується за допомогою ліній зв'язку.

Для визначення натуральної величини фігури перетину введена нова площина проекцій П₅. Вона задана замість першої заміни, що залишилася після, площини проекцій П₁ паралельно площині перетину. Побудови зрозумілі з рис. 5.

Розгортка піраміди виконується шляхом побудови натуральних величин усіх її граней. Для цього необхідно визначити натуральні величини всіх ребер піраміди. Горизонтальні ребра основи проектуються на П₁ в натуральну величину. Для визначення натуральних величин бічних ребер їх потрібно повернути навколо висоти піраміди до фронтального положення. При цьому висота вершин перетину, розташованих на бічних ребрах, не зміниться. Побудова розгорнення піраміди показана на рис.5.

Бічна поверхня призми розгортається в прямокутник, висота якого дорівнює висоті призми, а довжина – периметру її основи. Розгортка призми з нанесеною на ній лінією перетину показані в додатку 8.

Слід зазначити, що при виконанні завдання за індивідуальними варіантами із будь-якою призмою заміну площин проекцій можна не робити. В цьому випадку горизонтальна проекція перетину збігається з "виродженою" проекцією бічної поверхні призми, тому фронтальні проекції вершин перетину можна побудувати, виходячи із приналежності їхньої площини трикутника KLN. Натуральну величину перетину в цьому випадкові легко побудувати безпосередньо на розгортці способом зарубок за допомогою циркуля.

Якщо перетин призми площиною має більше від трьох вершин, то його натуральну величину, крім способу заміни площин проекцій, можна визначити способом обертання навколо лінії рівня. Таким способом визначена натуральна величина перетину в додатку 8.

Таблиця 9

Номер варіанта	Фігура	Координати точок																																			Площина
		A						B						C						D						E					F						K						L						N
		X		Y		Z		X		Y		Z		X		Y		Z		X		Y		Z		X		Y	Z		X		Y		Z		X		Y		Z		X		Y		Z		X		Y		Z
1	2	3		4		5		6		7		8		9		10		11		12		13		14		15		16	17		18		19		20		21		22		23		24		25		26		27		28		29
1	Піраміда	40		38		0		40		12		0		18		25		0																			50		34		23		20		10		40		13		37		10
2	–	34		40		0		46		18		0		22		18		0																			62		0		0		14		0		42		14		84		0
3	–	48		26		0		34		11		0		20		26		0		34		40		0													4		0		0		52		0		38		52		48		0
4	Призма	52		28		0		45		16		0		30		16		0		24		28		0		30		41	0		45		41		0		62		42		11		20		10		46		8		40		21
5	–	46		33		0		46		13		0		34		6		0		21		13		0		21		33	0		34		40		0		58		40		12		7		32		8		50		6		44
6	–	50		18		0		25		18		0		37		40		0																			65		37		27		9		35		13		15		6		44
7	–	50		24		0		36		10		0		22		24		0		36		38		0													70		0		0		18		68		0		18		0		39
8	–	50		35		0		50		15		0		30		15		0		30		35		0													62		20		35		14		52		35		19		15		7
9	–	50		24		0		36		10		0		22		24		0		36		38		0													62		20		13		54		5		44		11		46		14
10	–	56		32		0		56		18		0		42		10		0		30		18		0		30		32	0		42		40		0		70		0		0		20		0		42		20		50		0
11	Піраміда	54		25		0		46		12		0		30		12		0		22		25		0		30		38	0		46		38		0		66		48		35		44		6		42		15		27		11
12	–	45		36		0		45		14		0		23		14		0		23		36		0													62		0		0		15		0		35		42		58		0
13	Призма	45		34		0		45		18		0		32		11		0		20		18		0		20		34	0		32		41		0		60		0		0		38		65		0		13		0		60
14	–	50		26		0		28		14		0		28		39		0																			15		0		0		44		65		0.		56		0		45
15	Піраміда	54		26		0		39		11		0		24		26		0		39		41		0													63		18		30		15		46		30		21		20		9
16	–	45		34		0		45		18		0		32		11		0		20		18		0		20		34	0		32		41		0		11		0		0		50		0		35		35		65		0
17	Призма	50		35		0		50		15		0		30		15		0		30		35		0													52		24		12		10		18		15		17		46		42
18	–	52		28		0		45		16		0		30		16		0		24		28		0		30		41	0		45		41		0		65		37		27		9		35		13		15		6		44
19	Піраміда	41		34		0		28		11		0		15		34		0																			50		34		23		20		10		40		13		37		10
20	Призма	50		24		0		35		11		0		20		24		0		35		39		0													62		0		0		15		0		35		42		58		0
21	–	56		32		0		56		18		0		42		10		0		30		18		0		30		32	0		42		40		0		62		42		11		20		10		46		8		40		21
Закінчення таблиці 9
1	2	3	4		5		6		7		8		9		10		11		12		13		14		15		16			17		18		19		20		21		22		23		24		25		26		27		28		29
22	Піраміда	54	25		0		46		12		0		30		12		0		22		25		0		30		38			0		46		38		0		50		34		23		20		10		40		13		37		10
23	Призма	41	34		0		28		11		0		15		34		0																					62		0		0		14		0		42		14		84		0
24	–	52	28		0		45		16		0		30		16		0		24		28		0		30		41			0		45		41		0		4		0		0		52		0		38		52		48		0
25	–	50	24		0		35		11		0		20		24		0		35		39		0															62		20		35		14		52		35		19		15		7
26	–	46	33		0		46		13		0		34		6		0		21		13		0		21		33			0		34		40		0		65		37		27		9		35		13		15		6		44
27	–	41	34		0		28		11		0		15		34		0																					52		24		12		10		18		15		17		46		42
28	–	56	32		0		56		18		0		42		10		0		30		18		0		30		32			0		42		40		0		66		48		35		44		6		42		15		27		II
29	Піраміда	46	33		0		46		13		0		34		6		0		21		13		0		21		33			0		34		40		0		62		42		11		20		10		46		8		40		21
30	–	48	26		0		34		11		0		20		26		0		34		40		0															50		34		23		20		10		40		13		37		10

Висота всіх фігур 50-60 мм.

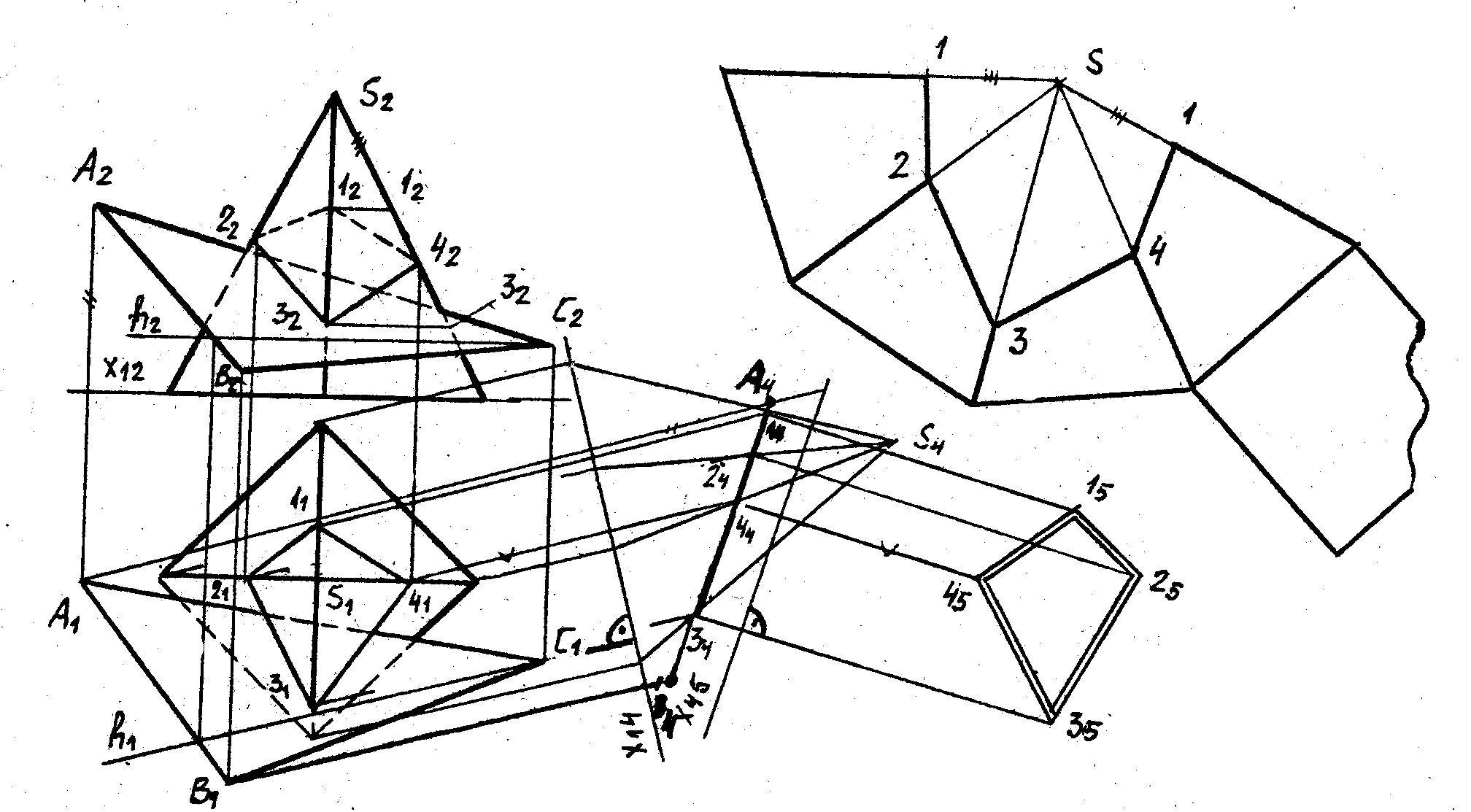
Рис 5.

Перед наведенням креслення необхідно визначити видимість площини трикутника й многогранника.