
- •Логічні операції та логічні змінні
- •2. Булеві функції
- •3. Булеві функції однієї та двох змінних
- •Практичне заняття 1
- •4. Системи базових (елементарних) операцій
- •Булеві функції багатьох змінних
- •Практичне заняття 2
- •6. Булева двохелементна алгебра. Алгебра логіки
- •Практичне заняття 3
- •7. Алгебра Жегалкіна
- •Практичне заняття 4
- •8. Диз’юнктивні нормальні форми (днф) булевих функцій
- •Практичне заняття 5
- •9. Досконала диз’юнктивна нормальна форма булевої функції
- •Практичне заняття 6
- •10. Кон’юнктивні нормальні форми (кнф) булевих функцій
- •Практичне заняття 7.
- •11. Досконала кон’юнктивна нормальна форма булевих функцій
- •Практичне заняття 8.
- •12. Принцип двоїстості
- •13. Двоїстість булевих функцій
- •Практичне заняття 9
- •14. Поліном Жегалкіна. Лінійні функції
- •Практичне заняття 10
- •15. Функції, що зберігають нуль та функції, що зберігають одиницю. Монотонні функції
- •Практичне заняття 11.
- •16. Класи Поста. Теорема Поста
- •Практичне заняття 12
- •17. Мінімізація булевих функцій
- •17.1 Постановка задачі. Основні поняття
- •17.2. Мінімізація булевих функцій методом карт Карно
- •Практичне заняття 13
- •17.3. Мінімізація на множині кнф
- •Практичне заняття 14
- •17.4. Мінімізація функцій методом Квайна – Мак-Класкі
14. Поліном Жегалкіна. Лінійні функції
Поліномом Жегалкіна називається скінчена сума за модулем 2 попарно різних елементарних кон'юнкцій.
Кількість змінних, що входять до елементарної кон'юнкції, називають рангом елементарної кон'юнкції.
Кількість попарно різних елементарних кон'юнкцій полінома Жегалкіна називають довжиною полінома.
Теорема.
Будь-яка булева функція
![]() може бути подана єдиним
поліномом Жегалкіна.
може бути подана єдиним
поліномом Жегалкіна.
Алгоритм побудови поліному Жегалкіна булевої функції, яка задана формулою алгебри Жегалкіна:
-
Розкрити дужки у заданій формулі. Для цього скористатись дистрибутивністю кон'юнкції відносно суми за модулем 2
![]()
-
Спростити вираз, використовуючи формули (1-4, п. 7).
Приклад 1.
Записати поліном Жегалкіна для імплікації
(![]() ).
).
Виконання.
![]()
![]() .
.
Приклад 2. Записати поліном Жегалкіна для еквівалентності (~).
![]()
![]() .
.
Булева функція називається лінійною, якщо вона може бути подана поліном Жегалкіна, що не містить кон'юнкцій змінних.
Приклад 3.
-
Заперечення
 – лінійна функція, оскільки її поліном
Жегалкіна
– лінійна функція, оскільки її поліном
Жегалкіна
 не містить кон'юнкцій змінних.
не містить кон'юнкцій змінних. -
Диз'юнкція
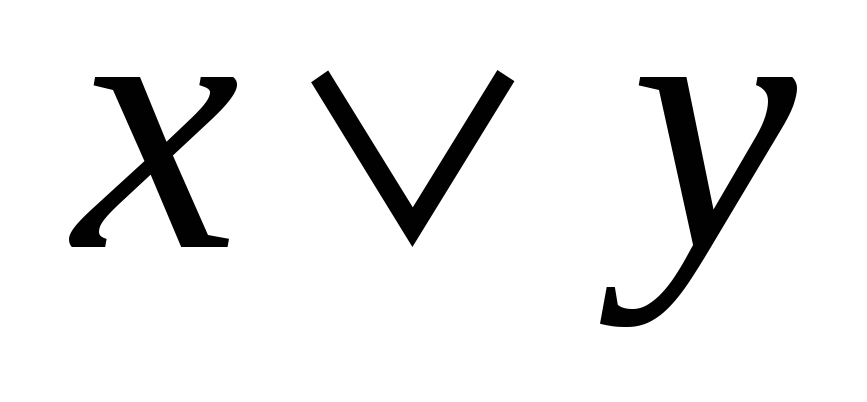 – нелінійна функція, оскільки її поліном
Жегалкіна
– нелінійна функція, оскільки її поліном
Жегалкіна
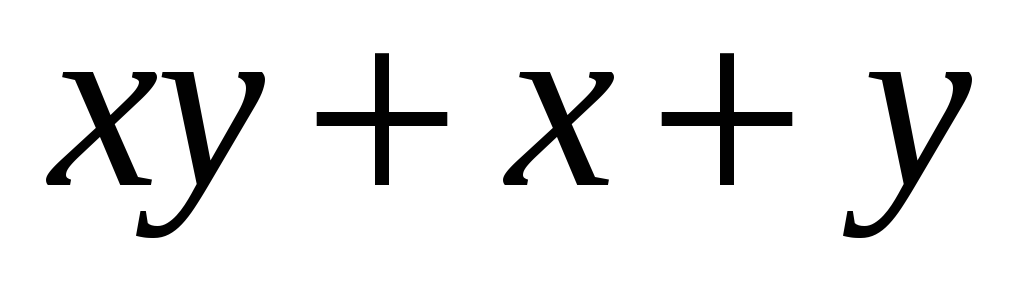 містить кон'юнкцію змінних х
і у.
містить кон'юнкцію змінних х
і у. -
Імплікація
 – нелінійна функція, оскільки її поліном
Жегалкіна
– нелінійна функція, оскільки її поліном
Жегалкіна
 (приклад 1) містить кон'юнкцію змінних
х і у.
(приклад 1) містить кон'юнкцію змінних
х і у. -
Еквівалентність
 є лінійною функцією, оскільки її поліном
Жегалкіна
є лінійною функцією, оскільки її поліном
Жегалкіна
 (приклад 2) не містить кон'юнкцій змінних.
(приклад 2) не містить кон'юнкцій змінних.
Приклад 4.
Дослідити на лінійність функцію
![]() .
.
Виконання. Побудуємо поліном Жегалкіна:
![]()
![]()
![]()
![]() .
.
Поліном Жегалкіна містить кон'юнкції змінних і тому функція
![]()
нелінійна.
Для будь-якої булевої функції існує лише один поліном Жегалкіна. Це дає можливість для його знаходження скористатись методом невизначених коефіцієнтів. Суть цього методу зрозуміла з прикладу.
Приклад 5. Побудувати поліном Жегалкіна для імплікації
![]() ,
,
використовуючи метод невизначених коефіцієнтів.
Виконання. Запишемо поліном для заданої функції у вигляді суми за модулем 2 всіх можливих елементарних кон'юнкцій змінних х і у з невизначеними коефіцієнтами:
![]() , (*)
, (*)
де коефіцієнти
![]()
![]() приймають
значення з множини
приймають
значення з множини
![]() і
визначають присутність або відсутність
елементарних кон’юнкцій у поліномі.
і
визначають присутність або відсутність
елементарних кон’юнкцій у поліномі.
Обчислимо значення функції на всіх словах з використанням (*):
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
Отже
![]() .
.
Практичне заняття 10
Вправа 1.
Записати поліном Жегалкіна для булевої
функції
![]() заданої формулою булевої алгебри.
заданої формулою булевої алгебри.
Виконання.
![]()
![]()
![]() .
.
В підсумку.
![]() .
.
Вправа 2.
Побудувати поліном Жегалкіна функції
![]() методом невизначених коефіцієнтів.
методом невизначених коефіцієнтів.
Виконання.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
В підсумку
![]() .
.
15. Функції, що зберігають нуль та функції, що зберігають одиницю. Монотонні функції
Булева функція
![]() називається функцією,
що зберігає 0, якщо на
нульовому слові вона приймає значення
0, тобто якщо
називається функцією,
що зберігає 0, якщо на
нульовому слові вона приймає значення
0, тобто якщо
![]() .
.
Булева функція
![]() називається функцією,
що зберігає 1, якщо на
одиничному слові вона приймає значення
1, тобто якщо
називається функцією,
що зберігає 1, якщо на
одиничному слові вона приймає значення
1, тобто якщо
![]() .
.![]()
Приклад 1.
Функції
![]() і
і
![]() зберігають нуль, оскільки
зберігають нуль, оскільки
![]() ,
,
![]()
Крім того, ці функції зберігають одиницю оскільки
![]() ,
,
![]()
Приклад 2. Функція
![]() зберігає 1 і не зберігає 0, оскільки
зберігає 1 і не зберігає 0, оскільки
![]() ,
,
![]()
Введемо на множині слів
відношення порядку, яке будемо позначати
символом
![]() .
Нехай
.
Нехай
![]()
і
![]()
– два слова. Тоді
![]() ,
,
якщо
![]() ,
,
![]() .
.
Якщо це не так, хоча б для
однієї пари
![]()
![]() ,
то слова
,
то слова
![]() і
і
![]() – незрівнянні.
– незрівнянні.
Приклад 3. Для функцій двох змінних є чотири слова: 00, 01, 10, 11. При цьому
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Незрівнянними є слова 01 і 10.
Булева функція
![]() називається монотонною,
якщо для будь яких слів
називається монотонною,
якщо для будь яких слів
![]() і
і
![]() для яких
для яких
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Приклад 4. Дослідити на монотонність функцію
![]() .
.
Виконання:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Висновок:
![]() – функція монотонна.
– функція монотонна.
Приклад 5. Дослідити на монотонність функцію
![]() .
.
Виконання
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Висновок:
![]() – функція не монотонна.
– функція не монотонна.
Теорема Булева функція відмінна від констант 0 та 1 є монотонна, якщо і тільки якщо вона допускає подання формулою булевої алгебри без заперечень.
Приклад 6. Визначити , чи монотонна функція
![]() .
.
Виконання.
![]()
Одержана формула булевої
алгебри не містить заперечень, отже
![]() монотонна функція.
монотонна функція.
