6. Булеві функції багатьох змінних

Булеві функції багатьох змінних () зазвичай задаються логічними формулами з заданою кількістю логічних змінних. Ці формули можна одержати суперпозицією з формул з однією або двома змінними Таблиця істинності для функцій багатьох змінних записується на основі визначення логічних операцій (0 – 11, п.1).

Приклад 1. Нехай задана функція двох змінних

.

Підставимо

, ,

у вираз для заданої функції і одержимо функцію трьох змінних

.

Побудуємо таблицю істинності цієї функції.

.

Практичне заняття 2

Вправа 1. Обчислити значення виразу

якщо .

Виконання:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. 

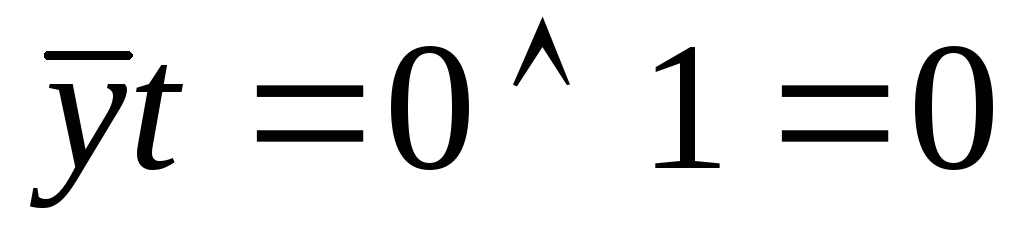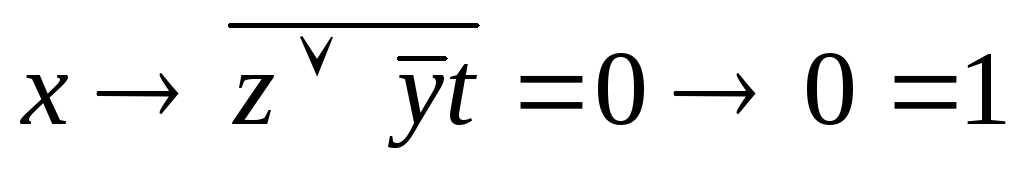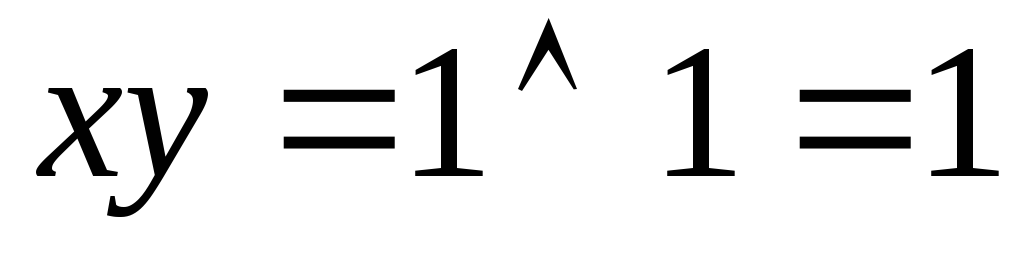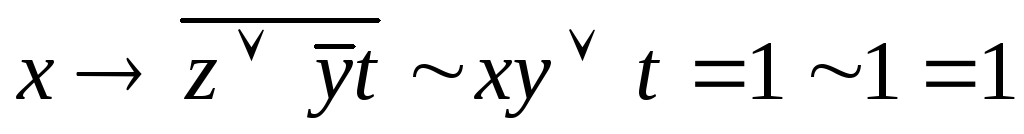8. (значення виразу)

Вправа 2. Встановити номер функції трьох змінних

.

Виконання.

.

.

Варіанти для самостійної роботи

№ в.	1 вправа. Логічний вираз, значення змінних:	2 вправа
1	, , , ,
2	, , , ,
3	, , , ,
4	, , , ,
5	, , , ,
6	, , , ,
7	, , , , ;
8	, , , ,
9	, , , ,
10	, , , ,
11	, , , ,
12	, , , ,
13	, , , ,
14	, , , ,
15	, , , ,
16	, , , ,
17	, , , ,

6. Булева двохелементна алгебра. Алгебра логіки

З визначення логічних операцій заперечення, кон’юнкції та диз’юнкції легко переконатися у таких їх властивостях.

1. Комутативність диз’юнкції та кон’юнкції:

, (1д)

. (1к)

2. Асоціативність диз’юнкції та кон’юнкції:

; (2д)

. (2к)

3. Дистрибутивність диз’юнкції відносно кон’юнкції та кон’юнкції відносно диз’юнкції:

; (3д)

. (3к)

4. Закони дій з константами:

; (4д)

; (4к)

; (5д)

. (5к)

5. Закони дій із запереченням:

;. (6д)

. (6к)

З цих властивостей можна одержати всі інші властивості операцій тотожними перетвореннями логічних формул.

6. Закони де Моргана:

; (7д)

. (7к)

7. Закони поглинання:

; (8д)

. (8к)

8. Закони ідемпотетності

; (9д)

, (9к)

які дозволяють записувати логічні формули без коефіцієнтів та показників степені.

Множина , на якій визначені операції заперечення, диз’юнкції та кон’юнкції з властивостями (1-6) називається булевою двохелементною алгеброю.

Алгеброю логіки називається двохелементна булева алгебра, доповнена операціями імплікації ()та еквівалентності (~).

Для переходу до формул булевої двохелементної алгебри (в подальшому просто булевої алгебри) необхідно скористатись рівностями:

; (10)

; (11)

; (12)

; (13)

; (14)

. (15)