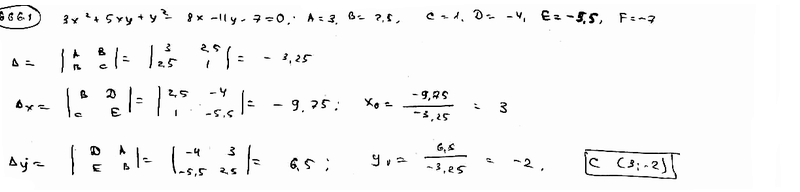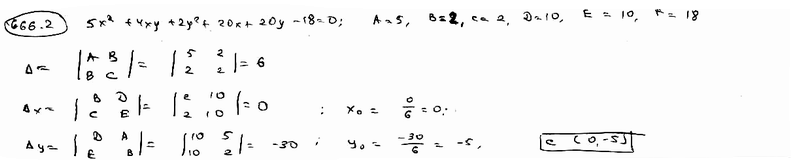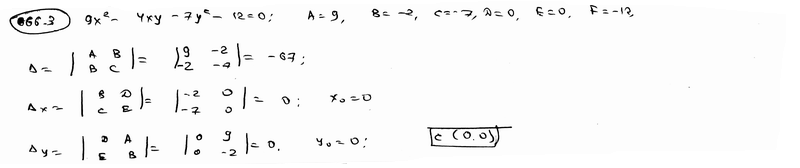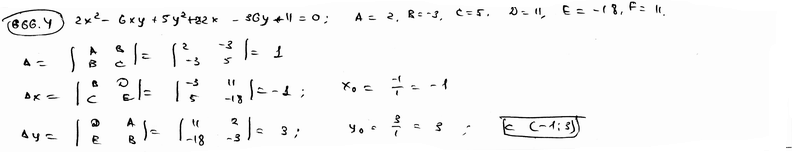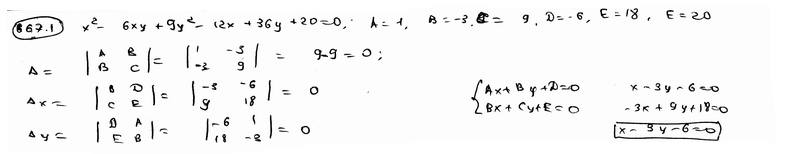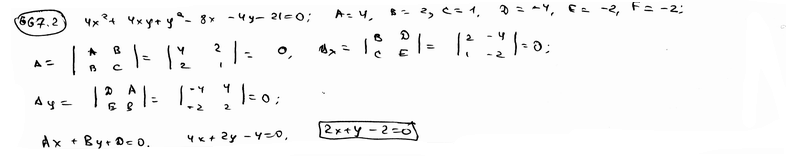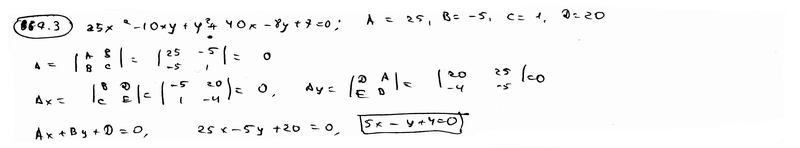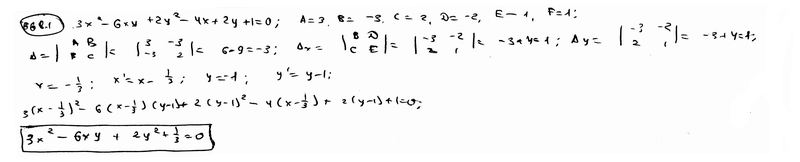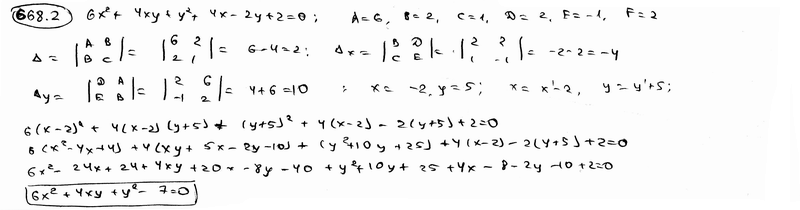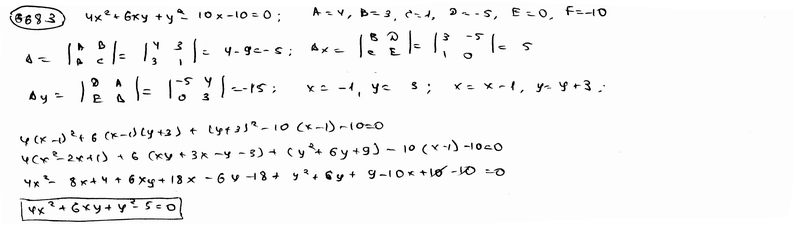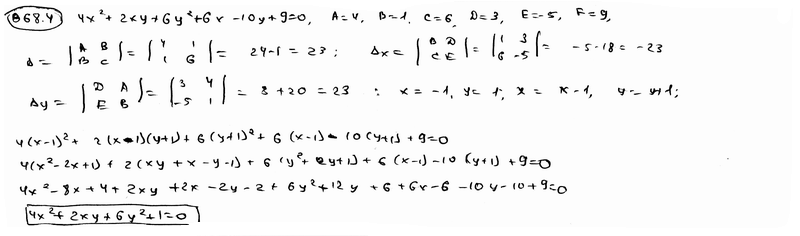- •Предисловие ко второму изданию
- •Часть 1. Аналитическая геометрия на плоскости Глава 1. Простейшие задачи аналитической геометрии на плоскости
- •Глава 1. Ось и отрезок оси. Координаты на прямой
- •Глава 2. Декартовы прямоугольные координаты на плоскости
- •Глава 3. Полярные координаты
- •Глава 4. Направленный отрезок. Проекция отрезка на произвольную ось. Проекции отрезка на координатные оси. Длина и полярный угол отрезка. Расстояние между двумя точками.
- •Глава 5. Деление отрезка в заданном отношении
- •Глава 6. Площадь треугольника
- •Глава 9. Понятие уравнения линии. Задание линии при помощи уравнения
- •Глава 10. Вывод уравнений заранее данных линий
- •Глава 11. Параметрические уравнения линии
- •Часть 3. Линии первого порядка
- •Глава 12. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых
- •Глава 13. Неполные уравнения прямой. Совместное исследование уравнений двух и трех прямых. Уравнение прямой "в отрезках"
- •Глава 14. Нормальное уравнение прямой. Расстояние от точки до прямой
- •Глава 15. Уравнение пучка прямых
- •Глава 16. Полярное уравнение прямой
- •Часть 4. Геометрические свойства линий второго порядка
- •Глава 17. Окружность
- •Глава 18. Эллипс
- •Глава 19. Гипербола
- •Глава 20. Парабола
- •Глава 21. Полярные уравнения эллипса, гиперболы и параболы
- •Глава 22. Диаметры линий второго порядка
- •Глава 5. Упрощение общего уравнения линии второго порядка. Уравнения некоторых кривых
- •Глава 23. Центр линии второго порядка
- •Глава 24. Приведение уравнения центральной линии второго порядка к простейшему виду
- •Глава 25. Приведение параболического уравнения к простейшему виду
- •Глава 26. Уравнение некоторых кривых, встречающихся в математике и ее приложениях
- •Часть 2. Аналитическая геометрия в пространстве Глава 6. Некоторые простейшие задачи аналитической геометрии в пространстве
- •Глава 27. Декартовы прямоугольные координаты в пространстве
- •Глава 28. Расстояние между двумя точками. Деление отрезка в данном отношении
- •Глава 7. Векторная алгебра
- •Глава 29. Понятие вектора. Проекция вектора
- •Глава 34. Двойное векторное произведение
- •Глава 8. Уравнение поверхности и уравнения линии
- •Глава 35. Уравнение поверхности
- •Глава 37. Уравнение цилиндрической поверхности
- •Глава 9. Уравнение плоскости. Уравнения прямой. Уравнения поверхностей второго порядка
- •Глава 38. Общее уравнение плоскости.
Глава 5. Упрощение общего уравнения линии второго порядка. Уравнения некоторых кривых
Глава 23. Центр линии второго порядка
|
665 |
|
Установить, какие из следующих линий являются центральными (т.е. имеют единственный центр), какие не имеют центра, какие имеют бесконечно много центров: |
|
|
665.1 |
|
|
|
665.2 |
|
|
|
665.3 |
|
|
|
665.4 |
|
|
|
665.5 |
|
|
|
665.6 |
|
|
|
665.7 |
|
|
|
665.8 |
|
|
666 |
|
Установить, что следующие линии являются центральными, и для каждой из них найти координаты центра: |
|
|
666.1 |
|
|
|
666.2 |
|
|
|
666.3 |
|
|
|
666.4 |
|
|
667 |
|
Установить, что каждая из следующих линий имеет бесконечно много центров; для каждой из них составить уравнение геометрического места центров: |
|
|
667.1 |
|
|
|
667.2 |
|
|
|
667.3 |
|
|
668 |
|
Установить, что следующие уравнения определяют центральные линии; преобразовать каждое из них путем переноса начала координат в центр: |
|
|
668.1 |
|
|
|
668.2 |
|
|
|
668.3 |
|
|
|
668.4 |
|
|
669 |
|
При
каких значениях m и n уравнение
|
|
|
669.1 |
центральную линию; |
|
|
669.2 |
линию без центра; |
|
|
669.3 |
линию, имеющую бесконечного много центров.
|
|
670 |
|
Дано
уравнение линии
|
|
|
670.1 |
пересекает эту линию в одной точке; |
|
|
670.2 |
касается этой линии; |
|
|
670.3 |
пересекает эту линию в двух точках; |
|
|
670.4 |
не имеет общих точек с этой линией.
|
|
671 |
|
Составить
уравнение линии второго порядка,
которая, имея центр в начале координат,
проходит через точку M(6; -2) и касается
прямая
|
|
672 |
|
Точка Р(1; -2) является центром линии второго порядка, которая проходит через точку Q(0; -3) и касается линии Ох в начале координат. Составить уравнение этой линии. |