ПРЕДИСЛОВИЕ

Содержание предлагаемой книги соответствует программе курса «Измерительные преобразователи», читаемого в высших учебных за­ведениях для специальности 0642 «Информационно-измерительная тех­ника». Современная информационно-измерительная техника распо­лагает средствами измерения около двухсот различных физических величин — электрических, магнитных, тепловых, акустических, меха­нических и т. д. Подавляющее большинство этих величин в процессе измерения преобразуется в величины электрические, как наиболее удобные для передачи, усиления, математической обработки и точ­ного измерения. Поэтому в современной измерительной технике на­ходят широкое применение преобразователи разного рода физических величин в электрические величины.

Термин «измерительный преобразователь» (ИП) употребляется в настоящее время достаточно широко и в разных смыслах. В данной книге под измерительным преобразователем понимается элементар-

HIT!' |(»ч '^{т 1}i КМГТП'Ч'РН"!."" МЧ ПГПМИС

деленного физического принципа: емкостный, магнитоупругий, пьезо-

Эттрк-тптлттргъгмй ППРП^ПЯЧОРЯТРП^ И Т П

ТТ-т-. ^-"^Т'Т' «т тпилппто ггт п? IV ОТО nori

объединенных в один конструктивный узел, выносимый на объект измерения, сохранен укоренившийся в практике термин «датчик».

Подбор излагаемого материала базируется на многолетнем опыте чтения лекций в Ленинградском политехническом институте имени М. И. Калинина.

Описать в книге небольшого объема все известные типы измери­тельных преобразователей, а также изложить вопросы теории и ме­тоды расчета этих преобразователей не представляется возможным, да и вряд ли это целесообразно. Поэтому основное внимание при на­писании книги было направлено на систематизацию физических явле­ний, положенных в основу построения преобразователей, и система­тизацию вопросов теории, используемых для их описания. В соответ­ствии с этим вопросы динамики ИП и теории погрешностей, общие для всех ИП, сосредоточены в первой и второй главах книги.

Общим элементом любых измерительных устройств, использую­щих ИП, являются измерительные цепи, связывающие ИП с после­дующей аппаратурой. Без рассмотрения измерительных цепей не пред­ставляется возможным расчет и проектирование И11. Поэтому изме­рительным цепям посвящена отдельная глава.

Существенная часть описываемых в книге преобразователей пред­назначена для измерения механических величин. Общими для пре­образователей механических величин являются упругие элементы, рассматриваемые в главе четвертой.

Остальные главы книги посвящены отдельным типам преобразо­вателей. При этом, излагая вопросы теории и расчета преобразова­телей, которые стали уже классическими (тензорезистивные, индуктив­ные, емкостные и др.), авторы рассматривают также преобразователи, получившие распространение в последние годы (пьезорезонансные, гальваномагнитные, преобразователи с использованием поверхност­ных акустических волн, магнитомодуляционные и т.д.). В то. же время некоторые широко применяемые преобразователи, достаточно подробно описанные в специальной литературе, в настоящей книге не рассматриваются (акустические, преобразователи с радиоактивным излучением, электрон но-лучевые и др.).

Авторы старались уделить больше внимания методам расчета из­мерительных преобразователей с иллюстрацией их достаточным чис­лом примеров.

В работе над рукописью и в написании некоторых глав приняли участие д-р техн. наук, профессор Дрезденского технического универ­ситета А. Лен к (гл. 4 и 5), сотрудники Ленинградского политехниче­ского института имени М. И. Калинина — канд. техн. наук, доцент С. А. Спектор (§ 8-10 и 8-11), канд. техн. наук, доцент В. С. Гут- ников (§ 7-4 и 11-5), канд. техн. наук Л. Н. Кнорринг (§ 8-12), канд. техн. наук А. В. Клементьев (§ 5-5), канд. техн. наук, доцент Омского политехнического института Ю. Н. Кликушин (гл. 12). Главы

О . 1П . ,, П Л Г".. - " -

Авторы выражают особую признательность председателю методи-

науки И ТелЬИкм РСФСР, Д-ру IfcXH. Ьй^К, профессору Е. Г. кову. явившемуся инитшятором создания курса «Измерительные пре­образователи» и введения его в учебные планы. Авторы считают своим долгом отметить, что излагаемый материал в значительной мере учитывает результаты обсуждений и дискуссий, проводимых в коллективе кафедры информационно-измерительной техники, а также обязан своим созданием лекторам, ранее работавшим над этим курсом: А. М. Туричину, М. М. Фетисову, Д. И. Зорину.

Авторы благодарны коллективу кафедры информационно-измери­тельной техники Ленинградского электротехнического института имени В. И. Ульянова (Ленина), а также д-ру техн. наук, профессору А. М. Мелик-Шахназарову за полезные замечания, сделанные ими при рецензировании рукописи настоящей книги.

Замечания и пожелания по книге просьба направлять по адресу: 191041, Ленинград, Марсово поле, 1, Ленинградское отделение Энер- гоатомиздата.

Авторы

ГЛАВА ПЕРВАЯ

ОБЩИЕ СВОЙСТВА И ВОПРОСЫ ТЕОРИИ ПОГРЕШНОСТЕЙ ' ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ

1-1. ОСНОВНЫЕ ПОНЯТИЯ и ОПРЕДЕЛЕНИЯ

Измерительное преобразование представляет собой отражение раз­мера одной физической величины размером другой физической ве­личины, функционально с ней связанной.

Применение измерительных преобразований является единствен­ным методом практического построения любых измерительных уст­ройств.

Измерительный преобразователь — это техническое устройство, построенное на определенном физическом принципе действия, выпол­няющее одно частное измерительное преобразование. Работа измери­тельных преобразователей протекает в сложных условиях, так как объект измерения — это, как правило, сложный, многогранный про_: цесс, характеризующийся множеством параметров, каждый из кото­рых действует на измерительный преобразователь совместно с осталь­ными параметрами. Нас же интересует только один параметр, кото­рый намывном тмгпчслюй ягличш-ти, я в се остальные параметры про­цесса считаем помехами, поэтому у каждию мзмери i ел ьпш и иреии- разователя целесообразно установить его естественную входную величнни кторяя лучше всего вос.щжнимаехсн им на шине полдел. Подобным образом можно выделить естественную выходную величину нреооразователя. По виду eciееiвенной ьылидний злекхричеекий ье- личины преобразователи подразделяются на две большие группы¹: генераторные (с выходной величиной е — / (х) или i = f (х) и внутрен­ним сопротивлением Z_BH = const) и параметрические (с ЭДС е — О и выходной величиной в виде изменения R, L или С в функции х).

Функция преобразования измерительного преобразователя — это функциональная зависимость выходной величины от входной, описы­ваемая аналитическим выражением или графиком. Чаще всего стре­мятся иметь линейную характеристику преобразования, т. е. прямую пропорциональность между изменением входной величины и соот­ветствующим приращением выходной величины преобразователя.

Для описания линейной характеристики преобразования а = = <р (х) == <%₀ + SAX достаточно двух параметров: начального зна­чения выходной величины а₀ (нулевого уровня), соответствующего нулевому (или какому-либо другому характерному) значению вход­ной величины х, и показателя относительного наклона характеристики 5 == Аа/Ах, называемого чувствительностью преобразователя.

Чувствительность преобразователя — это, как правило, именован­ная величина с разнообразными единицами, зависящими от природы входной и выходной величин. Для реостатного преобразователя еди­ница чувствительности — Ом/мм, для термопары — мВ/К, для фото­элемента— мкА/лм, для двигателя — об/(с-В) или Гц/В, для галь­ванометра — мм/мкА и т. д.

Чувствительность измерительного прибора, состоящего из после­довательного ряда измерительных преобразователей, определяется произведением чувствительностей всех преобразователей, образую­щих канал передачи информации. Чтобы это наглядно пояснить, ргс- смотрим прибор (рис. 1-1) для измерения и регистрации быстрых ли­нейных перемещений, состоящий из датчика, измерительного неравно­весного моста, усилителя и вибратора магнитоэлектрического осцил­лографа. Пусть датчик при воздействии на него измеряемого переме­щения 1 мм изменяет свое сопротивление на 1 % начального значения. Тогда его чувствительность 5_Д = 1 % /мм. Датчик включен в мост, который при X = 0 уравновешен. При отклонении X от 0 мост выхо-

Датчик Мост Усилитель Вибратор

Рис. 1-1

дит из равновесия, и на его выходе возникает напряжение. Если при изменении сопротивления датчика на 1 % на выходе моста появляется напряжение 10 мВ, то чувствительность моста равна 5_М = 10 мВ/%. Ruyoittoo паппяжотшс \тостя птястгя пя выхоп усилителя, и если чувствительность усилителя составляет .ь_ус = 1и мя/мь, то выходной ток усилителя, поступающий в вибратор осциллографа, будет равен JUU ма. при чувствительности виоратора «х — 1 мм,мА этот ток вы­зовет отклонение луча вибратора на 100 мм. Таким образом, резуль­тирующая чувствительность приоора оудет равна «5 = б_д5_м5_ус5_в = = 1 %/мм-10 мВ/%-10 мА/мВ-1 мм/мА = 100 мм/мм.

Понятия реальной и номинальной характеристик и погрешности измерительного преобразователя. При градуировке серии однотип­ных преобразователей оказывается, что их характеристики несколько отличаются друг от друга, занимая некоторую полосу. Поэтому в па­спорте измерительного преобразователя приводится некоторая сред­няя характеристика, называемая номинальной. Разности между но­минальной (паспортной) и реальной характеристиками преобразо­вателя рассматриваются как его погрешности.

Систематические, прогрессирующие и случайные погрешности из­мерительных преобразователей. Систематическими называются по­грешности, не изменяющиеся с течением времени или являющиеся не изменяющимися во времени функциями определенных параметров. Основное свойство систематических погрешностей состоит в том, что они могут быть почти полностью устранены введением соответст­вующих поправок.

Особая опасность постоянных систематических погрешностей за­ключается в том, что их присутствие чрезвычайно трудно обнаружить. В отличие от случайных, прогрессирующих или являющихся" функ­циями определенных параметров погрешностей постоянные система­тические погрешности внешне себя никак не проявляют и могут долгое время оставаться незамеченными. Единственный способ их обнаружения состоит в поверке нуля и чувствительности путем по­вторной аттестации прибора по образцовым мерам.

Примером второго вида систематических погрешностей служит большинство дополнительных погрешностей, являющихся не изме­няющимися во времени функциями вызывающих их влияющих вели­чин (температура, частота, напряжение и т. п.). Эти погрешности бла­годаря постоянству во времени функций влияния также могут быть скорректированы введением дополнительных корректирующих пре­образователей, воспринимающих влияющую величину и вводящих соответствующую поправку в результат преобразования основного преобр азов ател я.

Прогрессирующими называются погрешности, медленно изменяю­щиеся с течением времени. Эти погрешности, как правило, вызываются процессами старения тех или иных деталей аппаратуры (разрядка источников питания, старение резисторов, конденсаторов, деформа­ция механических деталей, усадка бумажной ленты в самопишущих приборах и т. д.). Особенностью прогрессирующих погрешностей яв­ляется то обстоятельство, что они могут быть скорректированы без выяснения вызвавших их причин введением поправки, но лишь в дан­ный момент времени, а далее вновь монотонно возрастают. Поэтому в отличие от систематических погрешностей прогрессирующие погреш­ности требуют непрерывного повторения коррекции, и тем более ча- гтого чг\» vfupo ж^ятр-гтлтп itv остатпчттог чттячошгг. Другая особен­ность прогрессирующих погрешностей состоит в том, чю с шчкм зре­ния тротш вероятностей их изменение во времени представляет собой ппппргг и wp можрт пыть описано в рамкал лиииши разработанной теории стационарных процессов.

Случайными называются неопределенные по своему значению или недостаточно изученные погрешности, в появлении различных значе­ний которых нам не удается установить какой-либо закономерности. Они определяются сложной совокупностью причин, трудно поддаю­щихся анализу. Их частные значения не могут быть предсказаны, а для всей их совокупности может быть установлена закономерность лишь для частот появления их различных значений. Присутствие слу­чайных погрешностей (в отличие от систематических) легко обнару­живается при повторных измерениях в виде некоторого разброса ре­зультатов. В подавляющем большинстве случаев процесс появления случайных погрешностей есть стационарный случайный процесс. По­этому размер случайных погрешностей характеризуют указанием за­кона распределения их вероятностей или указанием параметров этого закона, разработанных в теории вероятностей и теории инфор­мации.

Так как большинство составляющих погрешности реальных прибо­

ров проявляется именно как случайные, то их вероятностное описа­ние, а на его основе и информационное описание служат основным научным методом теории погрешностей.

Однако всегда надо !иметь в виду, что разделение погрешностей на систематические, прогрессирующие и случайные представляет собой лишь прием их анализа. В действительности же все эти три составля­ющие проявляются совместно и образуют единый нестационарный слу­чайный процесс.

1-2. ОЦЕНКИ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ (НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ)

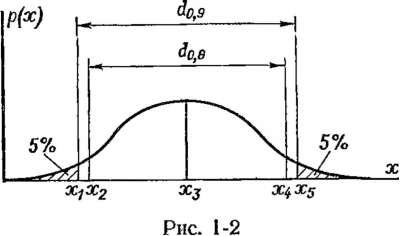
Квантильные оценки случайной погрешности. Площадь, заклю ченная под кривой плотности распределения (рис. 1-2), согласно пра­вилу нормирования, равна единице, т. е. отражает вероятность все* возможных событий. Зту площадь можно разделить на некоторые ча­сти вертикальными линиями. Аб­сциссы таких линий называются квантилями. Так, х = л^нарис. 1-2 есть 5%-ная квантиль, так как площадь под кривой р (х) слева от нее составляет 5% всей площади, а справа — 95%. Соответственно значения х2,

и х_ъ на рис. 1-2 — 10%-ная, 50%-ная, 90%-ная и 95%-ная квантили и могут быть обо­значены как х₂ = х₀,10» х₃ = *_0i50, х_й = Хо,9 и х_ъ = л:₀,95- Интер­вал значений х между y, ~ и г- v, пуратыяяст ^П0°А ьсе а возможных значении случайном величины и называется интерквантильным промежутком с 90%-ной ловепительной вепоятнп- с!ью /%. jc.1 и протяженность равна = r_c>&- — v_fiuo. Интеркрзн- тильный промежуток d₀,₈ = я₀.9 — Чл и включает в себя 80% всех возможных значений случайной величины и т. д.

На основании такого подхода вводится понятие квантильных оценок погрешности, т. е. значений погрешности с заданной довери­тельной вероятностью Р_д как границ отрезка ±Д_д = ±dj2, на про­тяжении которого встречается Р_д процентов всех значений погреш­ности, а (1 — Р_л) процентов общего числа наблюдений оказываются за границами этого интервала.

Так как квантили могут быть любыми, то при сообщении довери­тельного значения погрешности Д_д должно обязательно одновременно указываться и значение доверительной вероятности Р_д, т. е. вероят­ности того, что модуль фактической погрешности будет не больше зна­чения Д_д. Следовательно, такая оценка случайной погрешности есть указание ее «максимального» значения с заданной доверительной вероятностью.

Значения Р_д чаще всего выбираются равными 0,5; 0,8; 0,9 или 0,95. Доверительная погрешность при Р_д = 0,5 общепринята в артиллерии

и называется срединной ошибкой, доверительная вероятность Р_д = 0,8 общепринята во всех стандартах и расчетах надежности средств элект­роники, автоматики и измерительной техники, а значения Р_п = 0,9 _и р_д = 0,95 являются предпочтительными (см. § 1-6) значениями до­верительной вероятности при нормировании соответственно случайной и результирующей погрешностей средств измерений.

Достоинство доверительной погрешности состоит в том, что ее значение может быть оценено по экспериментальным данным очень простым путем. Пусть проведена серия из п измерений. Из п погреш­ностей образуют вариационный ряд, расположив их в порядке воз­растания. Слева условно приписывают значение —оо, а справа — зна­чение + оо, так что вариационный ряд —оо, Д₍₁₁, Д₍₂₎, ...,Д_1ЛЬ +оо состоит из (п + 2) членов. Индексы в скобках означают, что в вариа­ционном ряду Д₍₁₎ ^ Д₍₂₎ ^ ... ^ Д_(в). Утверждается, что" каждый из членов вариационного ряда является оценкой соответствующих квантилей, которые делят интервал (0, 1) на (п + 1) частей с равными значениями вероятностей, т. е. в среднем вероятности попадания зна­чений погрешностей в каждый из интервалов (—со, Д_с1)), (Дць Л₍₂₁), ... ..., (Д^х), А(„)), (Д₍яъ одинаковы и равны 1 !{п + 1). Следо_г

вательно, значение Д/ является оценкой ^-j-y 100%-ной квантили.

Поясним сказанное примером. Пусть при исследовании преобразо­вателя наблюдались следующие девять значений его случайной погреш­ности: -—1; 0; +2; —3; +1; +4; —2; —4; +3. После расстановки в порядке возрастания они образуют вариационный ряд —4; —3; —2; —1; 0; +1; -|-2; +3; +4. Эти наблюдения и являются оценками соот­ветствующих квантилей, так как мы вынуждены считать, что при даль­нейшем продолжении наблюдений вероятность P_f попадания их в ка-

М II I "

, , j, Ч ' /> V -/> \

(+4, +оо) одинакова и равна 1/(п + 1), поскольку полученные на-

— ■ ■ ; ' ') рв^. ов [п наше:., ^г/ч^е

I \ I — 10 и ссрилlnu^-in Ь ftd/КДЫИ ИЗ интервалов ti =

= \ Нп А- I) = О 1 = Щ0/_о)

Естественно, на практике распределение отдельных наблюдений будет не столь равномерным, как в нашем примере. Так, наблюдения «—2» могут встретиться два раза, а «—1» — ни разу и т. д. Однако при п = 9 крайние из наблюдений (в нашем примере —4 и +4) всегда будут охватывать 8 интервалов из 10 возможных. Поэтому указание, что погрешность данного преобразователя не более Д = =Ь4 должно сопровождаться добавлением «с доверительной вероятностью Р_д = = 0,8», так как в 0,2 всех случаев погрешность может попасть в ин­тервалы (—со, —4) и (+4, +оо), т. е. оказаться за пределами Д = = ±4. При п = 19 наибольшее Д_(/1) и наименьшее Д_(х) значения дают оценки 95%-ной и 5%-ной квантилей, а половина их разности — оценку доверительной погрешности при Р_д = 0,9. Если при n = 19 отбросить крайние значения Д₍*> и А_{1) и взять половину разности крайних членов Д₍,_;_1) и Д₍₂₎ оставшегося ряда, то получится оценка доверительной погрешности при Р_д = 0,8 и т. д.

Таким образом, практическое определение Д_д сводится к тому, что

из результатов наблюдений отбрасываются интервалы, ограничен­ные наибольшими по модулю, а следовательно, самыми неустойчивыми, близкими к промахам наблюдениями. Если при переменном п отбра­сывается одна и та же часть всех интервалов, например 10%, то опре­деляемое значение Д_д не зависит от длины п серии наблюдений и ока­зывается тем более устойчивым, чем больше серия наблюдений.

При этом следует иметь в виду, что по ограниченным эксперимен­тальным данным мы получаем не точные доверительные значения, а лишь приближенные значения — оценки. Достоверность квантиль- ных оценок резко повышается с понижением значения Р_д, а при по­стоянном Р_д — с ростом числа наблюдений п. Поэтому квантильные оценки с большими доверительными вероятностями могут быть найдены

только при большом числе наблюдений.

Действительно, так как вариацион­ный ряд из (п + 2) членов определяет (п + 1) интервалов с одинаковой в сред­нем вероятностью попадания в них на­блюдений, то при отбрасывании лишь членов и —со может быть опреде­лена доверительная вероятность, неболь­шая

Р ,

/1+1 *

однако достоверность оценки Д_д, найден­ной таким образом, очень мала. Для оп­ределения оценки с большей достовер­ностью с каждого конца вариационного ряда_ч должно быть отброшено некоторое число наблюдений. Располагая рядом из п наблюдений и отбрасывая с каждого из концов ряда по п_отб наблюдений, можно определить Д_д с доверительной вероятностью, не большей

р - п— 1—2п_отб Д ^ п+1

Таблица 1-1

	Необходимое п при
р
	лотб=°	"отб = 1	%тб=2
0,8	10	20	30
0,9	20	40	60
0,95	40	80	120
0,99	200	400	600
0,995	400	800	1200
0,997	667	1334	2000

Отсюда число наблюдений я, необходимое для определения Д_д с за­данной вероятностью Р_д, составляет

2(1+"отб)

1 -Р_П

1+Р_д+2/г_отб

1-Я*

и для различных значений Р_д и п_отб дано в табл. 1-1. Из таблицы ясно, что практически можно определить значения Д_д лишь с дове­рительной вероятностью Р_д ^ 0,95 (п ~ 100), а определение Д_д с Р_д = 0,99 или 0,997 трудно осуществить (необходимо п = 200

-г- 2000).

Тем не менее очень часто доверительные погрешности рассчиты­вают, вводя ничем не обоснованное предположение о том, что вид закона распределения погрешностей будто бы точно известен. В част­ности, используют прием, заключающийся в вычислении по неболь­шой серии наблюдений (2Э—30) среднего квадратического отклоне-

ння <7, а затем указывают «максимальную» погрешность А_д = За с доверительной вероятностью Р_а — 0,997 на основании предположе­ния о нормальном законе распределения.

Из приведенного выше анализа ясно, что такой прием является «научно» замаскированным обманом вне зависимости от того, допу­скается ли он сознательно или неосознанно. Дело заключается в том, что реальные законы распределения погрешностей приборов весьма разнообразны и часто очень далеки от нормального. (Это далее будет рассмотрено.) Для установления действительного хода кривой распре­деления на ее краях необходимо проведение испытаний, число кото­рых должно быть тем больше, чем большим выбирается значение доверительной вероятности (см. табл. 1-1). При малом числе испыта­ний (20—30) какие-либо сведения о ходе кривой в районе квантилей, соответствующих Р_л = 0,95 ч- 0,99 (не говоря уже о Р_д = 0,997), отсутствуют и утверждения о ходе кривой распределения в этом неис­следованном районе лишены оснований.

Основным недостатком оценки погрешности доверительным значе­нием Д_д при произвольно выбираемых Р_д является невозможность суммирования Д_д.

Среднее квадратическое значение о случайной величины X — это ее действующее (эффективное) значение, подобное действующему (в энергетическом смысле) значению тока г (£) со сложной формой кривой!

5 (x-X)^Ip(x)dx,

—со

где D—дисперсия, или второй центральный момент, случайной ве* личины, а р (х) — плотность распределения.

Основным достоинством оценки случайных величин их действую­щим (т. е. средним квадратическим) значением а является возмож­ность определения действующего значения суммы статистически неза­висимых величин как

гг п

Dz = 2 Di или oi - 2

L=l i =1

безотносительно к разнообразию законов распределения каждой из суммируемых величин и деформации законов при образовании компо­зиций *.

Энтропийное значение случайной величины. Анализ дезинформа­ционного действия случайных помех с различными законами распре­деления вероятностей привел К. Шеннона к выводу, что вносимая по­мехой дезинформация определяется не только мощностью этой по­мехи, т. е. ее средним квадратическим значением а, но еще зависит и от вида закона .распределения этой помехи.

Это положение К. Шеннон сформулировал в виде своей 16-й тео­ремы, которая утверждает, что если помеха в вероятностном смысле не зависит от сигнала, то независимо от закона распределения и мощ­ности сигнала дезинформационное действие помехи определяется ее энтропией

+со

Н(Х) = — J р (х) In р (х) dx.

—оэ

Согласно К. Шеннону количество информации / определяется как разность энтропий / = Н (X) — Н (Х/Х_п) — энтропии Н (X) значе­ний измеряемой величины до измерения и энтропии Н (Х/Х_п) неопре­деленности действительного значения X в интервале неопределенности вокруг полученного после измерения показания Х_п, т. е. энтропии погрешности. Например, при равномерном распределении измеряе­мой величины в пределах от Х_г до Х₂ и равномерном распределении погрешности в интервале неопределенности d = 2А энтропия Н (X) = = In (Х₂ — Х^, а энтропия Н (XIX_п) — In d = In 2Д и количество информации

7 = In (y,-Xi)-lnd=ln ^X2~^Xl = \nN.

Последнее соотношение / — In /V, если N = (Х₂ — XJ/d,, спра­ведливо при любом законе распределения вероятностей погрешности. Поэтому В. И. Рабинович и М. П. Цапенко предложили называть число N числом эквивалентных делений, различимых в диапазоне Х₂ — Х_г при данном законе р (х) распределения погрешности, a d₃ — эквивалентным (в энтропийном смысле) делением. Мы же будем назы­вать N числом различимых градаций измеряемой величины, a d₃ — эквивалентным (по энтропии) интервалом неопределенности. Значе­ние эквивалентного интервала неопределенности можно математи­чески строго определить для любого закона распределения как вели­чину, стоящую под знаком логарифма в выражении для Н (Х/Х_п).

При практическом использовании приведенных соотношений удоб­нее оперировать с половиной интервала d₃, именуемой энтропийным значением погрешности А_э. Формальным определением энтропийного значения погрешности являются соотношения:

Н (Х/Х_п) — In — In 2Д_Э; d₃ = 2Д_Э=е^И_и

Отношение энтропийного значения Д_э случайной величины к ее среднему квадратическому значению о называется энтропийным коэф­фициентом k = Д_э/а, несколько изменяющимся в зависимости от вида закона распределения. Так, для равномерного закона распреде­ления Д_э ⁼⁼ ~[/~Зо — 1,73о и k ^z= 1,73, для симметричного экспонен­циального распределения k = 1,92, для треугольного закона (распре­деление Симпсона) k — УЗе/2 = 2,02 и для нормального распределе­ния k = Упё/2 ~ 2,066 ~ 2,07.

Практически используемая оценка погрешности в виде максималь­ного значения из серии 20—30 наблюдений наиболее близка именно к.энтропийному значению погрешности, так как Л_э = А_д для симмет­ричного экспоненциального распределения при Р_д — 0,935, для нор­мального распределения — при Р_д =^0,961 и для равномерного рас­пределения — при Р_д = 1.

Использование энтропийного значения погрешности А_э и энтро­пийного коэффициента k закона распределения позволяет получить простую и строгую связь мощности помехи о² с вносимой ею дезинфор­мацией Н (Х/Х_п) или с получаемым при измерении количеством ин­формации / в виде

Д_э — ko\ Н (Х/Х_п) = In d₃ = In 2kc\ N = (X₂ - X_x)l(2ko)\ I — \nN.

1-3. ОПРЕДЕЛЕНИЕ ОЦЕНОК СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ ПО ЭКСПЕРИМЕНТАЛЬНЫМ ДАННЫМ (НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ СТАТИСТИКИ)

Полный набор всех значений (в том числе и совпадающих между собой), которые может принять случайная величина при бесконеч­ном числе испытаний, в статистике принято называть генеральной со­вокупностью. Проводя эксперимент, получаем лишь некоторое число п этих значений, называемое выборкой объема п. Определяя по данным этой выборки характеристики закона распределения, получаем не истинные значения дисперсии D, среднего квадратического отклоне­ния (с. к. о.) а, контрэксцесса к и т. д., характерные для всей гене­ральной совокупности, а лишь некоторые, случайно отклоняющиеся от истинных значения D*, а*, х*, называемые в статистике оценками соответствующих характеристик, найденными по выборке.

Особенность экспериментально полученных значений случайной величины состоит в том, что они оказываются естественно квантован­ными (округленными). Поэтому, даже произведя п—>■ оо наблюдений, мы не сможем построить по этим экспериментальным данным плав­ные кривые функции распределения F (я) или плотности р (х), а полу­чим график р (х) лишь в виде столбцов, называемый гистограммой. К этому же приводит объединение (группирование) более мелко кван­тованных экспериментальных значений в более крупные с целью упро­щения вычислений, когда для последующих вычислений за X_t для всего столбца принимается координата центра столбца.

Число т интервалов группирования должно выбираться исходя из имеющегося объема п выборки экспериментальных данных с уче­том эксцесса (е = р₄/а⁴) распределения. Оптимальное значение т

определяется соотношением т = п°Л (или приближенно

соотношением т — lg , где х = 1/]/е), с округлением до ближай­шего большего нечетного числа.

Трудность использования этого соотношения заключается в том, что оптимальное число столбцов гистограммы необходимо выбрать в начале обработки, когда еще не известен вид распределения и оценка контрэксцесса к. Выход из этого положения состоит в использовании того обстоятельства, что значения контрэксцесса к распределений погрешностей, как правило, находятся в пределах от 0,4 до 0,7. Поэтому следует выбирать т нечетным в пределах

0,55n°'⁴<m<l,25n⁰'⁴. (1-1)

При большем числе столбцов в гистограмме получается много про­валов, а при меньшем — искажается вид распределения.

Оценка математического ожидания М (X) случайной величины есть среднее арифметическое X всех полученных результатов наблю­дений. Разброс X относительно М (X) при объеме выборки п оцени­вается значением дисперсии X, которая равна D (X) = D (х/)/п, и о (X) — о (х/)/]/д, где D (я,-) и о (х,) — дисперсия и с. к. о. генераль­ной совокупности Xi.

Оценка дисперсии D* (х/), т. е. второго центрального момента, вычисленная по определению как

п

D* (x_t) = tf (*,) = 1 ^ ■~ X)\ (1-2)

¹

оказывается смещенной. Это значит, что кроме разброса она имеет систематическую (в данном случае отрицательную) погрешность, воз­растающую в среднем по мере уменьшения п. Для исключения этой погрешности значение D* (х*), найденное по выражению (1-2), необ­ходимо умножить на. поправочный множитель Бесселя А = п/(п — 1). Поэтому под выборочной дисперсией с поправкой Бесселя понимают величину

п т

53 (й-*)»/*

^D,W° ' n-i ~^J—s=i—• <^l"³>

а под оценкой среднего квадратического отклонения с* (х/) с поправ­кой Бесселя — корень из этой величины.

Дисперсия значения дисперсии, найденной по выборке, зависит от вида закона распределения генеральной совокупности x-_L и от объема -выборки п как

где = а² и р₄ — второй и четвертый центральные моменты гене­ральной совокупности. Это соотношение при п 8 приводит к при­ближенным соотношениям:

„ « j/".-i 1,

^{V 7} п ^V ' 2a/п 2 ]Лх Г и²

где к — контрэксцесс распределения.

Для практического определения D (D*) и о (а*) приходится поль­зоваться оценками а* и [я|, хотя они тем менее достоверны, чем меньше объем выборки.

Относительная случайная погрешность определения оценки о* равна

' о* 2Vn Г у?

2Уп

т. е. не зависит от а, и поэтому не может быть уменьшена использо­ванием для измерений более точной аппаратуры, а определяется только объемом выборки (п) и видом распределения (к). Для определения оценки а*, например, с относительной погрешностью у (а*) = 0,1 = = 10% при равномерном распределении (контрэксцесс к = 0,74) достаточно п = 20, при нормальном (к = 0,577) нужно п = 50, а при экспоненциальном распределении (к — 0,408) необходимо уже п — = 125 наблюдений.

Оценка четвертого центрального момента может быть определена (без поправки на смещение) как

иг

Относительная погрешность оценки контрэксцесса к, найденной как к = а²/]/р-₄ по выборке объемом /г, приближенно (с погрешностью 10—20%) для распределений с к = 0,4 0,75 равна

/ у^d м У ¹)

Отсюда для определения оценки к с относительной погрешностью у (к*) = 0,1 = 10% при равномерном распределении достаточно п = 11, при нормальном нужно п = 73, а при экспоненциальном рас­пределении необходимо уже п = 757 наблюдений.

т _£

Оценка энтропийного значения случайной величины по экспери­ментальным данным находится согласно соотношению

dVn^i

" Г~т

^{4=1 9}1/П (".•)"'

— — VV.ign.

_d п i t

= ^10 ¹ . (1-4)

Дисперсия оценки энтропийного значения случайной величины, так же как и дисперсия о*, убывает с увеличением объема выборки п. Но уменьшение разброса с возрастанием п для Д_э происходит значи­тельно быстрее, чем для а. Поэтому если при п = 15 относительные средние квадрэтические погрешности о (ст*)/М (а*) и а (А%)/М (Д|) примерно одинаковы, то при определении этих оценок с большей точ­

ностью (например, с погрешностью 7,5% длй равномерного распре­деления) для нахождения значения о необходимо п = 30 наблюде­ний, а для вычисления Л_э с той же относительной погрешностью (7,5%) достаточен объем выборки п = 20 наблюдений.

Правильное округление результатов расчета оценок параметров распределения погрешностей особенно важно при использовании ЭВМ или электронного калькулятора, так как машина выдает их с заранее заданной разрядностью (5 или 9 десятичных знаков) и они гипнотизи­руют своей кажущейся точностью. Однако исходными данными, как правило, являются или малая выборка наблюдений, или нормируемые значения погрешностей с одной-двумя значащими цифрами. Поэтому при любых расчетах следует всегда находить погрешности полученной оценки и оставлять в округленном результате лишь 1—2 недостовер­ных десятичных- знака. Однако при оценке погрешности может ока­заться недостоверной даже первая значащая цифра. В этом случае приходится учитывать следующее обстоятельство. Если первая зна­чащая цифра есть 1 или 2, то отбрасывание второго десятичного знака приводит к слишком большой ошибке (до 30—50%). Но если первая значащая цифра, например, 9, то сохранение второго знака (т. е. ука­зание оценки, например, в виде 0,94 вместо 0,9) является дезинформа­цией, так как исходные данные не обеспечивают такой достоверности.

Исходя из этого на практике установилось следующее правило. Если первая недостоверная цифра есть 1 или 2, то сохраняется и вто­рой недостоверный знак; если же она 3 и более, то второй недостовер­ный знак опускается. В соответствии с этим правилом установлены и нормируемые значения погрешностей средств измерений: в числах 1,5 и 2,5% указываются два десятичных знака, но в числах 0,5; 4; 6% — лишь один знак.

Изложенные правила округления можно сформулировать следую­щим образом.

1. Округление любого результата расчета или измерения должно производиться в соответствии с его погрешностью, для чего одновре­менно с самим результатом должна быть оценена и его погрешность.

2. Результат округляется до того же десятичного знака, которым оканчивается округленное значение его абсолютной погрешности.

3. Если в полученной оценке недостоверна даже первая значащая цифра, то оценка указывается с двумя знаками, если первый из них есть 1 или 2, и с одним десятичным знаком, если он есть 3 или более,

4. Округление производится лишь в окончательном ответе, а все предварительные расчеты выполняются не менее чем с одним лишним знаком.

Пример. Пусть на ЭВМ было получено X = 456,78; о (X) = 1,4768 и а (а) = = 0,47118. Решение: Д₀₎₉ (а) = 1,6 о (о)_ = 1,6-0,47118 = 0,75389 « 0,8 (так как 7 > 2). Отсюда следует, что значение о (X) находится в пределах от 1,5 — 0,8= 0,7 до 1,5+ 0,8= 2,3, т. е. в значении а (X) = 1,5 оба знака недостоверны, однако оба должны быть сохранены. Погрешность оценки X равна Д_{0 9} (Х) = 1,6 о (Х) = = 1,6-1,4768= 2,36288 ~ 2,4, и X заключено в пределах от 456,8 — 2,4= 454,4 До 456,8 + 2,4 = 459,2, т. е. в оценке X достоверны лишь первые два знака. По­этому окончательно результаты должны быть представлены как X = 456,6 =Ь 2,4;

(X) = 1,5 ± 0,8 и о (с) = 0,5.

В заключение необходимо отметить, что наряду с записью резуль­тата в виде, например, о = 1,5 ±0,8 очень полезно представить его в виде 0,7 С о С 2,3. Дело в том, что первый вид записи маскирует интервал неопределенности и создает ложное впечатление благополу­чия, тогда как второй вид записи подчеркивает протяженность интер­вала неопределенности.

1-4. РАЗНОВИДНОСТИ АНАЛИТИЧЕСКОГО ОПИСАНИЯ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ПОГРЕШНОСТИ

Как было указано выше, знание вида закона распределения важно при экспериментальном определении размера случайных погрешно­стей, так как при одних распределениях достаточна выборка, состоя­щая из 10—20 наблюдений, тогда как при других оказывается недо­статочным и п = 100 ч- 500 наблюдений. Выбор вида распределения для каждой из составляющих погрешности нужен и при расчетном суммировании погрешностей при проектировании средств измерений (см. § 1-6). ГОСТ 8.011—72 предусматривает указание вида закона распределения при сообщении погрешности результатов измерений. Поэтому необходимо знать, какие виды законов распределения могут встретиться при рассмотрении случайных погрешностей, какие из них близки друг к другу и при необходимости могут быть заменены один другим, а какие, наоборот, резко отличаются друг от друга.

По признаку симметрии законы распределения подразделяются на симметричные, когда случайные погрешности, равные по значению, но различные по знаку, встречаются одинаково часто, и несимметрич­ные — скошенные. Погрешности, как правило, распределены при­близительно симметрично. По числу максимумов в кривой распределе­ния (называемых модами) законы распределения погрешностей под­разделяются на безмодальные (не имеющие мода), одномодальные и двухмодальные. С позиций теории вероятностей форма закона рас­пределения численно характеризуется его относительным четвертым моментом или его обратной величиной в виде контрэксцесса к = = сг²/]/^, а с позиций теории информации — значением энтропий­ного коэффициента k = Д_э/а. Поэтому топографическую классифика­цию законов распределения удобно, производить в плоскости этих двух координат.

Для всех возможных законов распределения к изменяется от 0 До 1, a k — от 0 до 2,066, поэтому каждый закон может характеризо­ваться некоторой точкой с определенной долготой и широтой в пря­моугольнике, представленном на рис. 1-3. Фактические законы рас­пределения погрешностей занимают на рис. 1-3 область, очерченную штриховым овалом. Для суждения о том, какими математическими выражениями эти законы могут быть аппроксимированы, рассмотрим ряд законов распределения, описываемых простейшими математиче­скими зависимостями.

Экстремальные законы распределения — это дискретное двузнач­ное распределение и семейство законов распределения Стьюдента.

Рис. 1-3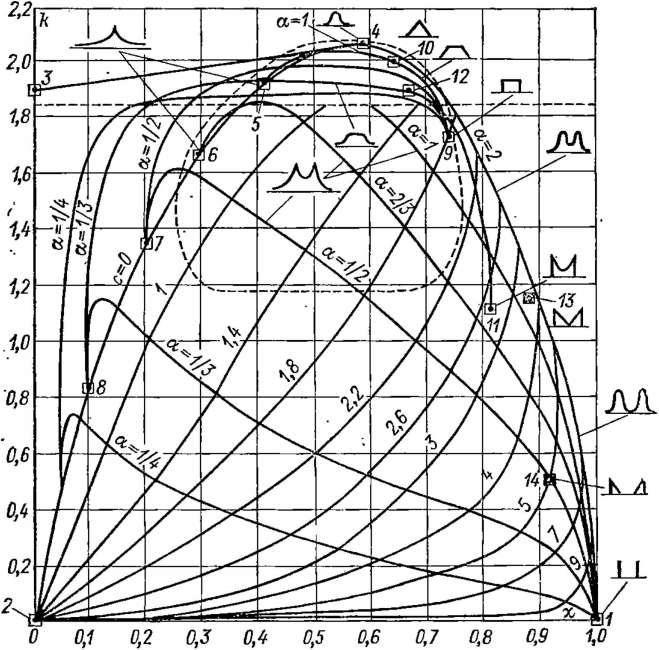

вида р(х) + 6 (—в)

двух 6-функций при х = а и

Дискретное двузначное распределение показано на рис. 1-4, а и состоит из

х = —а, под каждой из которых заключена площадь, т. е. вероятность — = 0,5. Это такое распределение, когда наблюдаются лишь равновероятные погрешности +а и —а.

Рис. 1-4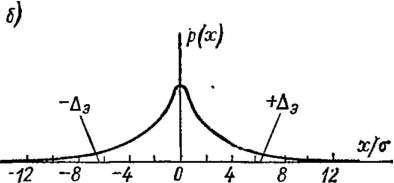

Такое распределение легко оценивается вероятностными крите­риями, для него о = a, D = а², р₄ = а⁴ и к = 1. Однако его энтро­пия Я = In 2 не зависит от а, и его энтропийный коэффициент при возрастании а стремится к нулю. Поэтому соответствующая ему точ­

ка 1 на рис. 1-3 занимает крайнее правое положение с координатами k = 0 и к = 1.

Семейство законов распределения Стьюдента описывает плотность распределения значений среднего арифметического, найденного из п реализаций, случайно выбранных из нормально распределенной ге­неральной совокупности, и в центрированном и нормированном виде описывается выражением

2

где f = п — 1 — так называемое число степеней свободы, а Г (г) — гамма-фу н кци я.

Распределение Стьюдента при п = 2 (/ = 1) получает вид

PW-ЙЭ-

или в более общем случае (при т Ф 0)

где т — координата центра распределения, а а — параметр, опре­деляющий ширину распределения. Это распределение носит наимено­вание распределения Коши (рис. 1-4, б). Распределению Коши подчи­няется, например, отношение двух нормально распределенных центри­рованных величин. Экстремальность распределения Коши состоит в том, что обычный аппарат теории вероятностей не позволяет опреде­лить его параметры — интегралы, определяющие дисперсию D и четвертый момент расходятся, т. е. дают для D* и pf значения, стремящиеся к бесконечности, а их отношение в виде к = £>/]/р,₄ стремится к нулю. Интеграл же, определяющий энтропию, продол­жает сходиться, давая значение Н (X) = In (4па) и Д_э = 2зха. Таким образом, для распределений вида, показанного на рис. 1-4, б₉ могут быть использованы лишь энтропийные и доверительные оценки, в то время как а—>-оо и не имеет смысла. Вследствие сг->оо энтропий­ный коэффициент этого распределения равен нулю и соответствующая ему точка 2 на рис. 1-3 имеет координаты к = 0 и k = 0.

Для нормированных распределений Стьюдента с / ^ 4 справед­ливы соотношения:

Г--1 ГТ~ • г - ^ - 3(Д-1) . ^а - f—2' о* ~ /г —5 '

К-1/2ЕЕ. ,

Г 3 (/ — 2) ' '' 1-Зк² »

а изменение k и к в зависимости от / имеет следующий вид:

f	k
4	1,9003	0
5	1,9717	0,3333
6	2,0053	0,4082
7	2,023	0,4472
10	2,047	0,5000
со	2,066	0,57735

■ Таким образом, точки, соответствующие распределениям Стью- дента до f ^ 4, располагаются на рис. 1-3 на оси при к — 0, а при f от 4 до бесконечности — по кривой, соединяющей точки 3 и 4. При f — оо распределение Стьюдента совпадает с нормальным распреде­лением Гаусса, которому на рис. 1-3 соответствует точка 4.

Сопоставляя линию 2—3—4 с контуром штрихового овала, ограни­чивающего реально встречающиеся распределения погрешностей, ясно, что распределения Стьюдента непригодны для описания распределений погрешностей, за исключением участка с f > 10, когда они мало отли­чаются от нормального распределения,

S)

рМ

Р(^Х)

Хг

р(х)

X

Рис. 1-5

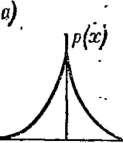
Симметричные экспоненциальные законы распределения, вид кри­вых которых изображен на рис. 1-5, могут быть описаны выражением

IX —X

Р(Х):

где

Ко 1

2ХГ (1 /а)

а а — среднее квадратическое отклонение.

Г(3/а)'

р(х)

При х = 0 и Хс — 1 выражение приводится к виду

2Г (1/а)

с нормирующим множителем А (а), зависящим от закона распределе­ния, т. е. от значения а. При оо это выражение описывает равно­мерный закон (рис. 1-5, г), при а ;> 2— плавные, близкие к трапе­цеидальным законы формы «шапо» (рис. 1-5, в), а при а = 2 — нор­мальный закон Гаусса (рис. 1-5, б) с

энтропийным коэффициентом k = 2,066 и к ~ 1/|/3 = 0,577. В коор­динатах рис. 1-3 нормальный закон характеризуется точкой 4. При а, равном 1; 2/3; 1/2; 1/3, эти законы

р(х)=-~е~ 1*1; р(х)--

имеют вид, показанный на рис. 1-5, а, и характеризуются на рис. 1-3 соответственно точками 5, 6, 7 и 8 с координатами k = 1,92; 1,64; 1,35 и 0,83 и к = 0,408; 0,286; 0,2; 0,094.

Композиции равномерного распределения с симметричными экспо­ненциальными распределениями. Равномерное распределение является безмодальным и характеризуется постоянной плотностью р (х) — = 1/(2А) в интервале от —А до +А и р (х) — 0 вне этого интервала (рис. 1-5, г). Его дисперсия D = А²/3 и о = \ D = A/j/зУ Его чет­вертый момент |л₄ = А⁴/5 и контрэксцесс к = сх²/]/^ = "[/"5/3 ^ 0,745.

Рис. 1-6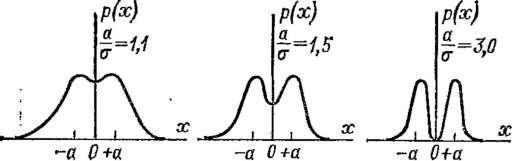

Энтропия этого распределения Н (X) — In 2А, энтропийное значение погрешности равно А и энтропийный коэффициент k = А/а = J/3 = = 1,73. Поэтому на рис. 1-3 этому распределению соответствует точ­ка 9 с координатами х = 0,745 и k — 1,73.

Композиции равномерного распределения с экспоненциальными имеют вид «шапо» (рис. 1-5, в) с различной крутизной спадов и распо­лагаются на рис. 1-3 на кривых, соединяющих точку 9 равномерного распределения с точками 4, 5, 6, 7, 6 экспоненциальных распределений. Эти кривые пересекают верхнюю часть области реальных распреде­лений, и поэтому соответствующие им композиции могут служить удобными математическими моделями для реальных распределений погрешностей с k > 1,85. Однако для распределений с k с 1,85 эти модели принципиально непригодны.

-_jje|2/3.

Композиции экспоненциальных распределений и дискретного дву­значного распределения при различных соотношениях между полу­размахом А_д = а дискретного и с. к. о. а экспоненциального распре­делений имеют вид кривых на рис. 1-6, т. е. являются двухмодальными. Геомегрическим местом точек, соответствующим этим распределениям на рис. 1-3, являются кривые, соединяющие точку соответствую- •щую дискретному двузначному распределению, с точками 4, 5, 6, 7,. 8, соответствующими экспоненциальным распределениям. Эти

кривые на рис. 1-3 помечены значениями показателя степени а соот­ветствующих экспоненциальных распределений, являющегося харак­теристикой крутизны спадов.

. Относительное содержание дискретной составляющей удобно ха­рактеризовать отношением с — а/а, называемым глубиной антимо­дальности (линии равных с также нанесены на рис. 1-3). Композиции дискретного двузначного и экспоненциальных распределений являются удобными моделями для распределений с k < 1,85.

Частные законы распределения, занимающие в отличие от рас­смотренных небольшие участки на рис. 1-3, — это трапецеидальные и арксинусоидальные распределения.

Как известно, композиция двух равномерных распределений пред­ставляет собой трапецию. Если ширина каждого из равномерных рас­пределений равна а, то трапеция превращается в треугольник (распре-

Рис. 1-7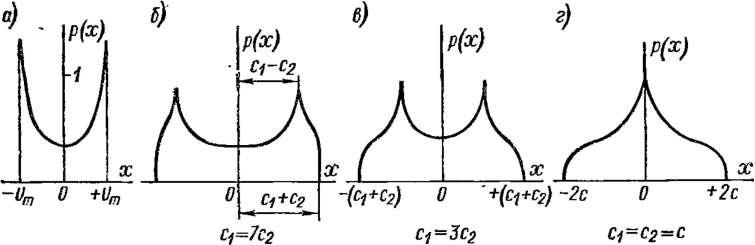

деление Симпсона). Дисперсия такого распределения D = а²/6; а — = aiYего четвертый момент щ — а⁴/15 и контрэксцесс к = 0,646; энтропия этого распределения Н (X) = In a\fe и энтропийный коэф­фициент k = У Зе/2 « 2,02.

В координатах рис. 1-3 этому распределению соответствует точка 10 с k = 2,02 и к = 0,646. Поэтому все трапецеидальные распределе­ния, являющиеся промежуточными между равномерным и треуголь­ным распределениями, располагаются на рис. 1-3 на кривой, соеди­няющей точки 9 и 10.

Согласно арксинусоидальному закону (рис. 1-7, а) распределены мгновенные значения синусоидального напряжения (например, по­меха от синусоидальной наводки на вход прибора), если считать, что моменты времени, в которые производятся отсчеты, распределены.рав­номерно по времени. При амплитуде синусоиды U_m арксинусоидаль- ное распределение записывается как

nU_m cos (arcsin ~ J siU_m j f 1 +

Среднее квадрат и чес кое (действующее) значение синусоиды обще-

2

известно и равно о == \J_ml\f2, четвертый момент щ = -Um и к ^.0,816; энтропийное значение A = ^-U_m и энтропийный коэффи­циент^ = jt/(2}/2) ~ 1,11. Поэтому на рис. 1-3 этому распределению соответствует точка 11 с k = 1,11 и к = 0,816.

При искаженной форме кривой, например при наличии небольшой составляющей в виде 3-й или 6-й гармоники,, распределение предста­вляет собой композицию двух арксинусоидальных распределений (рис. 1-7, б). В зависимости от соотношения и с₂ — ширины соста­вляющих —- оно принимает вид кривых на рис. 1-7, б, е, е. При с_х = с₂ (рис. 1-7, г) эта композиция имеет k = 1,88 и к = 0,667, т. е. харак­теризуется на рис. 1-3 точкой 12. Поэтому все промежуточные ком­позиции (рис. 1-7) располагаются на рис. 1-3 по кривой, соединяющей точки 11 и 12,

Топографическая классификация распределений (см. рис. 1-3) по­зволяет заключить, что основными разновидностями законов распре­деления случайных погрешностей являются: уплощенные распреде­ления типа «шапо», занимающие пространство между точками 5, 4, 10 и 9 на рис. 1-3 при k > 1,85, экспоненциальные (линия 6—5—4), нормальное (точка 4) и трапецеидальные (линия 10—9) распределения, располагающиеся на границе этой области, а также двухмрдальные распределения, занимающие пространство штрихового овала между точками 6 и 9 при k от 1,2 до 1,85. Что же касается распределений Стьюдента (линия 3—4) или так называемых антимодальных распре­делений с k = 1,16, к = 0,87 и k = 0,35, к = 0,92 (точки 13 и 14 на рис. 1-3), введенных ГОСТ 8.011—72, то они непригодны для опи­сания реально встречающихся распределений.

Классификация позволяет наглядно видеть близость или удален­ность законов между собой. Так, нормальный (4) и треугольный (10) законы достаточно близки, а экспоненциальные (5 или 6) и равномер­ный (9) — далеки друг от друга и т. д. И, наконец, классификация дает возможность установить вид распределения чисто формальным путем — путем вычисления на ЭВМ по экспериментальным данным оценок k и к и нанесения точки с этими координатами на график рис. 1-3.

1-5. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ОТДЕЛЬНЫХ СОСТАВЛЯЮЩИХ ПОГРЕШНОСТИ ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ

Эти законы еще мало изучены, поэтому укажем распределения лишь для тех погрешностей, для которых они известны.

Погрешность от зазора в кинематической цепи распределена по дискретному двузначному закону (см. рис. 1-4, а), так как принимает лишь значения +а и —а. Погрешность от гистерезиса в общем случае отличается от погрешности от зазора в кинематической цепи тем, что сосредоточение погрешностей вокруг +а и —а может быть более или менее размытым и распределение погрешности приобретает вид кривых на рис. 1-6.

Погрешность от наводки синусоидального напряжения распреде­лена по арксинусоидальному закону (рис. 1-7, а).

Погрешности от квантования распределены по равномерному за­кону, так как погрешностей больше + А и меньше —А не встречается, а внутри этого интервала они равновероятны. Таково же распреде­ление погрешностей и от трения — внутри зоны застоя подвижная часть может с равной вероятностью остановиться в любом положении.

Погрешность градуировки. Погрешности, допускаемые в процессе градуировки, для каждого проградуированного деления остаются' впоследствии неизменными, т. е. являются систематическими. Однако по совокупности всех делений шкалы они являются случайными, так как для различных делений могут быть как положительными, так и отрицательными и равными нулю. Распределение погрешности градуи­ровки было изучено доц. 3. Таушановым (Варна, Болгария) для при­

Рис 1.-8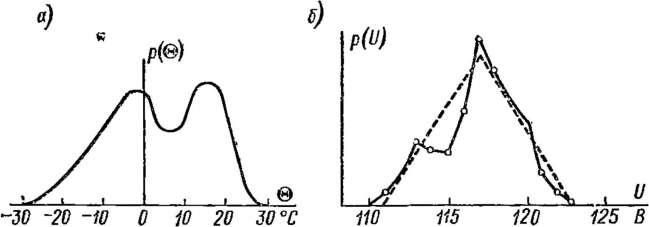

боров, изготовленных в ГДР, ЧССР, СССР и НРБ. Закон распределе­ния этих погрешностей оказался одним и тем же. Он имеег вид, пока­занный на рис. 1-5, <?, с у. ~ 0,72 и k = 1,87, что соответствует распре­делению вида

р{х)=Ае-1*1

с а = 7 или композиции равномерного и экспоненциального (с а = = 0,5) распределений с а_равн = 5а_эксп.

Распределение дополнительных погрешностей от влияющих фак­торов определяется распределением значений самого этого фактора и значением коэффициента влияния. Так как функции влияния прини­маются, как правило, линейными, а коэффициенты влияния — по­стоянными, то распределение дополнительной погрешности А как не­случайной (систематической) линейной функции случайного аргу­мента х повторяет с масштабом (по оси А = Ч'я) в виде коэффициента влияния W закон распределения вероятностей влияющей величины х.

Погрешность от температуры для приборов, работающих в цехо­вых или лабораторных условиях при односменной работе, определяется кривой циклического изменения температуры в° (t). За ночь поме­щение остывает, например, до +18 °С, а за рабочий день нагревается до +24 °С. Поэтому распределение температуры оказывается равно­мерным, например, с математическим ожиданием в = +21 °С и мак­симальным значением отклонения А — ±3 °С. Умножая эти значе­ния на соответствующий коэффициент влияния, получаем параметры распределения возникающей в этих условиях температурной погреш­ности .

При работе приборов вне помещений такое же влияние имеет рас­пределение температур атмосферного воздуха. Распределение этих температур согласно ГОСТ 16350—70 имеет вид несколько асиммет­ричной кривой (рис. 1-8, а) с двумя максимумами. Энтропийный коэф­фициент этого распределения в среднем равен k = 1,95, а энтропий­ное значение отклонений от математического ожидания для европей­ской части СССР устойчиво сохраняется равным 20 °С ±(1 -г- 2) ^СС.

Распределение погрешности от колебаний напряжения питания повторяет распределение вероятностей колебаний питающего напря­жения с учетом соответствующего коэффициента влияния. Экспери­ментально определенное распределение вероятностей значения напря­жения сети Ленэнерго приведено на рис. 1-8, б. Оно может быть при­ближенно принято треугольным.

1-6. ОСНОВЫ ТЕОРИИ СУММИРОВАНИЯ ПОГРЕШНОСТЕЙ

Задача определения расчетным путем значения результирующей погрешности по известным значениям ряда ее составляющих, назы­ваемая обычно задачей суммирования погрешностей, возникает во многих случаях практики. Так, для определения погрешности отдель­ного измерительного преобразователя необходимо найти результат суммарного действия отдельных составляющих его погрешности. Оп­ределение погрешности прибора или канала информационно-измери­тельной системы (ИИС) также сводится к определению суммарного действия погрешностей всех его преобразователей. Таким образом, задача суммирования погрешностей — это одна из основных задач как при проектировании средств измерений, так и при постановке и проведении измерений.

Трудность проведения такого суммирования заключается в том, что все составляющие погрешности в общем случае должны рассматри­ваться как случайные величины, принимающие в каждой частной реа­лизации самые разнообразные значения. С точки зрения теории ве­роятностей они могут быть описаны своими законами распределения, а их совместное действие — соответствующим многомерным законом распределения. В такой постановке эта задача практически не раз­решима уже для 3—4 составляющих (не говоря уже о 30—40 соста­вляющих), так как операции с такими многомерными законами не­преодолимо сложны. Поэтому задача состоит в том, чтобы подобрать для характеристики составляющих такие числовые оценки (напри­мер, среднее квадратическое значение, контрэксцесс, энтропийный коэффициент и т. д.), оперируя с которыми, можно было бы найти соответствующие - числовые оценки результирующей погрешности без .определения многомерных или результирующих одномерных законов распределения рассматриваемых случайных величин.

При этом необходимо учитывать следующее: а) числовые характе­ристики законов распределения составляющих (например, о и k) могут не оставаться постоянными при изменении измеряемой величины* т. е. могут изменяться в диапазоне ее изменения; Г>) отдельные соста­вляющие погрешности могут быть коррелированы между собой и в) при суммировании случайных величин законы их распределения резко деформируются.

Первое из этих обстоятельств требует разделения рассматривае­мых составляющих на аддитивные и мультипликативные, суммирова­ние которых производится раздельно для определения соответственно аддитивной и мультипликативной составляющих результирующей по­грешности.

Второе обстоятельство, т. е. возможность взаимных корреляцион­ных связей составляющих, учитывается путем использования для ха­рактеристики суммируемых составляющих погрешности их числовых оценок в виде среднего квадратического значения и коэффициентов взаимной корреляции.

Третье обстоятельство, т. е. деформация формы законов распреде­ления при суммировании случайных величин, не может быть учтено при использовании оценки погрешности в виде ее среднего квадрати­ческого значения, так как эта оценка не отражает деформации формы законов распределения. Это может быть сделано путем определения параметров формы образующейся композиции и будет рассмотрено ниже. •

Дисперсия суммы коррелированных и некоррелированных величин. Согласно теории вероятностей дисперсия суммы двух величин в об­щем случае

О (х + у) = D (х) + D (у) + 2k_Xy₉

где D (я) — дисперсия х; D (у) — дисперсия у\ k_xy — pa (я) а (у) — их взаимный корреляционный момент. Отсюда среднее квадратиче- ское значение а^ отклонения суммы этих величин от ее математиче­ского ожидания

ст₂ = + ]/^r(Tf + 2pa₁cr₂ + o'i,

где р — коэффициент корреляции. Если эти величины между собой некоррелированы, то р = 0 и = У crjf + щ.

Однако если х и у жестко и положительно (р = +1) коррелированы между собой, т. е. Ау принимает значения, лишь строго пропорцио­нальные Ая, то всякое положительное отклонение 4-Ая сопровож­дается также положительным отклонением + Ау и отклонение А (х + у) складывается как А* + А у. Это формально следует и из формулы для о₂ при р = +1, ибо а₂ = + |Лх5 + 2<т₁а₂ + al = а_х + а₂.

Если же при возрастании х значения у, наоборот, линейно убывают, то р = —1 и

<т₂ = 4- V<s\ — 2<7j02 + <*S = I tfi — a₂1.

Таким образом, оценки жестко коррелированных погрешностей (p=d=l) должны суммироваться не геометрически, а алгебраически с учетом их знаков, т. е. складываться, когда их знаки совпадают, и вычитаться, когда их знаки оказываются противоположными.

Это правило теории вероятностей в совершенно равной степени относится как к чисто случайным погрешностям, так и к систематиче­ским погрешностям, возникающим от случайного изменения влияю­щих факторов. Так, например, погрешности измерительных преобра­зователей от изменения их температуры хорошо воспроизводятся от опыта к опыту и поэтому обычно классифицируются как систематиче­ские. Однако при суммировании температурных погрешностей ряда преобразователей они могут оказаться как коррелированными, так и некоррелированными между собой и складываться как алгебраи­чески, так и геометрически.

Практические правила определения результирующей погрешности сложных измерительных устройств.

1. Для определения значения оценки результирующей погрешности всего измерительного устройства должны учитываться взаимные кор­реляционные связи различных составляющих погрешности отдельных преобразователей, поэтому исходными данными для более точного расчета должны служить значения соответствующих оценок именно отдельных составляющих, а не значение оценки суммарных погреш­ностей преобразователей.

Эти составляющие прежде всего разделяются на аддитивные и мультипликативные для их последующего раздельного суммирования.

2. Так как суммировать с учетом корреляционных связей можно лишь средние квадратические значения составляющих, то для каждой составляющей должны быть по исходным данным найдены ее средние квадратические значения.

3. Далее должны быть выделены группы сильно коррелированных между собой составляющих погрешности и внутри этих групп произ­ведено алгебраическое суммирование. К ним, как правило, относят погрешности, вызванные одной общей причиной (общий источник пи­тания, примерно одинаковые изменения температуры и т. д.), когда тесные корреляционные связи определяются логически, и для них принимают р равным +1 или —1. Погрешности же, между которыми такие взаимосвязи не обнаруживаются, относят к некоррелированным и для них принимают р = 0.

4. После того как все группы сильно коррелированных погреш­ностей выделены и внутри их произведено алгебраическое суммирова­ние, суммарные по группам и оставшиеся вне группы погрешности можно считать уже некоррелированными и складывать по правилу

Таким образом, находятся лишь средние квадратические значения аддитивной и мультипликативной составляющих результирующей пог грешности, которые не учитывают деформации законов распределения при образовании композиций, и остаются неизвестными параметры формы закона распределения результирующей погрешности.

Расчетное суммирование погрешностей с определением параметров формы образующихся композиций. Наиболее полным методом расчет­ного суммирования погрешностей является определение при сумми­ровании не только среднего квадратического значения результирую­щей погрешности, но и параметров формы образующейся композиции распределений в виде оценок значений ее контрэксцесса к и энтропий­ного коэффициента k.

Полагая распределения двух суммируемых случайных погрешно­стей симметричными и центрированными (т. е. X = 0, = 0 и \л₃ = 0), четвертый момент композиции можно найти как

ЩЕ = Н-41 + 6<TiO| + р-42.

Тогда

g| _ o}+oi ₌

р к| " к|

Таким образом, для определения контрэксцесса распределения суммарной погрешности необходимы данные о значениях контрэкс­цесса и к₂ суммируемых распределений и их с. к. о. и а₂. Следует заметить, что к^ не зависит от самих значений a_t и <х₂, а определяется лишь их соотношением. Поэтому вместо а_х и <х₂ в формулу для можно ввести относительный вес р дисперсии в суммарной диспер­сии а® + сг|:

тогда

Задача определения энтропийного коэффициента композиции не­коррелированных погрешностей по энтропийным коэффициентам и относительным весам каждой из дисперсий в суммарной дисперсии достаточно сложна. Однако в ряде опубликованных работ [10] эта задача решена для композиций всех рассмотренных выше видов за­конов распределения. Результаты этих решений удобнее всего пред­ставить в виде графиков (рис. 1-9), где по оси абсцисс отложены значе­ния р = <х|/(<т? + aj), т. е. относительный вес дисперсии <т| — вто­рого из двух суммируемых слагаемых — в суммарной дисперсии (Oi + gI), а по оси ординат — значения энтропийного коэффициента k образующейся при этом композиции.

На рис. 1-9, а кривая 1 соответствует суммированию двух по­грешностей с арксинусоидальными распределениями, кривая 2 — с арксинусомдальным и равномерным, кривая 3 — двух равномерно распределенных погрешностей, кривая 4 — с равномерным и нор­мальным и кривая 5 — „вух нормально распределенных погрешностей. На рис. 1-9, б кривые /, 2 и 3 соответствуют суммированию погреш­ностей с равномерным, треугольным и нормальным распределением с погрешностью с дискретным двузначным распределением, а кри­вые 4_У 5 и 6 — суммированию погрешности с нормальным распреде­лением соответственно с погрешностями с арксинусоидальным, равно­мерным и экспоненциальным распределением.

Несмотря на то что кривые рис. 1-9 построены только для не­скольких видов "законов распределения, их сетка настолько густа, что

позволяет на глаз интерполировать значения к для композиций лю­бых законов распределения с известным энтропийным коэффициен­том, тем более, что значения энтропийного коэффициента точнее чем до 0,1 (т. е. примерно 5%) уточнять не имеет смысла.

Суммирование доверительных значений погрешностей. Преимуще­ство доверительного значения погрешностей состоит в том, что оно в отличие от среднего квадратического (которое не существует для распределений Коши и близких к нему) и энтропийного (которое не существует для двузначного дискретного распределения и близких к нему) существует для любых законов распределений.

Основной недостаток доверительного значения погрешности со­стоит в невозможности его расчетного определения для суммы не­скольких погрешностей по известным значениям составляющих.

а)

2,2

2,066

2,0

1,8

1,73

%4

1,11 Щ

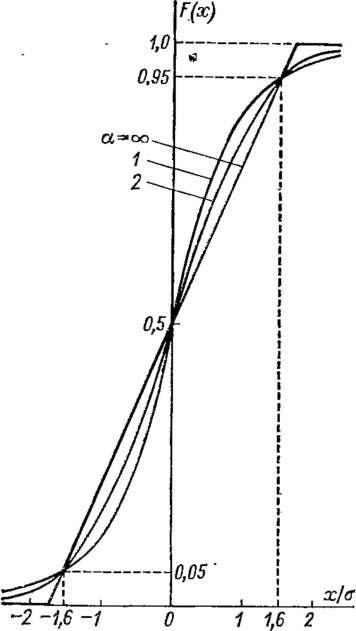
Однако из этого правила есть одно счастливое исключение. Оказы­вается, что интегральные кривые для широкого класса симметричных высокоэнтропийных (£>1,7) распределений: равномерного, тре­угольного, трапецеидальных, нормального, экспоненциальных (са^ ^ 2/3) и двухмодальных с небольшой глубиной антимодальности (с = = ahтс 1,5) — в районе 0,05-й и 0,95-й квантилей (рис. 1-10) пере­секаются между собой в очень узком интервале значений х/а = 1,6 ± ± 0,05. Поэтому с погрешностью 0,05а можно считать, что 0,05-я и 0,95-я квантили для любых из этих распределений могут быть опре­делены как

= 1,6ст и Х₀,95 = т + 1,6<т,

где т — координата центра распределения. Отсюда значение погреш­ности, определенное как A_0i9 — 1,6а, для любых из этих распределе­ний является погрешностью с 90%-ной доверительной вероятностью.

Так как при суммировании погрешностей любого сочетания рас­пределений этого класса результирующее распределение также буде| принадлежать этому классу, то и для него справедливо соотноше­ние A_0i92 = 1,6(72-

	в) 2,2
-2.0669,066
\	2,0 1/2 Ь8 ф
	1,6
I
	1,4
	V
, 1,11
0
Рис.	1-9

0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 %0 * о к \ \ / * \ 1 2 \ 3 л 4. '5 Ч \ / Р 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0				1 -Н	2 Фг	3	4	5 Л	6 1
/									к
									\ 1

1,92 1,73

\1,11

Это обстоятельство открывает возможность очень простого расчет­ного метода суммирования погрешностей. Так, если заданы значения

^ = o_s =1_и Д₀₉₂ = 1,1

* 1 = 1

Ao,9S - ]/^ Чад.

Исходя из изложенного предпочтительным значением доверитель­ной вероятности при нормировании случайных погрешностей является

Р_д = 0,9, тем более, что оценка Д_0|9 определяется с гораздо большей точ­ностью, чем, например, Л_0г97 или Д_0>99.

Р»с. МО

кие симметричные границы, как такой выход происходит а.не с обеих. В результате, если у_д = ±0,4%

Р_д = 0,9, то у_д = ±0,5% есть погрешность с доверительной ве­

роятностью Р _д = 0,95. /72 > 0,5а

Используя доверительные грани­цы ±Д_д погрешности, необходимо иметь в виду следующее обстоятель­ство. Эти границы располагаются сим­метрично относительно нуля лишь при отсутствии у прибора или преоб­разователя систематической состав- „ ляющей погрешности т. Если т Ф 0, то границы погрешности оказываются несимметричными. Так, например, ес­ли ±у_д = ±0,4%, а т = +0,1%, то одна граница оказывается равной —0,4 + 0,1 = —0,3%, а другая +0,4 + 0,1 = +0,5%. Пользовать­ся при дальнейших расчетах такими несимметричными границами погреш­ностей крайне неудобно. Поэтому на практике вместо несимметричных гра­ниц всегда указывают симметричные границы, равные по модулю большей из несимметричных, т. е. вместо «по­грешность находится в пределах от —0,3 до +0,5%» указывают «погреш­ность находится в пределах ±0,5 %». Вероятность вы хода погрешности за та- естеетвенно, в два раза меньше, так практически только с одной стороны, была определена с

Таким образом, при т ф 0, а точнее, при

До,₉₅ = ± (| т i + Д₀,₉) = ± (I т ' + 1,6а),

или просто

суммируемых составляющих Д₀₉₍-, то

т. е. результирующая погрешность Д₀,₉₅ очень просто определяется через га и оценку Д₀,₉ случайной составляющей.

В тех случаях, когда можно с уверенностью предполагать доста­точную близость закона распределения погрешностей к нормальному распределению, для определения симметричных границ доверитель­ной погрешности с доверительной вероятностью Р_д = 0,95 (при т = 0) можно использовать теоретическое соотношение для нормального рас­пределения Д₀,9б = 1,96<j.

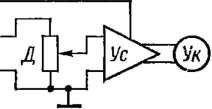
Пример расчетного определения погрешности прибора по известным погрешно­стям его отдельных преобразователей. Пусть подлежит расчетному определению погрешность прибора, выполненного по схеме рис. 1-11, по известным составляю­щим погрешностей входящих в него измерительных преобразователей. [Прибор состоит из реостатного датчика Д, усилителя Ус и указателя Ук. Реостатный дат­чик имеет аддитивную погрешность, нормированную предельным значением у_лт — = 0,15%. Датчик питается через стабилизатор Ст от общего с усилителем Ус блока питания БП. Операционный усилитель Ус предназначен для обеспечения линейной характеристики всего прибора и имеет входное сопротивление, намного большее сопротивления датчика. Выходным ука­зателем Ук служит магнитоэлектрический прибор класса 0,5.

Прежде всего, как указывалось вы­ше, все составляющие погрешности необ­ходимо подразделить на аддитивные и мультипликативные, приписать каждой из них соответствующий закон распределения и найти с. к. о. Все расчеты будем вести в относительных приведенных значениях и сохранять при промежуточных округлениях один лишний недостоверный десятичный знак в их значениях. Пусть аддитивная погрешность прибора обусловлена аддитивными погрешностями дат­чика Д и указателя У/с, а мультипликативная — колебаниями напряжений питания датчика и усилителя и зависимостью от температуры чувствительностей усилителя и указателя.

Закон распределения погрешности реостатного датчика можно принять рав­номерным, а так как чаше всего датчики нормируются без существенного запаса погрешности на старение, то у_лт = 0,15% можно считать половиной ширины рас­пределения. Отсюда с. к. о. сг_д = 'Уд_т/(/3 = 0,087%.

Погрешность электроизмерительных приборов по стандарту указывается с за­пасом на старение. Поэтому предельную погре^шность указателя можно оценить как Уук т. ~ 0,8ую где — основная погрешность, соответствующая классу точ­ности. Отсюда Тук т — 0,8*0,5 = 0,40%. Закон распределения погрешностей стрелочных электромеханических приборов близок к трапецеидальному с контр­эксцессом к = 0,7 и энтропийным коэффициентом k~ 1,9. Доверительное значе­ние погрешности сР_д= 0,9 для такого распределения равно приблизительно Y_0ig = = 0₍75Vm- Поэтому Y_{VK 0lB} = 0,75-0,40 = 0,30%. Отсюда а_ук — у_{ук 0},₉/1,6 = = 0,30/1,6— 0,188%.

Аддитивная погрешность прибора будет образована суммой двух рассмотрен­ных составляющих. Поэтому с. к. о. погрешности нуля прибора составит

а_н = ]/"^ад + ®у_К = V 0,0872 + 0,1882 = 0,207 %.

Рис. 1-11		_
Сеть	БП		Ст
		—

Равномерное распределение погрешности датчика имеет энтропийный коэффи­циент k_R~ 1,73, а для трапецеидального распределения погрешности указателя ^йук — 1,9. Для определения энтропийного коэффициента суммы этих погрешностей необходимо обратиться к рис. 1-9, б и нанести на нем кривую, выходящую при р — О из точки k — 1,73, идущую выше кривой 1 и при подходе к р= 1 сливающуюся с кривой 6. Относительный вес дисперсии трапецеидального распределения в сум­марной дисперсии составляет р = aJ_K/ff* = 0,188²/0,207* = 0,82. При этом зна­чении р нанесенная кривая проходит через значение = 2,00. Отсюда энтропий­ное значение погрешности нуля прибора составляет у_н = k_no_u — 2,00-0,207 = 0,41%.

(При этом необходимо обратить внимание читателя на то обстоятельство, что хотя кривая на рис. 1-9 проводится на глаз, т. е. весьма произвольно, ошибка определе­ния k получается ничтожной. Так, если в нашем примере вместо k_a — 2,00 при­нять = 1,98, после округления результата мы все равно получили бы у_н — = 0,41%.)

Переходя к суммированию мультипликативных составляющих погрешности, примем следующие исходные данные. Пусть коэффициент влияния температуры на чувствительность указателя равен %ук = —0,2 %/10 К и усилителя %ус — = +0,1 %/10 К. Если усилитель располагается в корпусе указателя, то оба они находятся всегда при одной и той же температуре и, следовательно, их темпера­турные погрешности достаточно жестко коррелированы между собой и должны сум­мироваться не геометрически, а алгебраически. Отсюда результирующий коэффи­циент влияния температуры равен ¥© — —0,2+ 0,1 = —0,1%/10 К. Пусть при­бор предназначен для работы в цеховых условиях при температуре от +5 до +35'°С, т. е. при температуре (20 ± 15) и все значения температур равновероятны. Тогда температурная составляющая мультипликативной погрешности имеет равномер­ное распределение с 0,1 • 15/10 = 0,15% и a_e = v_em/]/3= 0,15/^3 = 0,087%.

Пусть колебания напряжения в сети, от которой питается рассматриваемый прибор, находятся в пределах =Ь 10% н имеют треугольный закон распределения вероятности. Датчик Д питается через стабилизатор с коэффициентом стабилиза­ции k = 25. Тогда колебания напряжения питания датчика, а следовательно, и мультипликативная погрешность его выходного напряжения имеют также треуголь­ное распределение в пределах у_дт = 10/25= 0,40% с с. к. о.

= 0,40/1/6 = 0,163%.

Усилитель Ус питается нестабилизированным напряжением, но благодаря глубокой отрицательной обратной связи коэффициент влияния питающего напря­жения на коэффициент усиления усилителя снижен до значения ¥©_ус = = 0,3/[10 (Д^/t/)]. Поэтому мультипликативная погрешность прибора, вызван­ная случайными колебаниями напряжения питания, будет распределена также по треугольному закону в пределах у_{ус т} = =Ь 0,3%, с с. к. о. a_ycm =

= Yycm/K6 = 0,3]/6 = 0,122%

Так как обе погрешности от колебания напряжения вызываются одной и той же причиной, то они коррелированы между собой и складываются алгебраически, а не геометрически, хотя каждая из них случайна. Поэтому y_Um = у_{ус т} + Y_m = = 0,3 + 0,4 — 0,70% и о_и = о_{и ус} + о_ид = 0,122 + 0,163 = 0,285%. Суммар­ные погрешности от колебаний температуры и колебаний напряжения независимы и поэтому складываются геометрически, т. е. с. к. о. мультипликативной состав­ляющей a_M = |/^ra|_/ + a|_t = 1/0,2852 + 0,087² = 0,298%. Распределение суммар­ной мультипликативной составляющей есть композиция равномерного распре­деления погрешности от колебаний температуры с а_е = 0,087% и = 1,73 и тре­угольного распределения погрешности от колебаний напряжения питания с Су = = 0,285% и ky —■ 2,02. .Относительный вес дисперсии равномерно распределен­ной составляющей в суммарной дисперсии р = о^/a* = 0,087²/0,298² = 0,08- Поэтому энтропийный коэффициент этой композиции по кривым рис. 1-9, б равен йи = 2,04. И энтропийное значение мультипликативной составляющей погреш­ности равно ум = /с_ма_м = 2,04-0,298 = 0,61%.

Результирующая погрешность в конце шкалы прибора складывается из адди­тивной и мультипликативной погрешностей по правилам суммирования независимых погрешностей:

°м - 1/a^ + a^ = l/0,2072-j-0,298² = 0,36%.

Энтропийные коэффициенты суммируемых погрешностей k_u = 2,00 и — 2,04 достаточно велики, а нх с. к. о. близки между собой (о_([ — 0,207% и о_м = 0,298%), поэтому результирующее распределение достаточно близко к нормальному с £_к = — 2,066. Отсюда энтропийное значение погрешности в конце шкалы прибора равно Vk = = 2,066 • 0,36 = 0,74%.

Таким образом, при испытаниях такого прибора следует ожидать изменения погрешности от у_а = 0,41% в начале шкалы до у_к ~ 0,74% в конце шкалы. Однако при нормировании погрешности такого прибора по стандарту необходимо иметь запас на старение не менее 25% фактической погрешности, а нормируемые зна­чения погрешности в начале и конце шкалы должны быть выбраны из ряда пред­почтительных чисел, предусмотренных ГОСТ 8.401—80, т. е. должны быть ука­заны [Тн — 0,41/0,8 = 0,5% и у_к= 0,74/0,8= 1%, т.е. класс прибора указан как 1,0/0,5.

Несмотря на наличие рассмотренного выше достаточно точного метода сум­мирования погрешностей, на практике очень часто встречается потребность в исполь­зовании быстрых, приближенных методов определения суммарной погрешности, когда недостаток времени или исходных данных не позволяет использовать точный метод. В этих случаях пренебрегают частью тех правил суммирования погрешностей, которые выше были изложены, и прибегают к заведомо нестрогим, упрощенным методам. В этой связи полезно четко отдавать себе отчет в том, к каким ошибкам при­водит несоблюдение того или иного требования правил суммирования.

Для этого рассмотрим упрощенные варианты расчета, используя данные при­веденного выше примера суммирования составляющих погрешности. Одним из та­ких упрощений может быть использование приближенного соотношения V₀,9 ~ 1»6а для большого класса высокоэнтропийных распределений. В этом случае каждой из составляющих также должен быть приписан определенный закон распределения и определены значения о,-, путем суммирования которых находятся значения а_ш а_м и а_к. Однако далее композиции и их энтропийные коэффициенты не определя­ются, а 7н и у_к находятся как 7₀,о = 1,6а. В нашем примере это даст

Yo.tm = 1,6а_н = 1,6 . 0,207 = 0,33%; _То,₉к = 1,6а_к = 1,6 • 0,36 = 0,58%.

Если результирующее распределение близко к нормальному, то подобным же образом может быть определена погрешность не только с Р_д = 0,9, но и с Р_д = 0,95 согласно соотношениям:

Yo,95h== 1,9ба_н = 1,96-0,207=0,4%; <Уо,95к= 1,96а_к = 1,96 . 0,36 = 0,7%.

При_назначении 25%-ного запаса на старение и округлении нормируемых зна­чений 7н и у_к в соответствии с ГОСТ 8.401—80 и тот и другой путь в нашем при­мере приведут к одним и тем же нормируемым значениям 1,0 и 0,5.

Наиболее трудоемкими при подобных расчетах являются назначение законов распределения составляющих и расчет о_г-. При крайней нехватке времени или ис­ходных данных можно пойти на то, чтобы считать для всех составляющих соотно­шение между максимальным значением погрешности и с. к. о. постоянной вели­чиной и вычислять Ye по формуле

УХт^УЩ^г-

В нашем примере (у_кт = 0,15%, Тук т = 0,4%, у_ет = 0,15% и y_Um = 0,7%) такой расчет привел бы к

Та ⁼ 1/~Удт НЬ Уукт=V 0,15^s + 0,4^г=0,43%;

Ук^У^т+У^т+Увт+УЬт - ^0,15² + 0,4^+0,15^+0,?Т_{= 0},8₃₎

т. е. погрешность прибора с 25%-ным запасом на старение чуть-чуть бы не уложи­лась в нормируемые значения 1,0 и 0,5 и прибор надо было бы отнести к классу 1,5/1,0. Однако неточность такого приближенного расчета, как видно из приведенных цифр, не столь велика, и при необходимости и соответствующих оговорках в неответствен­ных случаях такой метод может широко использоваться.

Что же касается пренебрежения учетом корреляционных связей и использо­вания арифметического суммирования всех составляющих, то это недопустимо во всех случаях, так как может привести к тому, что будут складываться те погрешности, которые в действительности вычитаются друг из друга, и результат будет суще­ственно завышен. Так, в нашем примере сумма всех составляющих равна 0,15 + + 0,5+0,45+0,7= 1,8% и прибор будет ошибочно отнесен к классу 2,5.

ГЛАВА ВТОРАЯ

Динамические свойства измерительных преобразователей

2-1. ДИНАМИЧЕСКИЕ СВОЙСТВА ПРЕОБРАЗОВАТЕЛЕЙ С ТЕПЛОВОЙ ИНЕРЦИОННОСТЬЮ

Необходимость в решении задачи о тепловой инерционности чаще всего возникает в двух случаях, схематически изображенных на рис. 2-1. В первом случае (рис. 2-1, а) датчик, имеющий массу т и удельную теплоемкость с и находящийся в среде с постоянной темпе­ратурой ©_х, в некоторый момент времени t_± включается в работу.

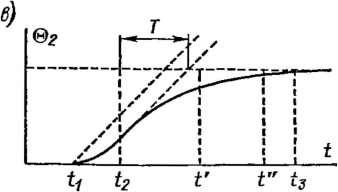
Рис. 2-1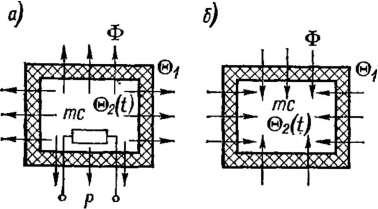

В результате этого внутри его начинает выделяться мощность Р и температура датчика в₂ (£) начинает нарастать, стремясь к некоторому установившемуся значению. Приближенное уравнение преобразова­ния

или, приводя его к табличной форме, получим

где 5 — поверхность теплообмена, называемая также поверхностью охлаждения преобразователя; g — коэффициент теплоотдачи.

Приведенное уравнение соответствует уравнению апериодического звена PS₀ = (©₂ — ©_х) + Td (©₂ — © J/d/. Статическая чувствитель­ность преобразователя S₀ = (©₂ — ©J/P = 1/(£S), постоянная вре­мени Т = mc! (£S).

Во втором случае (рис. 2-1, б) прибор или датчик с массой т и теп­лоемкостью с, имеющий температуру ©₂, ^в момент времени t₁ поме­щается в среду с температурой @_ь и в результате теплообмена со сре­дой его температура начинает стремиться к значению в_х. Уравнение

преобразования ь этом случае

а ^ I ^{тс d@}2

или в операторной форме ©₂ = O^l + Тр).

На рис. 2-1, в показана экспериментальная кривая переходного процесса теплового преобразователя. Отличие этой кривой от типовой кривой переходного процесса апериодического преобразователя за­ключается в том, что на участке t₂ — t_x имеет место так называемый дорегулярный режим (не учтенный при выводе вышеприведенных уравнений), объясняемый тем, что за это время происходит перерас­пределение температур в толще самого тела и установление градиен­тов температуры, соответствующих однонаправленному тепловому потоку. На участке t₃ — протекает так называемый регулярный ре­жим установления температуры, а после t₃ наступает установившийся режим теплового равновесия. В измерительных преобразователях дорегулярный режим чаще всего занимает относительно малое время, поэтому для оценки динамических свойств преобразователя применимы все расчетные соотношения, полученные для апериодического преобра­зователя.

Следует обратить внимание на то обстоятельство, что тепловая постоянная времени Т = mc /(£S) определяется полной теплоемкостью преобразователя и условиями его теплообмена с окружающей средой, поэтому один и тот же преобразователь имеет разные постоянные вре­мени в зависимости от условий теплообмена.

Для расчета постоянной времени необходимо найти общую тепло­емкость деталей прибора или датчика, что может быть выполнено весьма приближенно. Так, для всех тяжелых металлов (медь, латунь, железо) можно принимать с = 400 Дж/(кг-К), для более легких ма­териалов (алюминий, фарфор, слюда) с = 800 Дж/(кг-К), а для органических материалов (текстолит, гетинакс, оргстекло) с =

= 1300 Дж/(кг-К).

Коэффициент теплоотдачи зависит от среды, в которой находится преобразователь, от состояния его поверхности, от конвекции газа или жидкости вокруг него (см. § 11-1) и лишь приближенно поддается расчету. Ниже приведены экспериментально полученные значения £ в ваттах на квадратный метр-кельвин для некоторых типичных дета­лей:

„ « j/".-i 1, 13

/ уd м У 1) 14

-в) 146

д 166

Vl 1 11 178

Rr _ \f 2 V \Г2 ■ 2,0 249

^ -(0,1 4-1,5) со- 280

Еш-чГ™ hKreOMy, 284

а) 1 xl 310

/ = у J [^sin(— + cpJJ = (12-2) 348

0,8 1,2 1,6 мкм 367

СПИСОК ЛИТЕРАТУРЫ 382

1 т —

^m ]/(1 ___4jt2.2002 . 5 • ю-12. 1. 104)2+4^2.2002 • 25 • 10-24(0,31. 10⁶4-200. №*

= Р_1т ¹ ^ 1,09Р_1га.

|А(1 —0,08)2+0,0004

Пример 2. Оценим динамические свойства тензорезиставного датчика дав­ления (рис. 2-4), представляющего собой закрепленную в титановую втулку / сап­фировую мембрану с выращенными на ней кремниевыми тензорезисторами

см. § 5-5). Давление подается в подмембранную камеру через штуцер 2, который служит я для крепления датчика к объекту измерения. В качестве дополнительного элемента крепления может быть использован уголь­ник 3.

Динамическая чувствительность датчика может быть определена как

S(p)^=S_l (р) S₂(p) K_sS₄ (pi

где Si (р) — коэффициент преобразования измеряе­мого давления Р_изм в давление в подмембранной камере. Р_х; S₂ (р) — коэффициент преобразования давления Р_х в деформацию мембраны; К_я — коэф­фициент преобразования деформации е в напряжение на выходе теизомоста и S₄ (р) — коэффициент усиле­ния усилителя, размещаемого в верхней части кор­пуса датчика.

Частота собственных колебаний мембраны при тол­щине 2,25 мм и диаметре 12 мм составляет 33 кГц. По­лоса пропускания усилителя, очевидно, может быть значительно выше. Таким образом, видимо, наиболее инерционным является канал передачи давления. Пусть длина штуцера /_тр = .55 мм, диаметр канала d = 4 мм, объем подмем­бранной камеры V =? 480 мм®.

^{1 1} _глог с ⁵тр'тр. вкв _в

2л УLC

г , ЭКВ

t—L_Tp~p— — скорость звука в газе; р ■

-, где С = + = —₂-

Собственная частота канала /₀ = ■

рс^{2 1} рс² " плотность газа; 5_тр — 3td²/4 —

сечение трубки; /_Тр._ЭКв ^тр — эквивалентная длина трубки. Таким образом^ собственная частота канала

1

/о-

2л Vkl_Tp{kl_Tv^V/S_rp)

В том случае, если объем камеры относительно велик, т. е. V/S_Tp >> 1_тр, то коэф­фициент ft — 1; если У/5_тр < /_тр, то собственная частота трубки /_тр — с/ (4/_тр), т. е. коэффициент k = 2/я. В данном случае WS_xp = 40 мм, /_хр — 55 мм. Таким образом, коэффициент k лежит в- диапазоне k — 1 0,65, приближенно можно счи­тать k = 0,8. При давлении Р = 10^ Па скорость звука в воздухе с = 334 м/с и собственная частота

_t I 334 _fi7nr

fo = =i=870 Гц.

2л /0,8 • 55 (0,8 • 55 + 40) 10-е

Таким образом, датчик может быть использован для измерения переменной составляющей пульсирующих давлений при частоте пульсаций, значительно мень­шей 900 Гц. Погрешность измерения переменной составляющей y_f ж (//870)².

2-3. РАСЧЕТ ЧАСТОТНЫХ ХАРАКТЕРИСТИК МЕХАНИЧЕСКИХ И АКУСТИЧЕСКИХ ЗВЕНЬЕВ С СОСРЕДОТОЧЕННЫМИ И РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

Рнс. 2-4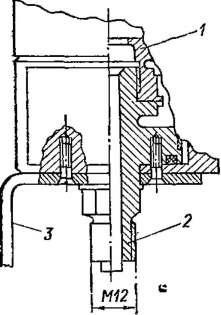

Для построения частотной характеристики колебательного звена второго порядка необходимо и достаточно знать собственную частоту со₀ (или соответствующий ей период Г₀) и коэффициент, характери­зующий потери энергии в системе. В практических расчетах измери­тельных преобразователей потери энергии обычно характеризуются степенью успокоения (3 или добротностью Q. Однако встречаются и другие показатели потерь: d — затухание контура, б — декремент

затухающих колебаний, h — коэффициент затухания, с*¹. Все пере­численные показатели однозначно связаны между собой, и их соотно­шения имеют вид

Р = 1/(2Q) = d/2 = 6/сОо = Н/(2а>о)\ Q= 1/(2Р) = о>₀/(26) = а>₀//г.

Значения Q или р, как правило, не поддаются точному расчету, однако они сохраняются постоянными для однотипных систем и по­этому могут быть установлены заранее на основе предыдущего опыта. Так, известно, что добротность электрических LC-контуров на низких звуковых частотах (50—500 Гц) составляет 10, а для высокочастотных контуров (на радиочастотах) не превосходит 200.

а при вращательном движении

Внутреннее трение в металлах ограничивает степень успокоения механических резонансных систем (не имеющих специальных успо­коителей) обычно значениями р — 0,06 0,04, а их добротность, сле­довательно, составляет Q = 8 -з- 12.

Рис 2-5 .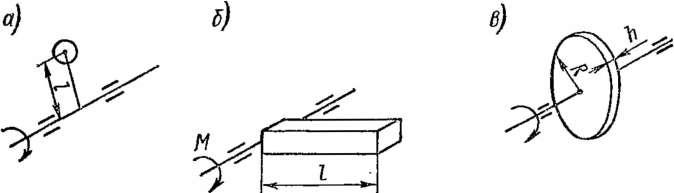

Значения собственной частоты механических систем, наоборот, могут быть весьма разнообразны (например, от долей герца до 50 кГц — см. § 4-4) и поэтому всегда должны рассчитываться. Основными форму­лами для расчета собственной частоты при поступательном движении являются

где т — масса системы, кг; W — жесткость, Н./м; п — податливость, м/Н; М — удельный устанавливающий момент, Н-м (на 1 радиан); J — момент инерции, кг-м².

Момент инерции J для конструкций, совершающих крутильные колебания и представленных на рис. 2-5, а, б, е, определяется сле­дующими соотношениями: J = ml²; / = т (/./]/З)²; / = т (/?/К²)². Вопросы расчета податливостей и жесткостей упругих элементов рас- личных видов подробно рассмотрены ниже, в главе четвертой.

Расчет собственной частоты звена с сосредоточенными параметрами покажем на примере расчета собственной частоты акселерометра с тензорезисторами (рис. 2-6, а). Представляя упругий элемент акселе­

рометра как балку длиной шириной b и толщиной h, определим ее

41³

податливость (см. § 4-2) как = ^и собственную частоту как

/о = - -7:— = — -7-1/ — • Однако подобный расчет является весь- 2л}/ тп Ал I г ml

151

So

Рис. 2-6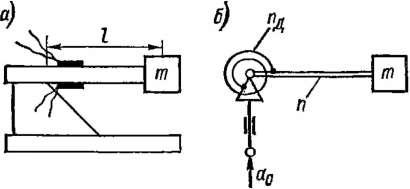

ма приближенным. Фактором, который может вызвать отклонение частотной характеристики датчика от рассчитанной, является неучтен­ная податливость в месте заделки неподвижного конца упругого эле­мента в основание. Если изобразить механическую схему датчика с учетом этой податливости я_д, как это показано на рис. 2-6, б, то становится ясно, что податливости п и п_д суммируются и собственная частота оказывается ниже рассчитанной. Вторым фактором, вызываю­щим отклонение собственной частоты от рассчитанной, является то обстоятельство, что в любой реальной конструкции упругий элемент и закрепленная на нем масса имеют конечные размеры. Рассматривая систему с сосредоточенными параметрами, предполагаем, что упругий

w_1pw_n W_2p U)

элемент — балка —имеет пренебрежимо малую массу по сравнению с массой т, а масса т имеет пренебрежимо малые размеры по сравне­нию с размерами балки, т. е. является материальной точкой.

Отступление от этих условий приводит к весьма существенному из­менению частотной характеристики, так как в системе появляются ре- зонансы на двух частотах (рис. 2-6, е) и частота первого из них ока­зывается ниже рассчитанной выше. В частности, если инерционную массу представить в виде цилиндра радиусом R — / У 2/3 0,82/, где I — длина балки, то частота (o_ip = 0,73со₀, а со_2р = 2,7со₀.

Собственная частота столба газа, заключенного в трубе с жесткими стенками и представляющего собой резонатор с равномерно распреде­ленной по длине / массой и жесткостью, определяется скоростью рас­пространения возмущения, т. е. скоростью звука в среде, заполняю­щей резонатор, и длиной последнего.

Скорость звука в газе определяется соотношением

• с = ]/£>ву/М=УуР1р>

где R —универсальная газовая постоянная, равная 8,314 Дж./(моль- К); в — абсолютная температура, К; Y ^{= c}p!°v — отношение теплоемко- стей при постоянном давлении и постоянном объеме; М — молеку­лярная масса газа; Р — давление газа, Па; р — плотность газа, кг/м³.

вость ft, также равную податливости этого стержня, была бы равна

* ^ * _ J_ l/Ж ₌ _L l/Z

^/0 2л У т/г 2л У Slpl 2л1 V р*

Отсюда действительное значение собственной частоты заделанного стержня может быть выражено через его полные массу т и податли­вость ft как

f Л V, Л 1 1 1

То = — / о =

2 2 2пУтп _п -,/~4 2я 1/"0,405тгс "

У tf? ^тП

Различие частот /₀ и /о обусловлено тем, что нижний торец стержня (рис. 2-7) не совершает колебаний и поэтому в колебаниях участвует не вся масса стержня, а лишь некоторая ее часть. Отсюда произведе­ние 0,4т, входящее в формулу для /₀, можно трактовать как некоторую эквивалентную массу т_экв — 0,4т, используя значение которой, соб­ственную частоту стержня можно определить по обычной формуле

/о — ~

„ 2л у т_экпп

Аналогично этому можно говорить и об эквивалентной податливо­сти п_экв — 0,4п, ибо верхний конец стержня (рис. 2-7, а) не испыты­вает при колебаниях сжатия и растяжения, в которых участвует лишь нижняя часть стержня. С использованием значения п_экв собственная частота равна

_{fu =} * ⁰ 2л Утп_экв

Поэтому в общем виде можно считать, что собственная частота всегда может быть найдена как

экв^экв

fo-

2л Ут,

но в первом случае т_экв — 0,4т, а /г_экв = /г, а во втором т_экв — т, а п_экп = 0,4/г.

Подобные эквивалентные параметры могут быть найдены и для дру­гих колебательных систем. Например, для мембраны на рис. 2-8, а, заделанной по контуру (если в качестве /г_экв принять податливость ее центра), т_т 0,32т. Для балки, лежащей на двух шарнирных опорах, т_экв = 0,485т, а при заделанных концах т_экв = 0,371т при расчете их податливости для центра балки. Для консольной балки постоянного сечения т_жв = 0,236т, а для балки равного сопротивле­ния т_экв = 0,067т при использовании в расчете податливости сво­бодного конца балки. Для натянутой ленты (см. рис. 4-3, в) при ис­пользовании податливости от силы по ее центру, как и для стержня, ^тжв — (4/эх²)т = 0,405т.

Такая эквивалентная замена позволяет достаточно просто полу­чить расчетные формулы для собственной частоты разнообразных и достаточно сложных конструкций преобразователей. Так, например,

преобразователь пьезоэлектрического акселерометра (рис. 2-8, 6) со­стоит из инерционной массы 1, пластин пьезокерамики 2 и основания 3, соединенных между собой клеем или пайкой. Благодаря тому что модуль упругости керамики близок к модулю металлов, детали 1 и 2 можно рассматривать как единый стержень длиной I с эквивалентной массой, равной массе стержня т_ст, и эквивалентной податли­востью, равной 0,4 податливо­сти всего стержня п_ст. Основа­ние 3 можно рассматривать как мембрану, заделанную по кон­туру и нагруженную в центре массой стержня.

Рис. 2-8

Так как в колебаниях всей системы масса стержня участвует полностью, а масса мембраны — лишь частично, то эквивалентная масса всей системы т_жв = т_СТ + -}- 0,32m_OCH. Податливость же мембраны, наоборот, используется полностью, в то время как податливость стержня участвует лишь частично. Поэтому эквивалентная податливость системы п_экв — п_0сн + + 0,4п_сг. Отсюда собственная частота всей системы равна

2п V*n_BKBn_aKB 2jt]/(m_CT + 0,32m_OCII) (д_осн + 0,4/1_Ст) °

2-4. ЭКВИВАЛЕНТНЫЕ ЭЛЕКТРИЧЕСКИЕ СХЕМЫ МЕХАНО-ЭЛЕКТРИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ

В измерительной технике часто используются такие преобразова­тели, частотные характеристики которых определяются частично электрическими, а частично механическими (или акустическими) пара­метрами. В подобных случаях удобнее все параметры привести" к ка­кому-то единому (лучше электрическому) виду и весь преобразова­тель изобразить в виде некоторой эквивалентной (т. е. обладающей теми же частотными свойствами) электрической цепи, которая отра­зила бы как электрические, так и механические элементы. Это может быть достигнуто методом, который получил название метода эквива­лентных схем или электрических схем замещения и основывается на общности дифференциальных уравнений электрических и механиче­ских систем.

HIII 0		f
	^
£ ^

На рис. 2-9 показаны механическая колебательная система и ее электрический аналог в виде последовательного и параллельного кон­туров.

или в виде

Дифференциальное уравнение механической системы может быть записано в виде

_m^ ₊ Pv+n §vdt-F, (2-2)

где г — приложенная сила; т — масса подвижной части; Р — коэф­фициент успокоения, характеризующий вязкое трение; п — податли­вость пружины; х — перемещение подвижной части; v — dx/dt — ско­рость движения подвижной части.

У////////////////Л

'////////////////%

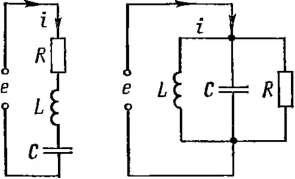
_й Рис. 2-9

Дифференциальное уравнение последовательного контура может быть записано в виде

_г d²q . _D dq , 1

(2-3)

dt²

Дифференциальное уравнение параллельного контура

(2-4)

Сравнение дифференциальных уравнений (2-1), (2-3) и (2-2), (2-4) показывает, что механическая система может быть заменена как после­довательным, так и параллельным электрическим контуром. В табл. 2-2 представлены электрические аналоги механических параметров для того и другого контура.

Таблица 2-2

Механическая величина	Электрическая величина
	последовательного контура	параллельного контура
Сила F Скорость V Перемещение х Количество движения р Коэффициент успокое­ния Р Масса т Податливость п	ЭДС е Ток i Заряд q Магнитный поток Ф Сопротивление R Индуктивность L Емкость С	Ток i ЭДС е Магнитный поток Ф Заряд q Проводимость 1 /R Емкость С Индуктивность L

Метод электромеханических аналогий широко применяется при расчете измерительных преобразователей (см., например, работу [2]). Для сопоставления эквивалентной схемы нужно выбрать электрический аналог механической системы и определить коэффициент электроме­ханической связи равный к_ш = Flv = —Hv для последователь-

Составляющая силы, имеющая частоту со, определяется как = и коэффициент электромеханической связи

_{где Со} — емкость преобразователя; Е — напря­женность постоянного электростатического поля между пластинами.

Ри

Рис. 3-1

Эквивалентная схема преобразователя с трансформатором пред­ставлена на рис. 2-12, б и без трансформатора — на рис. 2-12, в.