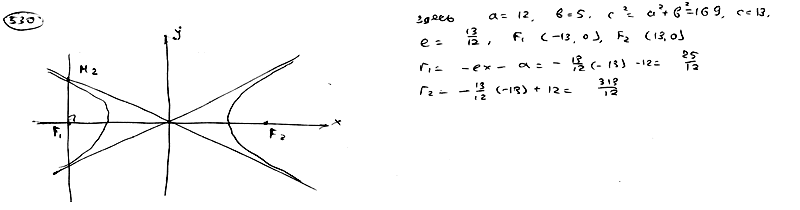Глава 19. Гипербола

515

Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:

515.1

ее оси 2a=10 и 2b=8;

515.2

расстояние между фокусами 2c=10 и ось 2b=8;

515.3

расстояние между фокусами 2c=6 и эксцентриситет e=3/2;

515.4

ось 2a=16 и эксцентриситет e=5/4;

515.5

уравнения асимптот и расстояние между фокусами 2c=20;

515.6

расстояние между директрисами равно 228/13 и расстояние между фокусами 2c=26;

515.7

расстояние между директрисами равно 32/5 и ось 2b=6;

515.8

расстояние между директрисами равно 8/3 и эксцентриситет e=3/2;

515.9

уравнения асимптот и расстояние между директрисами равно 64/5;

516

Составить уравнение гиперболы, фокусы которого расположены на оси ординат симметрично относительно начала координат, зная, кроме того, что:

516.1

ее полуоси a=6, b=18 (буквой а мы обозначаем полуось гиперболы, расположенной на оси абсцисс);

516.2

расстояние между фокусами 2с=10 и эксцентриситет e=5/3;

516.3

уравнения асимптот и расстояние между вершинами равно 48;

516.4

расстояние между директрисами равно 50/7 и эксценриситет e=7/5;

516.5

уравнения асимптот и расстояние между директрисами равно 32/5.

517

Определить полуоси а и b каждой из следующих гипербол:

517.1

;

517.2

;

517.3

;

517.4

;

517.5

 ;

517.6

;

517.7

.

518

Дана гипербола . Найти: полуоси а и b, фокусы, эксцентриситет, уравнения асимптот, уравнения директрис.

519

Дана гипербола . Найти: полуоси а и b, фокусы, эксцентриситет, уравнения асимптот, уравнения директрис.

520

Вычислить площадь треугольника, образованного асимптотами гиперболы и прямой .

521

Установить, какие линии определяются следующими уравнениями. Изобразить эти линии на чертеже.

521.1

 ;

521.2

;

521.3

 ;

521.4

.

522

Дана точка M₁(10; ) на гиперболе . Составить уравнения прямых, на которых лежат фокальные радиусы точки М₁.

523

Убедившись, что точка М₁(-5; 9/4) лежит на гиперболе , определить фокальные радиусы точки М₁.

524

Эксцентриситет гиперболы e=2, фокальный радиус ее точки М, проведенный из некоторого фокуса, равен 16.

Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.

525

Эксцентриситет гиперболы e=3, расстояние от точки М гиперболы до директрисы e=3, расстояние от точки М гиперболы до директрисы равно 4. Вычислить расстояние от точки М до фокуса, одностороннего с этой директрисой.

526

Эксцентриситет гиперболы e=2, центр ее лежит в начале координат, один из фокусов F(12; 0). Вычислить расстояние от точки М₁ гиперболы с абсциссой, равной 13, до директрисы, соответствующей заданному фокусу.

527

Эксцентриситет гиперболы e=3/2, центр ее лежит в начале координат, одна из директрис дана уравнением x=-8. Вычислить расстояние от точки М₁ гиперболы с абсциссой, равной 10, до фокуса, соответствующего заданной директрисе.

528

Определить точки гиперболы , расстояние от которых до правого фокуса равно 4,5.

529

Определить точки гиперболы , расстояние которых до левого фокуса равно 7.

530

Через левый фокус гиперболы проведен перпендикуляр к ее оси, содержащей вершины. Определить расстояние от фокусов до точек пересечения этого перпендикуляра с гиперболой.

531

Пользуясь одним циркулем, построить фокусы гиперболы (считая, что оси координат изображены и масштабная единица задана).

532

Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично относительно начала координат, если даны:

532.1

точки M₁(6; -1), M₂(-8; ) гиперболы;

532.2

точка М₁(-5; 3) гиперболы и эксцентриситет e=;

532.3

точка М₁(9/2; -1) гиперболы с уравнения асимптот ;

532.4

точка М₁(-3; 5/2) гиперболы и уравнения директрис ;

532.5

уравнения асимптот и уравнения директрис .

533

Определить эксцентриситет равносторонней гиперболы.

534

Определить эксцентриситет гиперболы, если отрезок между ее вершинами виден из фокусов сопряженной гиперболы под углом 60⁰.

535

Фокусы гиперболы совпадают с фокусами эллипса . Составить уравнение гиперболы, если ее эксцентриситет e=2.

536

Составить уравнение гиперболы, фокусы которой лежат в вершинах эллипса , а директрисы проходят через фокусы этого эллипса.

537

Доказать, что расстояние от фокуса гиперболы до ее асимптоты равно b.

538

Доказать, что произведение расстояний от любой точки гиперболы до двух ее асимптот есть величина постоянная, равная .

539

Доказать, что площадь параллелограмма, ограниченного асимптотами гиперболы и прямыми, проведенными через любую ее точку параллельно асимптотами, есть величина постоянная, равная ab/2.

540

Составить уравнение гиперболы, если известны ее полуоси a и b, центр C(x₀; y₀) и фокусы расположены на прямой:

540.1

параллельной оси Ox;

540.2

параллельной оси Oy.

541

Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис:

541.1

 ;

541.2

;

541.3

.

542

Установить, какие линии определяются следующими уравнениями. Изобразить эти линии на чертеже.

542.1

;

542.2

;

542.3

;

542.4

.

543

Составить уравнение гиперболы, зная, что:

543.1

расстояние между ее вершинами равно 24 и фокусы суть F₁(-10; 2), F₂(16; 2);

543.2

фокусы суть F₁(3; 4), F₂(-3; -4) и расстояние между директрисами равно 3,6;

543.3

угол между асимптотами равен 90⁰ и фокусы суть F₁(4; -4), F₂(-2; 2).

544

Составить уравнение гиперболы, если известны ее эксцентриситет e=5/4, фокус F(5; 0) и уравнение соответствующей директрисы .

545

Составить уравнение гиперболы, если известны ее эксцентриситет e=13/12, фокус F(0; 13) и уравнение соответствующей директирсы .

546

Точка А(-3; -5) лежит на гиперболе, фокус которой F(-2; -3), а соответствующая директриса дана уравнением . Составить уравнение этой гиперболы.

547

Составить уравнение гиперболы, если известны ее эксцентриситет e=, фокус F(2; -3) и уравнение соответствующей директрисы .

548

Точка М₁(1; -2) лежит на гиперболе, фокус которой F(-2; 2), а соответстующая директриса дана уравнением . Составить уравнение этой гиперболы.

549

Дано уравнение равносторонней гиперболы . Найти ее уравнение в новой системе, приняв за оси координат ее асимптоты.

550

Установив, что каждое из следующих уравнений определяет гиперболу, найти для каждой из них центр, полуоси, уравнения асимптот и построить их на чертеже:

550.1

;

550.2

 ;

550.3

.

551

Найти точку пересечения прямой и гиперболы .

552

Найти точки пересечения прямой и гиперболы .

553

Найти точки пересечения прямой и гиперболы .

554

В следующих случаях определить, как расположена прямая относительно гиперболы: пересекает ли, касается или проходит вне ее:

554.1

 , ;

554.2

, ;

554.3

, .

555

Определить, при каких значениях m прямая :

555.1

пересекает гиперболу :

555.2

касается ее;

555.3

проходит вне этой гиперболы.

556

Вывести условие, при котором прямая касается гиперболы .

557

Составить уравнение касательной к гиперболе в ее точке M₁(x₁; y₁).

558

Доказать, что касательные к гипербле, проведенные в концах одного и того же диаметра, параллельны.

559

Составить уравнения касательных к гиперболе , перпендикулярных к прямой .

560

Составить уравнения касательных к гиперболе , параллельных прямой .

561

Провести касательные к гиперболе параллельно прямой и вычислить расстояние d между ними.

562

На гиперболе найти точку М₁, ближайшую к прямой , и вычислить расстояние d от точки М₁ до этой прямой.

563

Составить уравнение касательной к гиперболе , проведенных из точки А(-1; -7).

564

Из точки С(1; -10) проведены касательные к гиперболе . Составить уравнение хорды, соединяющей точки касания.

565

Из точки Р(1; -5) проведены касательные к гиперболе . Вычислить расстояние d от точки Р до хорды гиперболы, соединяющей точки касания.

566

Гипербола проходит через точку А(; 3) и касается прямой . Составить уравнение этой гиперболы при условии, что ее оси совпадают с осями координат.

567

Составить уравнение гиперболы, касающейся прямых , , при условии, что ее оси совпадают с осями координат.

568

Убедившись, что точки пересечения эллипса и гиперболы являются вершинами прямоугольника, составить уравнения его сторон.

569

Даны гиперболы и какая-нибудь ее касательная, Р – точка пересечения касательной с осью Ох, Q – проекция точки касания на ту же ось. Доказать, что .

570

Доказать, что фокусы гиперболы расположены по разные стороны от любой ее касательной.

571

Доказать, что произведение расстояний от фокусов до любой касательной к гиперболе есть величина постоянная, равная b².

572

Прямая касается гиперболы, фокусы которой находятся в точках F₁(-3; 0), F₂(3; 0). Составить уравнение этой гиперболы.

573

Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, если известны уравнение касательной к гиперболе и расстояние между ее вершинами 2а=8.

574

Доказать, что прямая, касающаяся гиперболы в некоторой точке М, составляет равные углы с фокальными радиусами F₁M, F₂M и проходит внутри угла F₁MF₂.

575

Из правого фокусы гиперболы под углом (<<) к оси Ох направлен луч света. Известно, что . Дойдя до гиперболы, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.

576

Доказать, что эллипс и гипербола, имеющие общие фокусы, пересекаются под прямым углом.

577

Коэффициент равномерного сжатия плоскости к оси Ох равен 4/3. Определить уравнение линии, в котороую при этом сжатии преобразуется гипербола .

578

Коэффициент равномерного сжатия плоскости к оси Оу равен 4/5. Определить уравнение линии, в которую при этом сжатии преобразуется гипербола .

579

Найти уравнение линии, в которую преобразуется гипербола при двух последовательных равноменых сжатиях плоскости к координатным осям, если коэффициенты равномерного сжатия плоскости к осям Ох и Оу соответствуют 2/3 и 5/3.

580

Определить коэффициент q равномерного сжатия плоскости к оси Ох, при котором гипербола преобразуется в гиперболу .

581

Определить коэффициент q равномерного сжатия плоскости к оси Оу, при котором гипербола преобразуется в гиперболу .

582

Определить коэффициенты q₁, q₂ двух последовательных равномерных сжатий плоскости к осям Ох и Оу, при которых гипербола преобразуется в гиперболу .